Table of Contents
浮動小数点表示の考え方
コンピュータが直接扱うことのできるデータは, 0 と 1 を有限個並べて表現する 2 進数ですが, 小数の形式で表現される数については一般的には浮動小数点数という形式で記憶されてます.
この浮動小数点数を理解するためには, まず単純な固定小数点を理解する必要があるので先に解説します.
固定小数点数(Fixed-point arithmetic)

n bit与えられた時, $i$ bitと $i-1$ bitの間に小数点が固定されているとして数値を表現する方法です.
signed intの場合は 小数点が第 0 ビットの右側にある (固定されている) 固定小数点の特殊な場合と考えることが出来ます.
この固定された小数点の位置のことを binary point と呼んだりします.
メリット
- 浮動小数点数にくらべ高速に計算できる
デメリット
- 浮動小数点数に比べて表現できる値の範囲ははるかに狭いため, 算術オーバーフローや算術アンダーフロー, 丸め誤差が発生しやすい
たとえば、2 進小数点の右側が 4 ビットの固定小数点の表現は, 精度が $2^{-4}$, つまり最下位ビットの値になります. これ以下の数値については表現することが出来ず丸め誤差が発生してしまいます.
練習問題
Problem 1: 基本情報技術者試験平成18年秋期 問5
負数を2の補数で表す16ビットの符号付き固定小数点数の最小値を表すビット列を,16進数として表せ
解答
2の補数で表す16ビットの符号付き固定小数点数の最小値はbinary pointの位置に関わらず
1
1000 0000 0000 0000
従って, これを16進数変換すると 8000
解答終了
Problem 2: 固定小数点による表示
10進数-5.625を, 8ビット固定小数点形式による2進数で表しなさい. ここで, 小数点位置は3ビット目と4ビット目の間とし, 負数には2の補数表現を用いる

解答
$5.625$ を8ビット固定小数点形式にて2進数表現すると0101.1010.
今回は2の補数表現を用いているので, $-5.625$は
1
2
3
(1): 0101.1010
(2): 1010.0101 #反転
(3): 1010.0110 #プラス1
従って, 1010.0110
解答終了
Problem 3: 固定小数点の表示範囲
8 ビットで2の補数表示の固定小数点表示したとき、小数点が第 4 ビットと第 3 ビットの間にあると仮 定します. この条件で表される数値を$x$としたとき, 最大値と最小値を求めなさい.
解答
- 最小:
1000 0000 - 最大:
0111 1111
なので, $x \in [-8, 7.9375]$
解答終了
浮動小数点数
浮動小数点数は固定小数点表示に比べ非常に大きな数や非常に小さな数を表示するのに適しています. データ型「倍精度浮動小数点」(64 bit)と「単精度浮動小数点」(32 bit)の二つがある(C言語ではdouble, floatがそれぞれに対応している)が表示構造としてはどちらも基本的なところは同じで
\[(-1)^S \times M \times B^E\]- S: 符号
- M: 仮数部(mantissa)
- E: 指数部(exponent)
- B: 底(base)

具体的実装方式としては, 代表的なものとして「IBM方式」と「IEEE方式(IEEE 754方式)」があります.
IBM 方式
底を16という特徴があります. 表示される数は単精度に基づく場合
\[(-1)^{S} \times 16^{E-64} \times M\]| 符号部 | 正負を表す |
| 指数部 | 16を基数とし +64 のバイアス表現 |
| 仮数部 | 1未満 0 以上の2進数 |
IBM 方式の浮動小数点の仮数部と指数部のbit数は単精度と倍精度それぞれで以下の通りとなります:
| 単精度 | 倍精度 | |
|---|---|---|
| 符号 | 1 bit | 1 bit |
| 指数部 | 7 bit | 8 bit |
| 仮数部 | 24 bit | 55 bit |
| 合計 | 32 bit | 64 bit |
正規化
Def: 浮動小数点表示における正規化
浮動小数点数が一意かつ有効数字が長くなる(=仮数部を無駄なく使う)ように, 仮数部の上位1 bitを1になるように調整すること
10進小数 0.05 を 2 進小数に変換すると
SS 0.0000 1100 1100 1100 1100 1100…_{(2)} SS
これを仮数部として採用してしまうと, このままだと先頭にならぶ 4 ビットの0が無駄になるってしまいます. ここで正規化を実施すると
\[0.1100 1100 1100 1100 1100 \times 16^{-1}\]と表現されるようになります.
IEEE方式
IEEE方式は「アイ・トリプルイー方式」と読みます. 高精度の数値計算を最適に実行するために米国電気電子技術者協会で提唱した規 格で、現在、多くのワークステーションやパーソナルコンピュータで採用されている方式です.
表示される数は単精度に基づく場合
\[(-1)^{S} \times 2^{E-127} \times (1+M)\]倍精度に基づく場合は
\[(-1)^{S} \times 2^{E-1023} \times (1+M)\]| 符号部 | 正負を表す |
| 指数部 | 2を基数とし +127(単精度) +1023(倍精度) のバイアス表現(=イクセス表現) |
| 仮数部 | 1未満 0 以上の2進数, 1以下の2進小数,正規化され,さらにeconomized form をとる |
| 単精度 | 倍精度 | |
|---|---|---|
| 符号 | 1 bit | 1 bit |
| 指数部 | 8 bit | 11 bit |
| 仮数部 | 23 bit | 52 bit |
| 合計 | 32 bit | 64 bit |
イクセス表現
Def: イクセス表現
nビットで数を表すとき, $2^{n-1}$ を $0$ として、それより上の数を正の数、下の数を負の数とする表示方法をイクセス表現という. 表せる範囲の中央の値を0と見做すことで, 符号ビットを使わずにマイナスの値を表すことが可能となる.
例えば, 4 bitならば0111が 0となります.
IEEE方式におけるeconomized form
Def: Economized form
仮数部は, $1.xxxx$ となるように正規化され, $1$ は省略して $.xxxx$ の部分だけを記憶する表現のことをEconomized formという.
IEEE単精度浮動小数点数の表現範囲
IEEE単精度浮動小数点数における数の表し方の基本は
\[(-1)^{S} \times 2^{E-127} \times (1+M)\]特別な値の表現
非数(NaN)や$\infty$を表す場合を含めると以下のようになります
| 条件 | 表示範囲 |
|---|---|
| $E\in (0, 255)$ | $(-1)^{S} \times 2^{E-127} \times (1+M)$ |
| $E=255, M\neq 0$ | NaN |
| $E=255, M=0$ | $(-1)^S\times \infty$ |
| $E=0, M\neq 0$ | $(-1)^S\times (0.M)_{(2)} \times 2^{-126}$ |
| $E=0, M=0$ | $(-1)^S\times 0$ |
float型で表現し得る数の範囲
| 0より大きい正の最小数 | $1.0 \times 2^{-126}$ |
| 正の最大数 | $1.11\cdots \times 2^{127}$ |
| 0より小さい負の最大数 | $-1.0 \times 2^{-126}$ |
| 負の最小数 | $-1.11\cdots \times 2^{127}$ |
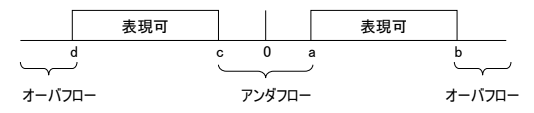
浮動小数点数の問題点
- 仮数部が有限桁しか存在しないため, 「丸め誤差」が発生する
- 指数部も有限桁のため「オーバフロー」と「アンダフロー」の発生
- ほぼ等しい値の浮動小数点数同士の減算の際に, 「桁落ち」が発生するリスクがある
- 小さな数と大きな数の加減算で「情報落ち」が発生するリスクがある
練習問題
Problem: 実数のfloat表現への変換
10進数で表現された$-1$と$1$をIEEE754単精度, float型で表現せよ
解答
$2^{0} \times 1.0 = 1$であるので
1
2
0 01111111 00000000000000000000000
1 01111111 00000000000000000000000
解答終了
Problem: 応用情報技術者平成22年春期 午前問2
以下のような16ビットの浮動小数点形式において,10進数 0.25 を正規化した表現を書け. なお, 正規化は仮数部の最上位桁が1になるように指数部と仮数部を調節する操作とする.
\[-1^S \times M \times 2^{E}\]- S: 符号ビット, 1 bit
- E: 指数部(負の数は2の補数で表現), 4 bit
- M: 仮数部(符号なし2進数), 11 bit
解答
0.25を2進数表現すると0.01となる.
正規化を踏まえると
従って, 0 1111 10000000000が答えとなる.
- S:
0 - E:
1111 - M:
10000000000
解答終了
Appendix: r進数と英語表現
| 2進数 | binary number |
| 8進数 | octal number |
| 10進数 | deciaml number |
| 16進数 | hexadecimal number |
練習問題: 2進数を16進数へ変換
$10101100.01010011$という2進数は, 16進数でいくつか?
解答
$10101100.01010011$を見やすくするため4区分ずつ表すと 1010 1100. 0101 0011.
従って,
従って, $AC.53$ となります.
解答終了
Appendix: NaNとは?
NaN とは 「not a number」を表すnumeric data typeのことです.
直感的には定義できない数を表すnumeric data typeと理解して大丈夫です. 定義できない数の例として
- $0/0$
- $\sqrt{-x} \ $ where $x \geq 0$
- $\log x \ $ where $x < 0$
などがあります.
Column: NaN vs infinity
コンパイラーによって詳細は異なりますが, 計算結果が不定の場合はNaN, 実数演算で最大値を超えるような演算(=オーバーフローを起こすような演算)の実行結果はInfinityとなります.
NaNの倍精度表現
$E=1023, M\neq 0$がNaNを表すので
1
2
1 11111111111 1111111111111111111111111111111111111111111111111111
0 11111111111 1000000000000000000000000000000000000000000000000000
Infinityの倍精度表現
$E=1023, M=0$が$-\infty, \infty$を表すので
1
2
3
4
5
## Infinity
0 11111111111 0000000000000000000000000000000000000000000000000000
## -Infinity
1 11111111111 0000000000000000000000000000000000000000000000000000
References
資格試験
講義ノート
オンラインマテリアル
オンラインツール
(注意:GitHub Accountが必要となります)