Table of Contents
- 1. なぜこの記事をまとめたのか?
- 2. 課題解決の方針
- 3. 課題を理解する
- 4. 解答方針をたてる
- 5. 解答方針に基づき解答実行計画をたてる
- 6. 計画を実行する
- 7. 振り返る
- 8. 問題解決の例
- Appendix
- Rerefences
1. なぜこの記事をまとめたのか?
この記事は G. Polya教授のHow to Solve It(いかにして問題を解くか、柿内賢信訳)を自分なりに振り返り用にまとめたノートです。この本は、数学の問題の解答を読むときに出てくる疑問:
(1) この証明は正しいけど、どうしたらそれを思いつくのだろうか?
(2) この実験はうまくて事実を示しているが、どうしたらこの実験方法を思いつくのか?
このような「数学の問題を解くこと」に関する疑問への答えを「問題を解くとき」の動機や手続きの観点からまとめています。身の回りを振り返ってみると、解答に至るまでのプロセスが詳細に説明されているケースに出会うことは少ないです。一方、データ分析やその他の仕事の場面では、まだ解答が与えられていない問題を解く必要があり、過去問の方法論をマスターしただけでは対応することはできません。そのような場面では「どう解くか?その方法を考える態度」を身につけていることが重要になると考えています。
2. 課題解決の方針
課題解決の進行
- Question: 課題を理解する,何を求めるのか明確にする
- Plan:課題を解く計画を立てる
- Do:計画を実行する
- Review:得られた解のたしからしさを検証する。そして、知識を確立する。
課題解決のステップ
| ステップ | 確認ポイント | |
|---|---|---|
| 1 | Question | (1) 課題を言葉で表現する (2) 課題の全体像を把握する - 課題、各論点、アクションまでのストーリーを意識する - 本質的な選択肢であるか (3) 未知のものは何か,求めたいものはなにか - 与えられているもの(データ)は何か - 条件は何か - 所与のもの/未知のものに名前をつけて整理する (4) 条件を満足させることはできるか,問題は合理的か? - 問題自体に矛盾はないか? (5) 条件は未知のものを定めるのに十分であるか、又は不十分であるか、又は余剰であるか、又は矛盾しているか (6) 明らかにしたいものと与えられたデータ/条件それぞれに記号をつけてそれぞれの関係性を整理 - 条件の各部を分離して、整理する (7) 課題の構造と各論点をわかりやすく説明することはできるか?スラスラ言えるか? |
| 2 | Plan | 解答方針の設定 (1)ゴールからさかのぼってみる (2) 問題を言い換えることができるか? - 定義に戻って言い換えを試みる - 同値変形 (3) 関連した問題は知っているか? - 未知数をよく見て、未知数が同じかまたは似た問題を探す - 未知数が同じかまたは似た問題に関連して役に立ちそうな定理を知っているか考える - 与えられたデータを役立たせるとそれぞれが未知のものの範囲をどのように画定するか類似した問題を手がかりに調べる - 関連した問題を利用するためにうまく補助要素を導入できるか考える (4) まだ問題を解く解答が思いつかないなら、一般的な問題や特殊な問題、類推的な問題を考える (5) 与えられた条件やデータをそのままに未知の対象を変えて、現在直面している問題を解くにあたって役立たせることができる考えるまたは未知のものを固定して、どのような条件とデータがあれば未知のものが定まるか考える (6) 与えられたデータ/条件をすべて使ったか?問題に含まれる本質的な概念はすべて考慮したか?を考える 実行計画の作成 (7)方針と整合的な解答(実行計画)をさだめる (8)「なにを」「いつ」「どこで」「だれが」「どのように」実行するのかを明確に定義する (9) 余計な労働を生み出さない実行計画を作る - Think more, Do less (10) テストケースを事前に定める (11) 進捗管理方針を定める |
| 3 | Do | (1) 解答計画を実行する時、各段階を検討して、その段階が正しいか?考える (2) 当たり前のことを当たり前にやる (3) うまく行く/うまく行かない兆候を見逃さない (4) 計画修正を恐れない |
| 4 | Review | (1) 結果のRobustness check: 同じ結果をちがった仕方で導くことができるか? (2) 得られた結果について、Intuitionを考えて、結果のたしからしさを検証する (3) 得られた結果や方法をなにか別の問題に活かすことはできるか?を考え、知識を深める (4) 解決策の抽象化,モジュール化を実施し、再利用可能性を高める |
課題解決力を身につけるためには?
「問題を解き,疑問を解決し,わかったことをまとめる」方法を身につける練習は、
- 問題を解くというプロセスの真似をする
- 真似を通して得た知識を活用して、問題を自力で解く練習を繰り返す
- 問題解決という活動を習慣として確立する
- 課題解決の各ステップで頻繁に周りの人と相談する
3. 課題を理解する
課題に直面したときはまず、課題の構造を見抜くことに集中します。
なにを解きたいのか明らかにする
未知のものはなにか?与えられているものはなにか?条件はなにか?を明確にします。大学入試等の数学の問題では、何を解くべきなのかは問題文に明確に記載されているので、それを整理するだけで十分です。一方、実世界においては課題解決方法がわからないという体で分析依頼が入ってきますが、その多くはそもそも課題自体が明確に言語化されていない場合が多いです。なのでまず第一歩は、「何が解決すべき課題なのか?」を相手からうまく引き出して合意することが重要です。(→see 対話に臨む際のマインドセット)
例:機械学習をつかっていい感じの成果を出してくれ
「機械学習をつかって企業課題を解決してくれ」という曖昧な指示がクライアントから出たとします。一見、どこから手を出していいかわからないオーダーで途方にくれてしまいそうですが、その背後にある商売の流れ/解決したい事業課題をヒアリングするところから始めるのが重要です。商売の流れを理解することで、その会社が目指す成長計画の障壁はどこにあるのか?どのような課題を解決することでその企業が望む成長を達成することができるか考えることができます。なのでまずヒアリングです。ヒアリングの観点は以下です:
- どのような商品/サービスをどのように売っているのか?
- どのような成長戦略を描いているのか?
- どのような課題に直面しているのか?
- どのような問題/症状になやまされているか?
- 現場から見て、本質的な課題は何か?
このヒアリングと通じて、「どのような課題を解決すべきか?」を明確化し、クライアントと合意します。この段階において、コミュニケーション円滑化の観点から「自分がいままでなにをやってどのような課題を解決してきたのか」「なにができるのか」をクライアントに伝えます。事業課題は多数存在し、またそれをクライアントが認識していない場合もあります。ヒアリングで解決できる解決する価値のある事業課題を聞き出すためには「自分はなにもので,なにができて,他の人とどのように違うのか」を事前に伝えることは有意義です。
次に、「なにをなんのために作るか?」「誰のためになるのか?」という解決方針をクライアントと合意しに行きます。このプロセスを経た後に、具体的に何を作るのか?スケジュール/費用見積もりの話に進みます。解決方針が定まっていないのに具体的な方法論に入ってしまうと、どの具体的な方法が良いのか悪いのかを判断することが難しくなります。最悪手戻りとなる可能性もあるので、一つづつ固められるものは固めていくことは重要です。方針に沿った形で具体的な実行計画候補を複数クライアントに提示し、その中から「世界で最も良い方法」を一緒に探索/合意/実行していきます。その方法が機械学習を用いた方法ならばそれを実施、他に良い方法があるならばそれを実行します。大事なことはあくまでも「事業課題を解決」することです。
局地戦ではなく全体戦で勝つ
物事は「全体」から入らなければなりません。例えば経営においては、会社の基本的方針(経営理念,商品制作,人事政策 .etc)や長期的ビジョンを理解するすることがすべての前提です。常にまず全体を考え、その上で個別の具体策を決めていく。そういう順序で勧めていくことが必要です。如何に優れた具体策でも、全体の方針にあっていなければ、結局は会社にとってマイナスになります。(→see here)
アボカドカッターの罠
眼の前の課題に囚われその課題を解決するためだけのツールを導入することを「アボカドカッターの罠」と呼ぶことがあります. 過去の売上から、将来の売上を予測するモデルや、在庫配分を最適化するAIは一見業務改善における即効性が高そうに見えますが、業務全体のフローの意識することなくその課題にフォーカスしたツールを導入してしまうと、1つの部門の特定のニーズにしか使用できなかったりと、特定の課題しか解決できないことにやがて気づくことになります. データ活用戦略で本当に必要なのは、全体的アプローチです。言うなれば、幅広い用途に使えるナイフです。この点を見誤ると、山積みのテクノロジーを管理するために、多くの不必要なテクノロジーやベンダーを使用するはめに陥ることになり、無形固定資産が積み上がり、管理が大変に成るという自体が発生します. 最悪の場合、誰が何を管理しているかわからず、予算のガバナンスを効かせることができなります.
問題を言葉で表現するときのポイント
「主語」と「動詞」を入れる
主語と動詞を入れた文章にすると、あいまいさが消え、仮説の精度が高まります。日本語は主語を省略する場面が多いので、進めていくうちにメンバーが違うことを考えていたという問題が発生することがあります。これを予防する観点からも「主語」と「動詞」を入れることは有効です。
「Why」より「Where」「What」「How」
- 「Where」: 「どちらか?」「どこを目指すべきか?」
- 「What」: 「何を行うべきか?」「何を避けるべきか?」
- 「How」: 「どう行うべきか?」「どう進めるべきか?」「どれくらいか?(How much)」
「Why = なぜか?」という表現には仮説がなく、何について白黒をはっきりさせようとしているかが明確になっていません。仮説検証するためには問題を「Where」「What」「How」の形で表現することが重要です。
比較表現を入れる
「AかBか」という見極めが必要な問題の場合、「〜はB」というより「Aではなく、むしろB」という表現にする。たとえば、ある新製品開発の方向性が決定すべき課題の場合であれば、「テコ入れすべきは操作性」というより、「テコ入れすべきは、処理能力のようなハードスペックではなく、むしろ操作性」問いしたほうが何と何を対比し、何に答えを出そうとしているのか明確になる。
問題の分類
| 分類 | 明確にすべきこと | 説明 |
|---|---|---|
| 証明問題 | なにが仮定でなにが証明すべき結論か? | 数学的な主張を証明することを目的とする問題を証明問題とよびます。証明問題の主要部分は仮定と結論です。証明問題の多くは,「○○○であるとき×××であることを証明せよ」「○○○ならば×××であることを示せ」という形をしています。この○○○の部分が仮定で,×××の部分が結論です。証明問題の目的は,問題の仮定から結論を導き出す論理的な過程を書き下すことです。 |
| 決定問題 | なにがデータで、なにが条件で、どの未知数を決定すべきかか? | 決定問題とは「未知なるものを決定せよ」ということです。決定問題の主要部分は,データと条件と未知のものです。まず「未知のもの」とは,その決定問題で求めるべきものです。次に「条件」とは,その未知のものに関する条件です。最後に「データ」とは,未知のものと条件によって結びついているもののことです。決定問題の多くは、解を決定せよ,解の個数を決定せよ,体積を決定せよ,そして条件(単に条件といえば必要十分条件のことである)を決定せよ等です。 |
課題の見つけ方
良い課題とは?
良い問題は以下の条件が必要条件となります:
| 必要条件 | 説明 |
|---|---|
本質的な選択肢である |
Actionにつながるか?それに答えが出るとそこから先の検討方向性に大きく影響を与えるか?(→see こちら) |
深い仮説がある |
「常識を覆すような洞察」や「新しい構造の発見」につながるか? |
答えを出せる |
解けない問題を定義しても時間の無駄です(→ see 問題は合理的か?) |
良い課題の見つけるための質問リスト
「この課題が解けるとなぜ嬉しいのか」という質問に答えられるかどうかにかかってきます。以下の質問を尋ねることは有用です:
- 上司や同僚に「この課題が解けるとなぜ嬉しいのか」を伝えられるか実践する
- (1) 何を目指していて, (2) なにがゴールの障壁になっていて, (3) 今回の問題がその障壁の解決にどのようにつながるのかをストーリーで話せるか?(→see here)
- そもそも解けそうか?
- 自分自身にMotivationがあるかないか?
問題は合理的か?
- 条件,仮説は、それが余計なものを含んでいるとき余剰といい、また互いに食い違っている時を矛盾といいます
- 条件,Data,仮説が解を出すにあたって十分か否か?
例1: 矛盾する問題
三角形ABCについて、辺ABの長さは1で、辺BCの長さは2である。そして、角BCAの大きさは45度である。このとき、三角形ABCの面積を求めよ。
この問題は、与えられた条件を満たす三角形がないので存在しない。
\[\begin{aligned} &3x + 2y + z = 10\\ &x + y + z = 6\\ &2y + z = 4\\ \end{aligned}\]例2: 1次独立
と式が与えられたとき、$(x, y, z)$の組を求めよ、という問題が与えられたとする。
この連立方程式は矛盾はないが、三つの式は独立でなく解が決定されません。
記号の導入
問題を理解するにあたってまず考えるべきことは、問題文を数式等の数学用語に翻訳するためにどのような設定をするか、 つまり、何をどにように置くか、です。問題に対して適切に文字を置き, 式に翻訳できれば三分の一は解けたようなものと言われています。(こちら参照)
- 複雑な式のなかから共通の形を見いだし, それを別の文字で置き換える.
- いくつかの式のとる値が等しいとして与えられている条件は, この等しい値を文字で表す.
- 変化する量があればその量を変数で表す. 未知量を求めるときは,方程式として解く.
- 条件が「何々が存在する」とあれば, 存在するものを文字に置き,存在する必要条件を求める.
- 図形を一般性を失わないで, できるだけ単純な式になるように座標平面に置く.
- 考える対象が量の関係なら,変数を導入し, 他の量との関係を調べ,関数形に表す.
- 座標のなかで動きのあるものを, 適当な変数(媒介変数,パラメーター)で表す.
- 自然数 $n$ によって定まる場合の数や確率は $a_n$ など数列におく.そのうえで漸化式を考える.
問題を理解/整理する:文字選びのお作法
問題を理解/整理するにあたって所与のもの/未知のものに名前をつけて管理するのが望ましいとされています。名前をつけるにあたって絶対厳守しなくてはならないルールというのはありませんが、遵守が望ましいお作法はあります。
| ルール | 例 | |
|---|---|---|
| (1) | 違う種類の量を表すときはアルファベットやギリシャ文字のように異なる文字を使う | 三角形の辺をそれぞれa, b, cと表すならば角度はα, β, γと表す。 |
| (2) | 同じ種類の量を表すときは、indexをつけた文字で管理する | 3つの三角形の面積をそれぞれ$S_1, S_2, S_3$で表す |
| (3) | 記号は曖昧であってはならない。同じ問題で同じ記号が違った意味をもつことは許されない | |
| (4) | 覚えやすいものでなればならない | 体積を表す変数はVolumeより$V$を当てるべき |
4. 解答方針をたてる
解答計画をたてるということは
- 解答方針をたてる
- 解答方針に基づき解答実行計画をたてる
という流れになります。
解答の条件
まず解答の定義がわからなければ解答を書くことはできません。解答とは、
前提の下で,求められた内容を決定し,その根拠を示す.
根拠を示すのは論証のそれぞれの段階においても必要であり,解答全体として仮定条件から結論条件を導くことができているか,この両面で確認しなければなりません。例えば確率の問題で「3個のサイコロを振る.和が3の倍数になる確率を求めよ」を解こうとします.このとき
サイコロの目の出方は$6^3$通りあり、そのうち和が3の倍数になるのは・・・
と論述を進める人が多いですが、「3個のサイコロを振る$\Rightarrow$目の出方は$6^3$通りある」という流れについて根拠を示す必要があります。
三つのサイコロを区別する.それぞれのサイコロの目の出方は6通りあり,各サイコロの目の出方は独立なので,サイコロの目の出方は$6^3$通りあり、そのうち和が3の倍数になるのは・・・
このように前提から一個一個ゴールにたどり着くために必要な要素を根拠とともに示していき、最終的に完成したものが解答となります。
必要条件にまつわる解答の書き方の例はこちらの問題参照。
ゴールからたどる
解答方針を考えるにあたって、問題のゴールから逆にたどって、「問題のゴールにたどり着くためには何がわかればよいのか?」をまず考えることは有効です。
問題
$0 < x < 1, 0 < y < 1, 0 < z < 1$のとき、次の不等式が成り立つことを証明せよ
\[\begin{aligned} (1) & xy + 1 > x + y\\ (2) & xyz + 2 > x + y + z\\ (3) & xy^2z + 3 > x + 2y + z \end{aligned}\]解答(1)
ゴールを同値変形して解きやすい形に問題を変形します。
$ 0<x<1, 0 <y< 1 $ より $x-1 < 0$, $y-1 < 0$ なので
\[xy + 1 - (x + y) = (x - 1)(y - 1) > 0 \therefore \: \: xy + 1 > x + y\]解答(2)
$0 < xy < 1$なので(1)より
\[xyz + 2 = (xy)z + 1 + 1 > xy + z + 1\](1)より $xy + z + 1 > x + y + z$なので、題意が示された。
解答(3)
$ 0 < xy < 1$, $ 0 < yz < 1$なので(1)より
\[xy^2z + 3 = (xy)(yz) + 1 + 2 > xy + 1 + yz + 1 > x + y + y + z\]よって題意が示された.
■
定義に立ちかえる
糸口がわからないとき、まず考えるべきことは、問題文中の言葉および記号の意味がはっきりわかっているか、ということです。そこをおさえることで解決の糸口がつかめることが少なくないです。それを「定義に立ちかえる」とここでいいます。それには二つの側面があります。
- 学校で習ったはずの言葉の正確な意味を押さえる
- 出題者が定めた記号の意味を, 自分がわかっている言葉で言い換える
補助問題を探す
解きたい問題が難しい場合には、少し易しい問題に変形して解いてみると、基の問題を解くためのヒントを得られる場合があります。この少し易しい問題のことを補助問題といいます。
\[x^4 - 13x^2 + 36 = 0\]例
という方程式を満たす$x$を求めたいとします。$y = x^2$とおくと
\[y^2 - 13 y + 36 = (y-4)(y-9) = 0\]と求めやすい問題に変形することができます。よって、$y \in (4, 9)$ Then, $x \in (-3, -2, 2, 3)$$
■
補助問題の条件
補助問題はあくまでメインの課題を解くために作り出すものです。なので補助問題であるための必要条件として以下が挙げられます:
- 補助問題はメインの問題よりも解きやすいものでなければならない
- 補助問題はメインの問題よりも解きやすいと事前に予測できなければならない
- 補助問題はメインの問題を解くにあたって役に立つもの、踏み石的存在でなければならない
補助問題の見つけ方:同値変形
基本的には直面している問題を同値変形することで補助問題を見つけていきます。
$p$が等式や命題(等式も命題だが)であるとき, $p \iff q$と同値関係を保って別の等式や命題 $q$ に変形することを同値変形といいます。例えば
\[\begin{aligned} x - \sqrt{x - 1} = 3 &\iff x - 3 = \sqrt{x - 1}\\ &\iff (x - 3)^2 = x - 1 \:\text{ かつ }\: x\geq 3\\ &\iff x^2 - 7x + 10 = 0 \:\text{ かつ }\: x\geq 3\\ &\iff (x - 2)(x - 5) = 0 \:\text{ かつ }\: x\geq 3\\ &\iff x = 5 \end{aligned}\]補助問題は同値変形かどうか確認することは重要です。与えられた条件からもっと狭い条件に変形してしまうと解が減ることになるし、広くしてしまうと不適当な、その問題となんの関係もないでたらめな解を持ち込むことになります。
考える方法としての必要条件
基本的には同値変形を繰り返していけばよいですが、それが簡単ではない場合,「必要条件で絞ったものを個別に確認する」という方針は有効です。つまり、
- 問題の条件や仮定を使って、いくつかの候補に絞る
- その候補を1つずつ調べて答えを探す
例題
すべての正の整数 $n$ に対して $5^n+an+b$ が16の倍数となるような16以下の正の整数 $a,\ b$ を求めよ.
\[f(n) = 5^n + an + b\]解
とおきます。すべての正の整数 $n$ に対して$f(n)$は16の倍数なので
\[f(16) = 5^{16} + 16a + b \equiv 1 + b \: \text{ mod } 16\]よって、$b = 15$。
同様に
\[f(1) = 5 + a + 15 = 20 + a\equiv 0 \: \text{ mod } 16\]よって、$a = 12$と必要条件とわかる。
つぎに、$(a, b) = (12, 15)$が十分条件であることを示す。
\[\begin{aligned} f(n) & = 5^n + 12n + 15\\ & = (1 + 4)^n + 12n + 15\\ & = 16 + 16n + (_nC_{n-2}4^2 + \cdots + 4^n) \because \text{ 二項定理} \end{aligned}\]よって、十分条件であることが確認された。
■
発見的推理:具体例を観察して規則性を見つける
抽象的な問題,一般的に自然数 $n$ について証明する問題などでは, 例を作って考えることが問題をとらえるうえで有効です。流れとして以下です:
- こうではないかという仮説を立てる
- それを個別実験で確かめる
- 実験でまちがいないとなると,なぜそれが成り立つのか理論を追求する
ステップ1, 2をクリアした段階で得られた推測を発見的推理といいます。この発見的推理は個別事例では成り立つが、最終的に解きたい問題にはまだ直接適用することはできません。発見的推理は厳密な解答方針の立案には役に立ちますが、あくまで発見的推理は最終的で厳密なものではなく仮のものであり、厳密な解と混同してはなりません。
モーザーの円分割問題:誤った推論
円周上に $n$ 個の頂点を打ち,その全ての2頂点間を線分で結ぶ。このとき,円は $M$ 個の領域に分割されるとする。ただし、円の内側において3本以上の線分が一点に交わることはないようにする。このとき、$M$は$n$によってどのように表されるか?
誤った推論
「具体例を観察して規則性を見つける」という方針で考えてみます。点が一個のときは1個の部分に分割、点が2個のときは2個に分割。これで点5個まで調べていくと以下のような関係性になります。
\(\begin{array}{|c|c|c|c|c|} \hline n\text{点の個数} & 1 & 2 & 3 & 4 & 5 \\ \hline M & 1 & 2 & 4 & 8 & 16 \\ \hline \end{array}\)
別れた部分の個数は点が1個増えるたびに2倍となる関係性があると推測できます。$M = 2^{n-1}$と予測するのは妥当と思われます。しかし、$n = 6$のとき、$M = 31$となってしまい、予測が正しくないことが確認できます。よって、「いくつかの具体例で正しいからすべての場合に正しい」と推論してはならないとわかります。
正しい解答
$k+1$ 個の頂点がある場合について考える。頂点を(時計回りの順番で)$P_0,P_1,\cdots,P_k$とします。$P_1, \cdots ,P_k$ たちを結ぶ線分によって領域は $M_k$ 個に分割されているとします。そこに線分 $P_0P_i:(i=1,\cdots,k)$を追加することで領域がいくつ増えるかを考えます。

既存の弦と交わるたびに領域が1個ずつ増えて, 点 $P_i$ に達したときに領域がさらに1個増えます。線分 $P_0P_i$ は $(i−1)(k−i)$ 本の線分とぶつかるので,領域を $(i−1)(k−i)+1$ 個増やします。よって、$P_0$を追加することで
\[\begin{aligned} M_{k+1} - M_{k} &= \sum_{i=1}^k\{(i−1)(k−i)+1\} \\ &= -\frac{k(k+1)(2k+1)}{6} + (k+1)\frac{k(k+1)}{2} + (1 - k)k\\ &= \frac{1}{6}k^3 - \frac{1}{2}k^2 + \frac{4}{3}k \end{aligned}\]$M_1 = 1$なので, $n \geq 2$について、
\[\begin{aligned} M_n &= M_1+\sum_{k = 1}^{n-1}\frac{1}{6}k(k^2-3k+8) \\ &= 1+\frac{1}{6}\sum_{k = 1}^{n-1}(k^3-3k^2+8k) \\ &= 1+\frac{1}{6}\left\{\frac{1}{4}(n-1)^2n^2\right. \\ &\qquad \left.-3\cdot\frac{1}{6}(n-1)n(2n-1)+8\cdot\frac{1}{2}(n-1)n\right\} \\ &= 1+\frac{1}{24}(n-1)n\{ (n-1)n-2(2n-1)+16\} \\ &= 1+\frac{1}{24}(n-1)n(n^2-5n+18) \\ &= \frac{1}{24}(n^4-6n^3+23n^2-18n+24) \end{aligned}\]が得られる. これは $n=1$ のときも成り立つ. ゆえに, すべての正の整数 $n$ に対して
\[M_n = \frac{1}{24}(n^4-6n^3+23n^2-18n+24)\]が成り立ちます。
■
例:次元によるテスト
次元によるテストは幾何学や物理学の問題を試すのによく知られた方法です。単振動、すなわち小さくて思い物体が一定の長さの重さのない紐の先に吊るしてあるものを考えます。
- $l$: 紐の長さ
- $g$: 重力加速度
- $T$: 振り子の周期
ここで振り子の周期が紐の長さと重力加速度とどのように関係しているか調べたいとします。力学的推論によって、
\[T = cl^mg^n \: \text{ where } m, n \text{ is constant}\]と予測したとします。このとき定数$c, m, n$をどのように定めればいいのかが論点となります。そこで次元に注目します。
$T$は周期だから時間によって表されその単位は $sec$, $l$は長さなので $cm$, $g$は加速度なので $cm/sec^2$. 定数 $c$は $cm^0 = 1$ とします。次元のテストは
\[sec = 1\cdot (cm)^m\cdot (cm/sec^2)^n = (cm)^{m+n} \cdot (sec)^{-2n}\]左辺と右辺の単位は同じでなければならないので
\[m+n = 0, -2n = 1\]よって、
\[n = -\frac{1}{2}, m = \frac{1}{2}\]を得ます。ただし、$c$の値はわかりません。また、この推論が確からしいかどうかはわかりません。
組織化
問題を解くにはばらばらの事実を寄せ集めただけでは不十分です。それらの事実を結びつけて、当面の問題に適した形にまとめ上げることが必要です。このまとめ上げる活動をここで知識の「組織化」と呼びます。解答方針を作成することはまさに知識の「組織化」活動です。地道に課題解決を実践していくことで身につけていくものですが、一旦「組織化」を実施したあとに次のことを自問自答することは有効です
- すべてのデータ/条件をつかったか?
- 問題に含まれている大切な概念はすべて考慮にいれたか?
5. 解答方針に基づき解答実行計画をたてる
実行計画を書くにあたっての基本方針は、
- 「最終的に伝えるべきメッセージ(解答)」を考えたとき、じぶんならどういう分析結果があれば納得するのか?
- その分析結果へ、どのような手順でたどり着くのか?
- 他人が解答の正しさを検討できるようになっているか?
となります。
ゴールまでの過程をもれなく記述する
実行計画を書くときには、自分と他人が正しさを検討できるように書かなくてはなりません。そのためには、原則として、問題のゴールに至る計算や論理展開の道筋をもれなく記述することが良いです。ただし、読み手が簡単に再現できる過程まで詳しく書いてしまうと、伝えたい本丸のメッセージが埋もれてしまうデメリットがあります。
しかし、答えを短くするのは、一旦計画を記述したあとでもできるので、まず初手では全体の工程をもれなく記述することが重要となります。
実行計画を実施前に振り返る
実行計画を書いた後、すぐに着手するのではなく、その確からしさを検討することは有用です。これについて、以下のポイントを自問自答することがおすすめです
- 与えられたデータ/条件をすべて使ったか?
- 問題に含まれる本質的な概念はすべて考慮したか?を考える
- 結果をためすことができるか?
- わかりやすくするため、無駄な議論を省く
議論の無駄を省くことは特に重要で、議論の流れのわかりやすさを向上させるだけでなく、実行計画の省エネルギー化も効果として期待できます。長ったらしい計画は、議論の方向性があっていても実行時にミスを招くリスクがあります。
テストケースの作成
実行計画作成の段階で、実行後に得られる結果のテストケースを用意します。テストケースを明確化することで、
- 最終的に得られる結果が自分たちがもともと意図したものなのか?
- 意図している結果の条件はなんなのか?
- 実行計画作成の段階で、考慮すべき項目をちゃんと考慮しているのか?
を言語で明確化することができます。
進捗管理方法の作成
進捗管理方法を定めることで、実行段階において、誰がどのステータスにいて、いつまでになにをやらなくてはならないか?を明確化することできます。これの効果は
- 問題を解くにあたって迷子になることでモチベーションが下がってしまうことを防止する
- 進捗状況が予定通り行かない場合、もともとの計画が間違っている可能性があり、その兆候を早く見つけることができる
- その兆候を早く見つけることで、もっと良いやり方に切り替えることを考えることができる
- 無駄なことをやらなくても良くなる
ということが挙げられます。
実行に入る前の確認ポイント
- 課題解決策が満たすべき条件の明確化
- その条件が満たされているかのテストケースの策定
- 進捗管理の文脈における各段階のマイルストーンの明確化
- 計画修正手続きの整備
計画修正手続き: Keep-Problem-Try
計画を実行する段階になると、何かしらの問題が発生して計画通りに事が運ばないことが必ず発生します。常に計画修正の機会は訪れます。なので、定期的に振り返りミーティングを実施する体制を事前に作っておくことは重要です。
振り返りミーティングを実施するにあたって、KPTというフレームワークで問題を整理することは有用です。例えば、iPhoneアプリケーションのビルドのため、CI用マシンにMacを使用し、サーバも同じマシンでビルドを実行していたとき、継続的インテグレーションに使用しているマシンのスペックが見積もりが甘く低すぎたため、ビルドに要する時間が長いというProblemが発生したとします。ここでTryとして、サーバのビルドとスマートフォンアプリケーションのビルドを分離するという案が出るという具合です。
分析計画例
因果推論における実行計画
| 構成要素 | 説明 |
|---|---|
Research Question |
the causal relationship of interestはなにか? |
Theory |
参考となる理論モデルはあるか?その理論モデルからどのような仮説が導き出されるか? |
Ideal Experiment |
the causal effect of interestを推定するにあたって理想的な実験はなにか? |
Data Set |
使われているデータセットは何か? the causal relationship of interestを特定するのに役立つ特徴はなにか? Dデータセットには欠点があるか? |
Descriptive Evidence |
対象となる変数の間に関係があることを示唆する記述的証拠(相関関係)は何か? |
Identification Strategy |
An identification strategyとは研究者が観察データ(すなわち、無作為化試験によって生成されていないデータ)を実際の実験に近づけるために使用する方法のことです 説明変数の内因性の問題は、論文の中では議論されているか? regressorsのvariationはどのようにして発生しているのか? 推定式に含まれていない変数の影響はあるか? missing variableによって発生するバイアスの方向性はどのようなものか? 他の潜在的なバイアスの原因は考えられるか? 偏りの原因ごとに、データ生成プロセス、推定式、推定量を書く その推定量が偏っている理由を説明する |
Discussion |
さらにどのようなロバストネスチェックを行うことができるか? |
Conclusion |
なぜあなたの結果は重要なのか?どのようなpolicy implicationが考えられるか? |
事業会社におけるAIシステム導入とPOC
業務にAIシステム導入する際、そのシステムが本当に業務改善、ひいては事業PLの改善につながるかをテストするために、構想 → POC → 業務適用という流れで導入が検討されます.

ただ、「構想」の段階で立ち往生になってしまうプロジェクトも数少なくありません. なぜこのようなことが起こるかはシンプルで、「会社はどのような方向性を目指しているのか」「事業レベルでどのような事が課題なのか」「課題を解決するためにはなにが障壁になっているのか」「技術の力で課題をどのように解決できるのか?」「システムは業務にどのように適用することができるのか?」「効果検証はどのような計画に基づいて実施すべきか?」「開発リソースの確保はどのようなプランに従うのか」という絶対に抑えなくてはならない点を抑えることができてないからです。ではなぜ、抑えることができないかというと (1) 事業課題を理解している人 (2) Technologyを理解している人 (3) Operationを理解している人 (4) プロジェクトをまとめる経験を持っている人 がそのプロジェクトに存在しない、または適切にコミュニケーションできないからです. 事業会社において、(1)と(3)の人材はいると思いますが、(2)と(4)を備えた人は少ない/存在しない場合が多いです. その人材ギャップを埋めるために外部のデータ分析会社を雇い、サポートメンバーとして入ってもらうという形でプロジェクトを進行する場合が多いです.
また、進行方向についても一つの工夫があります. 上で紹介した「構想 → POC → 業務適用」という一方向的な流れを
1
構想 → POC → 構想 → POC → ・・・ → 業務適用
という形でプロジェクトを回すパターンもあります. POCを行うと、Biz側もシステムに対する理解が深まり、業務フローに関する意見やシステムが課題解決につながるためにどのような変更をしたほうがいいのか?というFBを得ることが多いです. ですので、これら有益なFBをシステムに反映するために、はじめのPOCを「業務的な合理性検証」に絞り、短いサイクルで実施し、構想の修正/方針変更を途中で考えることができるフェーズを用意します。その後、モデル精度/効果検証にフォーカスしたPOCを行うことで、より課題解決と業務適用に適したシステムを構築することができるようになります.
6. 計画を実行する
計画を実行することは、解答計画を立案するに比べて易しいです。必要なのは「当たり前のことを当たり前にやっていく」精神くらいです。これはただ闇雲に計画を実施していくことではないことに注意してください。あくまで課題解決を目的にその実行計画を実施していくという文脈を忘れないようにしましょう。
当たり前のことを当たり前にやっていくためには
- 解答方針と解答計画の全体像を理解する
- 忍耐力をもって計画を実行する。
- 失敗してもなぜ失敗したか検証する
- 闇雲に計画を実行するのではなく、形式的論理的に実行計画に矛盾がないか常に確認する
- 解答計画はあくまで大枠。実際の実行によって生まれる成果物たちが、その計画の枠内に収まっているか常に確認する
- 実行計画が複雑な場合は、その計画を大きな段階にわけ、それぞれの段階が矛盾がないか確認する。その後、大きな各段階を更に細かい段階に分け、そこでも矛盾がないか検証する。
実行スピードと計画修正
計画が完璧でも実行スピードが遅ければ仕事の価値はどんどん失われていきます。よく多く見られる症状として、丁寧にやりすぎる、または詳細にこだわるあまり、最終的なアウトプットを出す時間が必要以上にかかってしまうケースがあります。この症状を回避するための指針は以下です:
- 「受け手にとっての十分なレベル」を明確化し、やりすぎないように意識する
- 即断即決の弊害として考えられる誤った方針に基づく計画実行は、計画修正によって対応する
- 多くのやり方を準備しておき、一つの方法がうまく行かなければ。別の手法に切り替える
結局の所、計画立案段階で(1) 課題解決策が満たすべき条件の明確化、(2) その条件が満たされているかのテストケースの策定、(3) 進捗管理の文脈における各段階のマイルストーンの明確化、(4) 計画修正手続きの整備ができているかに依存します。
7. 振り返る
問題を理解し、計画を立て、各段階を検討した上で、計画を実行したとする。しかし、どんなに慎重にそれぞれのステップをこなしたとしても間違いを完全に防ぐことはできません。そのため、どんなときにも計画を実行して得られた結果を検証・振り返ることは必要です。振り返りというプロセスで重要な指針は以下となります:
- 結果や議論を手っ取り早く素早く直感的に試すことができるか?
- 直感的に理解できるか?
- 同じ結果を違った仕方で導くことはできるか?
- 他の事柄との関連で理解できるか?
- 得られた結果を別の事柄に応用できるか?
結果を利用できないか?
一般化/特殊化/類推/分解と結合を通じて、得られた解決策が他の問題に応用することができるか?と考えることは有用です。一つの問題を解くことで、今まで解けなかった別の問題も解けるようになるケースがあるからです。課題解決をスケールすることは、効率の良い働き方を実現することに繋がります。
また、課題解決方法を抽象化して全員が実践できるレベルで共有し、再現性をもたせる仕組みも整備することも重要です。組織が大きくなるにつれて、個人個人の質の高さをキープするのは難しくなります。課題解決方法のパーツを組織として用意することで、仮に個人レベルでは二流が大半であっても、組織全体として一流に近い仕事ができる集団になれます。
結果を試すことはできるか?Robustness test
課題解決の流れにおいて、手法上の制約などの理由によりなんらかの仮定は必ず存在します。その仮定が正しいかどうかを心配して、
- その仮定が正しいかどうか
- その仮定が正しくなかった場合に我々の結果が変わるかどうか
をチェックし、得られた結果が偶然の産物じゃないかを確認する必要があります。一般的にはRobustness checkといいます。気をつけるべき点は、あくまで分析の本質的な仮定に関してのみ Robustness checkを実施すべきです。すべての仮定に関してテストできるならばいいですが、時間的制約ないしメッセージの理解しやすさの観点から、本質的仮定のみRobustness check実施すれば十分です。
次にどのように活かしていくか?
もしかしたら課題解決が失敗に終わる場合もありえます。失敗しても、必ず前に戻って、自分達の考え方とか、やり方のどこが間違っていたのか振り返って、次に活かす。そして、再び挑戦する、次の大成功につなげていきます。この環境を作ることも課題解決をデザインすることの重要なポイントとなります。
8. 問題解決の例
ビジネスにおける本質的な選択肢の例
「ある商品Aが売れない」という理由を検討しているします。まだ仮説が出ていないのでまず仮説を設定します。
- 商品Aに商品力がない
- 商品Aに商品力はあるが、マーチャンダイジングに失敗している
- 商品Aに商品力はあるが、マーケティングに失敗している
が考えられます。
全体の売上が下がっているという問題に直面している場合
- 会員数が下がっている
- 会員一人あたりの一回の平均購買金額が下がっている
- 会員一人あたりの期間あたりの購入回数が減っている
が考えられます。どの仮説が正しいかに応じてアクションが異なるため、本質的な選択肢といえます。
課題ベースでストーリーを組み立てる
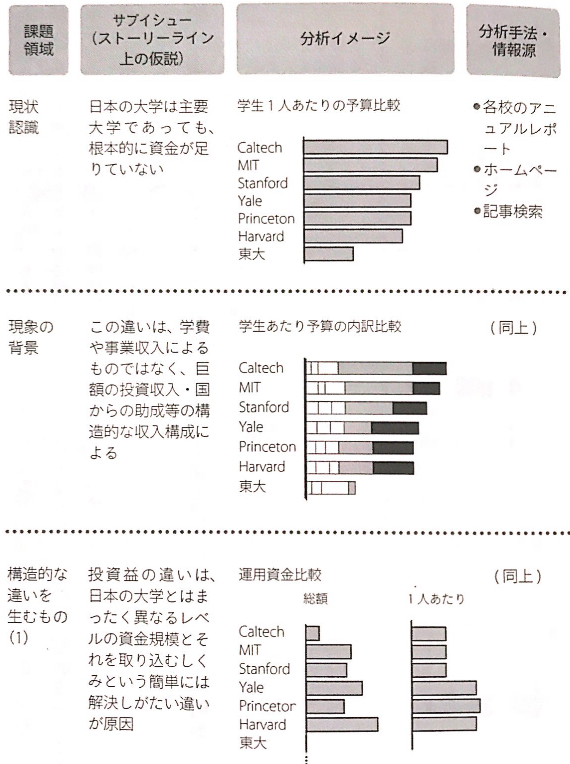
「現在、国内大学が行っている統廃合やコスト削減は財源問題の解決策となるか?」という課題について考えたいと思います。この課題を考えるにあたってのストーリーの一例は以下のようになります:
| 役割 | 内容 |
|---|---|
| 現状及び課題認識 | 日本の大学の財源問題は存在するか? |
| 課題発生のメカニズム | 日本の大学の収入構造はどのようになっているのか? |
| ゴールの設定 | 目指すべき財政運営はどのようなものがあるのか?海外大学のモデルの紹介 |
| 現状とゴールのギャップの評価 | 目指すべき財政運営を導入するにあたってどのような問題があるか? |
| 提案されている策の評価 | 現在提案されている政策が上で挙げた問題を解決することができるか評価する |
| 結論,提案 | 列挙した問題の解決、及び根本的な課題解決するためにはどのような政策が考えられるか? |
速度の問題
問題文
水が直角円錐形の容器に速度$r$で注がれている。容器の底は水平であり、頂点が下を向いているとする。底の半径を$a$, 円錐の高さを$b$とする。水の深さが$\gamma$であるときに水面が上昇する速さを求めよ。
解答方針
| 検討項目 | 説明 | |
|---|---|---|
| (1) | 求めるものは何か? | 水面が上昇する速さ。速さとは水の深さが上昇する速度のこと。つまり$\gamma$の変化の速度のこと |
| (2) | 変化の速度とは何か? | 時間を$t$とおいたとき、$d\gamma/dt$と表される。 |
| (3) | 与えられたデータうち速度を表すものはあるか? | $r$は水の体積の変化の速度を表しています。 |
| (4) | $r$は水の体積の変化の速度を表しているとは? | 容器の体積を$V$とするならば、$dV/dt = r$ |
以上のことを踏まえると、まず水の高さ$\gamma$のときの体積の変化率は以下のように表せます:
\[\frac{dV(\gamma)}{dt} = \frac{dV(\gamma)}{d\gamma}\frac{\gamma(t)}{dt} = \frac{\pi a^2\gamma^2}{b^2}\frac{\gamma(t)}{dt} = r\]よって、
\[\frac{\gamma(t)}{dt} = \frac{rb^2}{\pi a^2\gamma^2}\]この結果は、高さが高いほど変化の速度が小さくなっていることを示しており、直感的にも理解することができます。
■
必要十分条件の見極め
問題文
$a$は実数の定数とする.
$$ a_1 = a, a_n = 3^n - 5a_{n-1} (n\geq 2) $
で定まる数列${a_n}$について,次の問いに答えよ.
- 一般項$a_n$を$a$と$n$の式で表せ.
- 任意の自然数$n$に対し,$a_{n+1}>a_n$が成り立つときの$a$の値を求めよ.
解答(1)
与えられた式を次のように変換します:
\[\begin{aligned} a_n &= 3^n - 5a_{n-1}\\ &= 3^n + -5\cdot a_{n-1} \end{aligned}\]両辺に$(-5)^n$を掛けて
\[\frac{a_n}{(-5)^n} = \left(-\frac{3}{5}\right)^n + \frac{a_{n-1}}{(-5)^{n-1}}\]ここで、
$b_n\equiv \frac{a_n}{(-5)^n}$$
と定義します。
\[\begin{aligned} b_n &= b_1 + \sum_{i=2}^n\left(-\frac{3}{5}\right)^i\\ &= b_1 + \left(\frac{3}{5}\right)^2 \sum_{i=0}^{n-2}\left(-\frac{3}{5}\right)^i\\ &= b_1 + \frac{9}{25}\frac{1 - \left(- \frac{3}{5}\right)^{n-1}}{1 + \frac{3}{5}}\\ & = b_1 + \frac{9}{40}\left\{1 - \left(- \frac{3}{5}\right)^{n-1} \right\} \end{aligned}\] \[\therefore a_n = (-5)^{n-1}\left(a - \frac{9}{8}\right) + \frac{3^{n+1}}{8}\]■
解答(2)
解答(1)より
\[\begin{aligned} a_{n+1} - a_n &= (-5)\left(a - \frac{9}{8}\right)(-5)^{n-1} + \frac{3^{n+2}}{8} + \left(a - \frac{9}{8}\right)(-5)^{n-1} - \frac{3^{n+1}}{8}\\ &= \frac{3^{n+1}}{4} -6\left(a - \frac{9}{8}\right)(-5)^{n-1} \end{aligned}\]これより、
\[a - \frac{9}{8} = 0\]ならば、すべての自然数$n$で$a_{n+1} - a_n > 0$が成立する。よって、$a = \frac{9}{8}$は十分条件である。
次に、$a = \frac{9}{8}$が必要条件でもあることを示す。
\[\frac{3^{n+1}}{4} -6\left(a - \frac{9}{8}\right)(-5)^{n-1}\]を$n = 2k, 2k+1$に応じて、$(-5)^{n}$で割ると
\[\begin{aligned} &-\frac{5}{8}\left(\frac{3}{5}\right)^{2k} < a - \frac{9}{8}\\ &\frac{5}{8}\left(\frac{3}{5}\right)^{2k+1} > a - \frac{9}{8}\\ &\Rightarrow -\frac{5}{8}\left(\frac{3}{5}\right)^{2k} < a - \frac{9}{8} < \frac{5}{8}\left(\frac{3}{5}\right)^{2k+1} \end{aligned}\]を得ます。これがすべての自然数$k$で成立するので
\[\left|a - \frac{9}{8}\right| < \frac{5}{8}\left(\frac{3}{5}\right)^{2k}\]$k$を十分大きくすると、右辺はいくらでも小さくなるので
\[\left|a - \frac{9}{8}\right| = 0\]よって、$a = \frac{9}{8}$は必要条件でもあります。
■
等しいものを文字に置く
二つ以上の等号でむすばれた条件などは, その等しいものを別の文字で表すことによって, 論証が簡明になることが多いです。
問題
相異なる3数 $a, b, c$ が
\[\frac{a^3+2a}{a+1} = \frac{b^3+2b}{b+1} = \frac{c^3+2c}{c+1}\]を満たすとき,$a + b + c$ 及び $abc + ab + bc + ca$の値を求めよ.
\[\frac{a^3+2a}{a+1} = \frac{b^3+2b}{b+1} = \frac{c^3+2c}{c+1} = k\]解答
と置きます。すると、
\[\begin{cases} a^3 + 2a &= k(a+1)\\ b^3 + 2b &= k(b+1)\\ c^3 + 2c &= k(c+1) \end{cases}\]よって三変数a, b, cは3次方程式
\[x^3 + (2 - k)x - k = 0\]の3解とわかります。 3次方程式の解と係数の関係から、
\[\begin{aligned} & a + b + c = 0\\ & ab + bc + ca = 2 - k\\ & abc = k \end{aligned}\] \[\therefore a + b + c = 0 \:\text{ and }\: abc + ab + bc + ca\]■
どの化粧品を買っていいかわからない
「どの化粧品が良いのかわからない」という悩みを持っている人は多いと思います。「どの化粧品が良いのかわからない」という課題に直面しているのは理解できますが、これは本質的なものではありません。化粧品は美しくなるために使用するもので、化粧品を用いて解決したい課題はなにかをまず考える必要があります。考える順番としては、
- 今悩んでいる症状はなにか?
- その症状はなぜ発生するのか
- 課題解決方針はなにか?
- 課題解決方針に適した化粧品はなにか?
この順番はイプサでカウンセリングを受けたときも同様の流れでした。今回は仮にシミを解消したい場合を考えます。
シミのメカニズム
シミは肌に黒メラニンが過剰に蓄積し、肌が部分的に茶色に見える状態です。メラニンの発生と蓄積の2つを理解する必要があります。
(1) メラニンの発生と紫外線
メラノサイトという細胞がメラニンを生成します。なぜメラニンを作るかというと、紫外線が原因となって肌が傷つけられたとき肌を守るためメラニンという色素が作られます。このメラニンは日傘の役割をします。この日傘を角化細胞(ケラチノサイト)に渡して紫外線から肌を守っています。
(2) メラニンの過剰蓄積
シミはメラニンが肌に過剰に蓄積されることで発生する症状です。過剰に蓄積される原因として、(1) メラニンが過剰に生産され過剰にケラチノサイトに渡される、(2) メラニンの排出が滞るの2つが考えられます。(1)の過剰に生産されることに関しても、肌センサーがバグって生成の必要がないタイミングでメラノサイトにメラニン生成信号を渡す場合やメラノサイトが過剰にセンサーに反応してしまうという2つのケースが考えられます。
課題解決方針と美容成分
以上のシミ発生メカニズムを踏まえるとシミの解決方針は以下となります:
| 方針 | 具体アクション |
|---|---|
| 紫外線から肌を守る | 日焼け止め |
| 間違ったメラニン生成命令をストップする | カモミラET トラネキサム算 トラネキサム算セチル塩酸塩 |
| 過剰なメラニンの産生を抑制する | ビタミンC誘導体 コウジ酸 アルプチン エラグ酸 4-n-ブチルレゾルシン リノール酸S 4-メトキシサリチル酸カリウム塩など |
| メラニンの受け渡しをブロックする | ニコチン酸アミド |
| 滞ったメラニン排出促進 | アデノシン一リン酸二ナトリウムOT デクスパンテノールW |
これでカタログに記載されてある成分がお肌環境をどう変えるかを理解することがちょっとできるようになります = 自分が欲しい商品が見つかる。
Appendix
関係者を説得する: メッセージドリブン
ビジネスにおける問題解決の最終的なアウトプットは、具体的アクションを関係者を巻き込んでリード/実行し、本丸の事業課題を解決することです。この文脈において、自分が提案する解決策を関係者に周知する工程を経る必要があります。このとき意識すべきポイントとして、
- 意味のある課題を扱っていることを理解してもらう
- 最終的な解決策を理解してもらう
- 解決策に納得して、一緒に行動してもらう
- タイムリーにこれらを実現していく
どのように伝えるべきか
基本的には自分が課題設定で定めたストーリーラインに従って、伝えるべきメッセージを選定します。このとき、
- 論理構造は整理されているか?
- 流れが悪いところはないか?前提条件は欠けてないか?
- 結論を端的に説明できるか?
- エレベーターテストに耐えられるか?
一例として、「今はこういう状況である」「なにもしないとこうなる」「われわれはこういう未来を描いている」「描いた未来を実現するために、今これをやる必要がある」という項目を完結に話せるかどうか、自問してみてください。
Tips
- 「や」ができきたらもうちょっと短くできるか疑え
- 受け手にとって曖昧になるような言葉は使わない
- 結論とプログレスをわけろ
Rerefences
- いかにして問題を解くか ISBN13:978-4-621-04593-0
- イシューからはじめよ ISBN13:978-4-86276-085-2
- 問題を解く
- How-to-Write-a-Research-Paper-in-Economics
- Some tips for robustness checks and empirical analysis in general
- Robustness Tests: What, Why, and How
-
有名問題・定理から学ぶ数学
(注意:GitHub Accountが必要となります)