ユークリッドの互除法とジェネラティブアート

	概要
目的	Processingでユークリッドの互除法の可視化
参考	- ユークリッドの互除法の証明と不定方程式 - 一次不定方程式ax+by=cの整数解 - 数学から創るジェネラティブアート―Processingで学ぶかたちのデザイン

1. ユークリッド互除法とは？
2. 拡張ユークリッド互除法
- 不定方程式の定理
  - 証明
- ユークリッド互除法の一次不定方程式への応用
3. Processingを用いたユークリッド互除法の可視化
4. 再帰的分割
Appendix: Processingによる色の指定
- HSB色空間
- Processing における色の指定

1. ユークリッド互除法とは？

ユークリッド互除法は与えられた２つの自然数に対し、その最大公約数を求めるアルゴリズムです。

ユークリッド互除法

2つの自然数 $x_0, x_1$ に対して、最大公約数は次の手順により求めることができる。

1: $x_0$ を $x_1$ で割り、その余りを $x_2$とする
2: $x_1$ を $x_2$ で割り、その余りを $x_3$とする
3: $x_2$ を $x_3$ で割り、その余りを $x_4$とする
この操作を割り切れるまで繰り替えす
n: $x_{n-1}$ を $x_n$ で割りきれた。このとき、$x_n$が最大公約数である。

ユークリッド互除法の実装

def gcd(a, b):
    """Calculate the greatest common divisor of a and b"""
    if not (isinstance(a, int) & isinstance(b, int)):
        print("At least one of the inputs is not integer")
        return None

    while b > 0:
        a, b = b, a % b
    return a

ユークリッドの互除法の証明

a を b で割った商を q，余りを r とおくと，

\[a = bq + r\]

このとき、

\[gcd(b, r) \geq gcd(a, b) \text{ and } gcd(a, b) \geq gcd(b, r)\]

が証明できれば、

\[gcd(a, b) = gcd(b, r)\]

となります。

(1) $gcd(b, r) \geq gcd(a, b)$ について、

$a$ と $b$ は $gcd(a,b)$ の倍数なので，

\[r=bq−a\]

も $gcd(a,b)$ の倍数になる。よって，$gcd(a,b)$ は $b$ と $r$ の公約数。最大公約数は公約数の中で最大のものなので，

\[gcd(b, r) \geq gcd(a, b)\]

(2) $gcd(a, b) \geq gcd(b, r)$について、

$b$ と $r$ は $gcd(b,r)$ の倍数なので，

\[a=bq+r\]

も $gcd(b,r)$ の倍数になる。よって，$gcd(b,r)$ は $a$ と $b$ の公約数。最大公約数は公約数の中で最大のものなので，

\[gcd(a, b) \geq gcd(b, r)\]

割り算を繰り返し行うと，余りの定義より $b>r$ なので数字はどんどん小さくなっていきます。そして，最後は必ず余りが 0 になって停止します。そのときの割った数が，求めたい最大公約数になっています。

2. 拡張ユークリッド互除法

不定方程式とは，

\[3x+5y=23\]

のように，方程式の数よりも未知変数の数が多いような方程式のことです。拡張ユークリッド互除法は二元一次不定方程式の整数解を求めるアルゴリズムです。

不定方程式の定理

$x, y$ に関する二元一次不定方程式 $ax+by=c$が整数解を持つ $\iff$c は $gcd(a,b)$ の倍数

証明

(1) ⇒を証明します。

$a, b$ は $gcd(a,b)$ の倍数なので, 整数解 $m, n$にたいして $c$も$gcd(a, b)$の倍数。

(2) ⇐ を証明します。

\[a=p\cdot gcd(a,b) , b=q\cdot gcd(a,b)\]

とおきます（ただし、$p, q$は互いに素）。

$p$ と $q$ が互いに素なとき $p,2p,3p, \cdots ,(q−1)p$を $q$ で割った余りは全て異なるので，余りが1となるようなものが存在する。それを$\alpha p$とおき、$q$で割ったときの商を$\beta$とおくと、

\[\alpha p = q\beta + 1\]

よって、$p\cdot m + q\cdot n =1$ は整数解を持つので両辺を$gcd(a,b)$ 倍して，

\[am+bn=gcd(a,b)\]

も整数解を持つことがわかる。

ユークリッド互除法の一次不定方程式への応用

\[8x+11y=1\]

を満たす整数 $(x,y)$を求めたいとします。

まず、$(11, 8)$にユークリッド互除法を適用します。

\[\begin{aligned} 11&=8 \cdot 1+3\\ 8&=3\cdot 2+2\\ 3& =2\cdot 1+1 \end{aligned}\]

これをさかのぼっていく（余りの部分を順々に代入していく）。

\[\begin{aligned} 1&=3−2\cdot 1\\ &=3−(8−3\cdot 2)\cdot 1\\ &=3\cdot 3+8\cdot (−1)\\ &=(11−8\cdot 1)\cdot 3−8\\ &=8\cdot (−4)+11\cdot 3 \end{aligned}\]

つまり，$(−4,3)$が解の1つ。

次に一般解を求めます。

\[8x+11y=8\cdot(-4)+11\cdot 3=1\]

より

\[8(x+4) + 11(y-3) = 0\]

が成り立ちます。このとき、(8, 11)は互いに素なので、

\[\begin{aligned} x + 4 & = 11m\\ y - 3 & = -8m \end{aligned}\]

が成り立ちます。よって、

\[(x, y) = (11m - 4, 3 - 8m)\]

3. Processingを用いたユークリッド互除法の可視化

ユークリッド互除法の図形的意味をまず考えます。以下の条件の長方形を考えます

横と縦の長さがそれぞれ $a, b$
$a, b$はそれぞれ自然数

$a \div b = c \cdots d$の図形的意味は「この長方形から一辺の長さ$b$の正方形を$c$個、余りとして辺の長さ$b, d$の長方形ができる」となります。

ユークリッド互除法を用いた長方形の分割

// 横:縦の比率 = num_A: num_B
int num_A = 10;
int num_B = 6;
int scalar = 40; //長方形の拡大倍率

num_A *= scalar;
num_B *= scalar;

// Parameters
int wd = num_B; 
int x_pos = 0;
int y_pos = 0;
int itr = 0;

//描画
size(410, 250); //windowサイズ

//ユークリッド互除法と長方形の分割
while (wd > 0){
    itr++;
    if (itr %2 == 1){
        while (x_pos + wd <= num_A){ //奇数回目はx軸方向に正方形を増やす
            rect(x_pos+5, y_pos+5, wd, wd); //作画位置の調整 
            x_pos += wd;
        }
        wd = num_A - x_pos;
    }
    else {
        while (y_pos + wd <= num_B){ //偶数回目はy軸方向に正方形を増やす
            rect(x_pos+5, y_pos+5, wd, wd);
            y_pos += wd;
        }
        wd = num_B - y_pos;
    }
};

save("Euclidean_rectangular.png");

このコードを実行すると以下の結果が得られます。

色をつける場合

colorMode()で色を表示するための形式を指定します。RGB形式が一般的ですが、色明るさ彩度を保ったまま色を変えるにはHSB形式が扱いやすいので今回はHSB形式でいきます。

H: 色相
S: 彩度
B: 明るさ

// 横:縦の比率 = num_A: num_B
int num_A = 10;
int num_B = 6;
int scalar = 40; //長方形の拡大倍率

num_A *= scalar;
num_B *= scalar;

// Parameters
int wd = num_B; 
int x_pos = 0;
int y_pos = 0;
int itr = 0;

//描画
size(410, 250); //windowサイズ
colorMode(HSB, 1);

//ユークリッド互除法と長方形の分割
while (wd > 0){
    itr++;
    if (itr %2 == 1){
        while (x_pos + wd <= num_A){ //奇数回目はx軸方向に正方形を増やす
            fill(color(random(1), 1, 1));
            rect(x_pos+5, y_pos+5, wd, wd); //作画位置の調整 
            x_pos += wd;
        }
        wd = num_A - x_pos;
    }
    else {
        while (y_pos + wd <= num_B){ //偶数回目はy軸方向に正方形を増やす
            fill(color(random(1), 1, 1));
            rect(x_pos+5, y_pos+5, wd, wd);
            y_pos += wd;
        }
        wd = num_B - y_pos;
    }
};

save("Euclidean_rectangular_with_color.png");

このコードを実行すると以下の結果が得られます。

長方形による正方形の分割

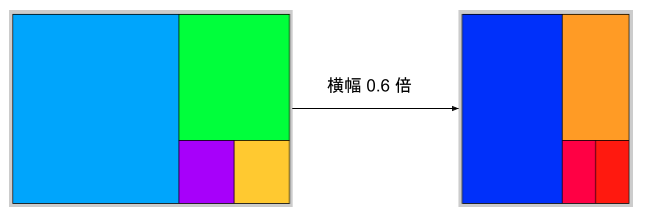
つぎに正方形を横縦比 $b:a$となる長方形で分割したいとする。下の例だと、横縦比$10:6$の長方形を正方形に分割したあとに、横幅を0.6倍すると横縦比$6:10$の長方形で正方形を分割することができます。

正方形を横縦比 $b:a$となる長方形で分割したいので、

\[\text{横}:\text{縦} = b : a = r : 1 = 1 : \frac{1}{r}\]

この比率を活用して、x軸で進む場合は$r$を掛けたwidthで長方形を増やしていき、y軸で進む場合は$1/r$を掛けたwidthで増やしていけば良いことがわかる。これを実装すると、

// オリジナル長方形の横:縦の比率 = num_A: num_B
// 想定している正方形の辺の長さ = num_B
int num_A = 12;
int num_B = 17;
float ratio = (float) num_B/num_A;
int scalar = 40; //長方形の拡大倍率

num_B *= scalar;
num_A *= scalar;
float num_C = min((float)num_A, (float)num_B);


// Parameters
float wd = num_C;
float x_pos = 0; //変更点
float y_pos = 0; //変更点
int itr = 0;

//描画
size(490, 490); //windowサイズ
colorMode(HSB, 1);

//ユークリッド互除法と長方形の分割
while (wd > 0.01){
    itr++;
    if (itr %2 == 1){
        while ((x_pos + wd*ratio <= num_C)){ //奇数回目はx軸方向に正方形を増やす
            fill(color(random(1), 1, 1));
            rect(x_pos+5, y_pos+5, wd*ratio, wd); //作画位置の調整 
            x_pos += wd*ratio;
        }
        wd = num_C - x_pos;
    }
    else {
        while ((y_pos + wd/ratio <= num_C)){ //偶数回目はy軸方向に正方形を増やす
            fill(color(random(1), 1, 1));
            rect(x_pos+5, y_pos+5, wd, wd/ratio);
            y_pos += wd/ratio;
        }
        wd = num_C - y_pos;
    }
};

save("Euclidean_square_with_color.png");

実行結果は以下、

長方形による長方形の分割

長方形による正方形の分割を応用します。

// オリジナル長方形の横:縦の比率 = num_A: num_B

float num_A = 10;
float num_B = 6;
float ratio = (float) num_B/num_A;
int scalar = 40; //長方形の拡大倍率

num_B *= scalar;
num_A *= scalar;
float num_C = min(num_A, num_B);


// Parameters
float wd = num_C;
float x_pos = 0; //変更点
float y_pos = 0; //変更点
int itr = 0;

//描画
size(410, 250); //windowサイズ
colorMode(HSB, 1);

//ユークリッド互除法と長方形の分割
while (wd > 0.01){
    itr++;
    if (itr %2 == 1){
        while ((x_pos + wd*ratio <= num_A)){ //奇数回目はx軸方向に正方形を増やす
            fill(color(random(1), 1, 1));
            rect(x_pos+5, y_pos+5, wd*ratio, wd); //作画位置の調整 
            x_pos += wd*ratio;
        }
        wd = num_A - x_pos;
    }
    else {
        while ((y_pos + wd/ratio <= num_B)){ //偶数回目はy軸方向に正方形を増やす
            fill(color(random(1), 1, 1));
            rect(x_pos+5, y_pos+5, wd, wd/ratio);
            y_pos += wd/ratio;
        }
        wd = num_B - y_pos;
    }
};

save("Euclidean_rectangular_div_rect_with_color.png");

実行結果は以下、

4. 再帰的分割

ここでは長方形を長方形で分割することを考えます。上で考えた長方形による長方形の分割と異なる点は、

長方形を正方形で分割する
分割した結果生まれた正方形を再度長方形で分割する
工程1, 工程2を指定した回数繰り返す

という分割を考えます。

長方形を正方形に分割して再度長方形に分割する

// オリジナル長方形の横:縦の比率 = num_A: num_B

float num_A = 10;
float num_B = 6;
float ratio = (float) num_B/num_A;
float scalar = 40; //長方形の拡大倍率


// Parameters
float wd = num_B*scalar;
float x_pos = 0;
float y_pos = 0;
int itr = 0;

void setup(){//いわゆるmain関数
    num_B *= scalar;
    num_A *= scalar;
    //描画
    size(410, 250); //windowサイズ
    colorMode(HSB, 1);
    
    while (wd > 0){
        itr++;
        if (itr %2 == 1){
            while (x_pos + wd <= num_A){ //奇数回目はx軸方向に正方形を増やす
                rect(x_pos + 5.0, y_pos + 5.0, wd, wd); //作画位置の調整
                div_square(x_pos + 5.0, y_pos + 5.0, wd); //正方形の分割
                x_pos += wd;
            }
            wd = num_A - x_pos;
        }
        else {
            while (y_pos + wd <= num_B){ //偶数回目はy軸方向に正方形を増やす
                rect(x_pos + 5.0, y_pos + 5.0, wd, wd);
                div_square(x_pos + 5.0, y_pos + 5.0, wd); //正方形の分割
                y_pos += wd;
            }
            wd = num_B - y_pos;
        }
    }
}

void div_square(float x_pos, float y_pos, float wd){
    int itr = 0;
    float x_pos_sq = 0;
    float y_pos_sq = 0;
    float num_A = wd;
    float num_B = wd;
    float wd_sq = wd;

    //正方形の分割
    while (wd_sq > 0.001){
        itr++;
        if (itr %2 == 1){
            while ((x_pos_sq + wd_sq*ratio <= num_A)){ //奇数回目はx軸方向に正方形を増やす
                fill(color(random(1), 1, 1));
                rect(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq*ratio, wd_sq); //作画位置の調整 
                x_pos_sq += wd_sq*ratio;
            }
            wd_sq = num_A - x_pos_sq;
        }
        else {
            while ((y_pos_sq + wd_sq/ratio <= num_B)){ //偶数回目はy軸方向に正方形を増やす
                fill(color(random(1), 1, 1));
                rect(x_pos_sq + x_pos, y_pos_sq + y_pos, wd_sq, wd_sq/ratio);
                y_pos_sq += wd_sq/ratio;
            }
            wd_sq = num_B - y_pos_sq;
        }
    }
}

実行結果は以下、

正方形の再帰的分割

正方形を長方形に分割し、それを再度正方形に分割し、分割後の辺の長さが基準値以上に限って再帰的に分割を続けるプログラムを書きます。

// オリジナル長方形の横:縦の比率 = num_A: num_B

float num_A = 10;
float num_B = 6;
float ratio = (float) num_B/num_A;


// Parameters
float x_pos = 0;
float y_pos = 0;
int itr = 0;
float thr = 10;

void setup(){//いわゆるmain関数
    //描画
    size(410, 410); //windowサイズ
    colorMode(HSB, 1);
    float wd = width - 10;

    divSquare(x_pos, y_pos, wd); //正方形の分割
    
    save("Euclidean_recursive_rectangular_2_with_color.png");
}

void divSquare(float x_pos, float y_pos, float wd){ //正方形の分割    
    float x_end_pos = x_pos + wd;
    float y_end_pos = y_pos + wd;
    while (wd > thr){
        itr++;
        if (itr %2 == 1){
            while (x_pos + wd*ratio <= x_end_pos){ //奇数回目はx軸方向に正方形を増やす
                fill(color(random(1), 1, 1));
                rect(x_pos + 5.0, y_pos + 5.0, wd*ratio, wd); //作画位置の調整
                div_rect(x_pos, y_pos, wd*ratio, wd); //正方形の分割
                x_pos += wd*ratio;
            }
            wd = x_end_pos - x_pos;
        }
        else {
            while (y_pos + wd/ratio <= y_end_pos){ //偶数回目はy軸方向に正方形を増やす
                fill(color(random(1), 1, 1));
                rect(x_pos + 5.0, y_pos + 5.0, wd, wd/ratio);
                div_rect(x_pos, y_pos, wd, wd/ratio); //正方形の分割
                y_pos += wd/ratio;
            }
            wd = y_end_pos - y_pos;
        }
    }
}


void div_rect(float x_pos, float y_pos, float x_wd, float y_wd){
    int itr = 0;
    float x_pos_sq = 0;
    float y_pos_sq = 0;
    float x_end = x_wd;
    float y_end = y_wd;
    float wd_sq = y_wd;

    //正方形の分割
    while (wd_sq > thr){
        itr++;
        if (itr %2 == 1){
            while ((x_pos_sq + wd_sq <= x_end)){ //奇数回目はx軸方向に正方形を増やす
                rect(x_pos_sq+ x_pos+5.0, y_pos_sq + y_pos+5.0, wd_sq, wd_sq); //作画位置の調整
                divSquare(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq);
                x_pos_sq += wd_sq;
            }
            wd_sq = x_end - x_pos_sq;
        }
        else {
            while ((y_pos_sq + wd_sq <= y_end)){ //偶数回目はy軸方向に正方形を増やす
                rect(x_pos_sq + x_pos + 5.0, y_pos_sq + y_pos + 5.0, wd_sq, wd_sq);
                divSquare(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq);
                y_pos_sq += wd_sq;
            }
            wd_sq = y_end - y_pos_sq;
        }
    }
}

実行結果は以下、

GUIでパラメーター調整

以下のプログラムを動かすためには、controlP5ライブラリを読み込む必要があります。

// オリジナル長方形の横:縦の比率 = num_A: num_B

import controlP5.*;  //ControlP5ライブラリを読み込み
import processing.pdf.*;  //ControlP5クラスの変数を宣言
ControlP5 cp5;

float num_x, num_y;
boolean rec = false;  //画像保存のための論理型変数
int count;  //描画した長方形の個数を記録する変数
float ratio, thr;

// Parameters
float x_pos = 0;
float y_pos = 0;
int itr = 0;


void setup(){//いわゆるmain関数
    //描画
    size(410, 410); //windowサイズ
    colorMode(HSB, 1);
    
    controller();  //cp5のコントローラを呼び出し
}

void draw(){
  background(1, 0, 1);
  //frameRate(10);
  
  ratio = (float) num_y / num_x;
  count = 0;

  float wd = width - 10;
  if(ratio != 1){  //numAとnumBが異なるとき実行
    randomSeed(0);
    divSquare(x_pos, y_pos, wd); //正方形の分割
  }
  if(rec){
    String namePNG = "gui_recursive_rectangular_" + str(num_x) + "_" + str(num_y) + "_" + str(int(thr)) + ".png";  //PNGの保存ファイル名
    save(namePNG);
    rec = false;
  }
}

//グローバル変数をコントローラで操作する
void controller(){
  cp5 = new ControlP5(this);  //コントローラを生成
  cp5.addSlider("num_x")  //numAの値を動かすスライダー
    .setPosition(10,10)  //スライダーの位置
    .setSize(100,20)  //スライダーのサイズ
    .setRange(1,40)  //最小値と最大値
    .setValue(10)  //初期値
    .setColorCaptionLabel(0)  //スライダーの文字の色
    ;
  cp5.addSlider("num_y")
    .setPosition(10,50)
    .setSize(100,20)
    .setRange(1,40)
    .setValue(6)
    .setColorCaptionLabel(0)
    ;
  cp5.addSlider("thr")
    .setPosition(10,90)
    .setSize(100,20)
    .setRange(1,100)
    .setNumberOfTickMarks(30)
    .setValue(100)
    .setColorCaptionLabel(0)
    ;
  cp5.addBang("rec")
    .setPosition(10, 130)
    .setSize(50, 20)
    .setColorCaptionLabel(0)
    ;
}


void divSquare(float x_pos, float y_pos, float wd){ //正方形の分割   
    float x_end_pos = x_pos + wd;
    float y_end_pos = y_pos + wd;
    while (wd > thr){
        itr++;
        if (itr %2 == 1){
            while (x_pos + wd*ratio <= x_end_pos){ //奇数回目はx軸方向に長方形を増やす
                fill(color(random(1), 1, 1));
                rect(x_pos + 5.0, y_pos + 5.0, wd*ratio, wd); //作画位置の調整
                div_rect(x_pos, y_pos, wd*ratio, wd); //正方形の分割
                x_pos += wd*ratio;
            }
            wd = x_end_pos - x_pos;
        }
        else {
            while (y_pos + wd/ratio <= y_end_pos){ //偶数回目はy軸方向に長方形を増やす
                fill(color(random(1), 1, 1));
                rect(x_pos + 5.0, y_pos + 5.0, wd, wd/ratio);
                div_rect(x_pos, y_pos, wd, wd/ratio); //正方形の分割
                y_pos += wd/ratio;
            }
            wd = y_end_pos - y_pos;
        }
    }
}


void div_rect(float x_pos, float y_pos, float x_wd, float y_wd){
    int itr = 0;
    float x_pos_sq = 0;
    float y_pos_sq = 0;
    float x_end = x_wd;
    float y_end = y_wd;
    float wd_sq = y_wd;

    //正方形の分割
    while (wd_sq > thr){
        itr++;
        if (itr %2 == 1){
            while ((x_pos_sq + wd_sq <= x_end)){ //奇数回目はx軸方向に正方形を増やす
                rect(x_pos_sq+ x_pos+5.0, y_pos_sq + y_pos+5.0, wd_sq, wd_sq); //作画位置の調整
                divSquare(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq);
                x_pos_sq += wd_sq;
            }
            wd_sq = x_end - x_pos_sq;
        }
        else {
            while ((y_pos_sq + wd_sq <= y_end)){ //偶数回目はy軸方向に正方形を増やす
                rect(x_pos_sq + x_pos + 5.0, y_pos_sq + y_pos + 5.0, wd_sq, wd_sq);
                divSquare(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq);
                y_pos_sq += wd_sq;
            }
            wd_sq = y_end - y_pos_sq;
        }
    }
}

分割時のx軸に基づいた色相分類

float num_A = 10;
float num_B = 6;
float ratio = (float) num_B/num_A;


// Parameters
float x_pos = 0;
float y_pos = 0;
int itr = 0;
float thr = 10;

void setup(){//いわゆるmain関数
    //描画
    size(410, 410); //windowサイズ
    colorMode(HSB, 1);
    float wd = width - 10;

    divSquare(x_pos, y_pos, wd); //正方形の分割
    
    save("Euclidean_recursive_rectangular_3_with_color.png");
}

void divSquare(float x_pos, float y_pos, float wd){ //正方形の分割    
    float x_end_pos = x_pos + wd;
    float y_end_pos = y_pos + wd;
    while (wd > thr){
        itr++;
        if (itr %2 == 1){
            while (x_pos + wd*ratio <= x_end_pos){ //奇数回目はx軸方向に長方形を増やす
                fill(color(1-x_pos/(width+x_pos), 1, 1));
                rect(x_pos + 5.0, y_pos + 5.0, wd*ratio, wd); //作画位置の調整
                div_rect(x_pos, y_pos, wd*ratio, wd); //正方形の分割
                x_pos += wd*ratio;
            }
            wd = x_end_pos - x_pos;
        }
        else {
            while (y_pos + wd/ratio <= y_end_pos){ //偶数回目はy軸方向に長方形を増やす
                fill(color(1-x_pos/(width+x_pos), 1, 1));
                rect(x_pos + 5.0, y_pos + 5.0, wd, wd/ratio);
                div_rect(x_pos, y_pos, wd, wd/ratio); //正方形の分割
                y_pos += wd/ratio;
            }
            wd = y_end_pos - y_pos;
        }
    }
}


void div_rect(float x_pos, float y_pos, float x_wd, float y_wd){
    int itr = 0;
    float x_pos_sq = 0;
    float y_pos_sq = 0;
    float x_end = x_wd;
    float y_end = y_wd;
    float wd_sq = y_wd;

    //正方形の分割
    while (wd_sq > thr){
        itr++;
        if (itr %2 == 1){
            while ((x_pos_sq + wd_sq <= x_end)){ //奇数回目はx軸方向に正方形を増やす
                rect(x_pos_sq+ x_pos+5.0, y_pos_sq + y_pos+5.0, wd_sq, wd_sq); //作画位置の調整
                divSquare(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq);
                x_pos_sq += wd_sq;
            }
            wd_sq = x_end - x_pos_sq;
        }
        else {
            while ((y_pos_sq + wd_sq <= y_end)){ //偶数回目はy軸方向に正方形を増やす
                rect(x_pos_sq + x_pos + 5.0, y_pos_sq + y_pos + 5.0, wd_sq, wd_sq);
                divSquare(x_pos_sq+ x_pos, y_pos_sq + y_pos, wd_sq);
                y_pos_sq += wd_sq;
            }
            wd_sq = y_end - y_pos_sq;
        }
    }
}

実行結果は以下、

Appendix: Processingによる色の指定

HSB色空間

色の三属性である色相(Hue)，彩度(Saturation・Chroma)，明度(Brightness・Value)で色を指定する色空間で，HSV色空間とも呼ばれます．RGB 表現が色の科学的な現象を元に指定するものであることに比べ，色の種類（色相）と鮮やかさと明るさという人間の感覚的な指標で指定ができるため，デザイナには好まれて使われます．

HSB 色空間における色相は，0°～360° の値を持ち，0 は赤，120 が緑，240 が青と定められています．HSV 色空間に限らず，色相を円状に配置したものを色相環と呼びますが，HSB色空間における色相環は次のようになります．

HSB色空間における明度は 0～100% で色の明るさを表し，各色相においてもっとも明るい色で 100% の値をとります．彩度も 0～100% の値をとり，この値が小さくなるほど色が褪せていきます．明度が小さい場合，彩度を変化させても色はあまり変わりません．色相が 0° のときの彩度と明度の組み合わせを表した図を下に示します．横軸が彩度で左端が 0% で右端が 100%，縦軸が明度で上端が 0% で下端が 100% です．

Processing における色の指定

Processing では，RGB 色空間と HSB 色空間を利用することができます．RGB 色空間を使いたい場合は RGB を，HSB 色空間を使いたい場合は HSB をパラメータとして colorMode メソッドを呼び出します．

colorMode( RGB );
colorMode( HSB );

また，RGB においては赤，緑，青の度合，HSB においては色相，彩度，明度を，どのような範囲の数値で指定するかを設定することもできます．

colorMode(HSB, 1);

とすれば、HSBのそれぞれの度合を 0～1 の値で設定できます．

colorMode( HSB, 100, 10, 10 );

とすれば，実際は0～359°の色相を 0～99，0～100%の彩度と明度を 0～10 で設定できるようになります．

Share Buttons
Share on:

Feature Tags
Leave a Comment
(注意：GitHub Accountが必要となります）

1. ユークリッド互除法とは？

ユークリッド互除法

ユークリッド互除法の実装

ユークリッドの互除法の証明

2. 拡張ユークリッド互除法

不定方程式の定理

証明

ユークリッド互除法の一次不定方程式への応用

3. Processingを用いたユークリッド互除法の可視化

ユークリッド互除法を用いた長方形の分割

色をつける場合

長方形による正方形の分割

長方形による長方形の分割

4. 再帰的分割

長方形を正方形に分割して再度長方形に分割する

正方形の再帰的分割

GUIでパラメーター調整

分割時のx軸に基づいた色相分類

Appendix: Processingによる色の指定

HSB色空間

Processing における色の指定

CONTENTS