| 概要 | |
|---|---|
| 目的 | 調和級数, オイラーの定理, ゼータ関数のメモ |
| 参考 | - 素数物語 アイディアの饗宴 (岩波科学ライブラリー) - 高校数学の美しい物語 > 調和級数が発散することの3通りの証明 |
調和級数
\(\zeta(p) = \sum_{k = 1}^{\infty} \frac{1}{k^p}\) をリーマンのゼータ関数といいます。\(\zeta(p)\)は調和級数(harmonic sequence)と呼ばれます。調和級数は発散することが知られています。以下で、調和級数が発散することを証明します。(→参考:高校数学の美しい物語)
ニコール・オレムの証明
\[\begin{aligned} \zeta(1) &= \sum_{k = 1}^{\infty} \frac{1}{k}\\ &= 1 + \frac{1}{2} + \left(\frac{1}{3} + \frac{1}{4}\right) + \left(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)+\cdots\\ &> 1 + \frac{1}{2} + \left(\frac{1}{4} + \frac{1}{4}\right) + \left(\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}\right)+\cdots\\ &= 1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots \end{aligned}\]となり、\(1/2\)が限りなく加わるので。帳は級数は発散する。
■
指数関数のマクローリン型不等式を用いた証明
\[\begin{aligned} &\exp\left(1 + \frac{1}{2} + \frac{1}{3} + \cdots +\frac{1}{n}\right)\\ &=\exp\left(1\right) \exp\left(\frac{1}{2}\right)\exp\left(\frac{1}{3}\right) \cdots \exp\left(\frac{1}{n}\right)\\ &\geq (1 + 1)\left(1 + \frac{1}{2}\right)\left(1+\frac{1}{3}\right)\cdots \left(1+\frac{1}{n}\right) \: \because \text{マクローリン展開}\\ &= 2\cdot \frac{3}{2}\cdot \frac{4}{3}\cdot \frac{5}{4}\cdots \cdot \frac{n+1}{n}\\ &= n+1 \end{aligned}\]よって、
\[\sum_{k = 1}^{n} \frac{1}{k} \geq \log(n+1)\]\(n\to \infty\)とすると右辺は発散するので左辺も発散する
■
積分を用いる方法
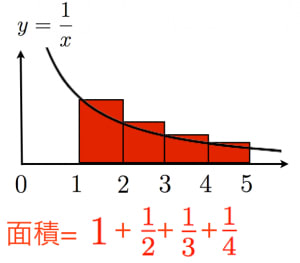
図より、
\[\sum_{k=1}^n > \int_{1}^{n+1}\frac{1}{x}dx = \log(n+1)\]\(n\to \infty\)とすると右辺は発散するので左辺も発散する
■
対数近似
上の証明と同様の証明により
\[\log(n+1) < \sum_{k=1}^n \frac{1}{n} < 1 + \log(n)\]とわかります。よって, \(n\)が十分大きいとき,
\[\sum_{k=1}^n \frac{1}{n} \approx \log n\]コンプガチャの期待値
調和級数に関連する確率の問題として、コンプガチャの期待値があります。
問題設定
- 1回ガチャを行うと,\(n\) 種類の景品のうち1種類の景品がもらえる。
- どの景品が当たる確率も等確率,つまり \(\dfrac{1}{n}\) である。同じ景品が何回も連続することもある。
コンプガチャの期待値
\(n\) 種類,等確率のコンプガチャで全ての景品を集めるのに必要な回数の期待値は
\[n(1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots +\dfrac{1}{n})\]証明: 期待値の線形性
\(k\) 種類持っている状態から新たに1種類ゲットするまでにかかる回数を \(X_k\) (確率変数)とおきます。
もとめる期待値は
\[N=E[X_0+X_1+\cdots +X_{n-1}]\]ここで期待値の線形性より
\[N=\sum_{k=0}^{n-1}E[X_k]\]\(X_k = m\)となる確率は、\(m-1\)回失敗して次に成功する確率なので、
\[\left(\frac{k}{n}\right)^{m-1}\left(1 - \frac{k}{n}\right)\]よって、
\[E[X_k] = \sum_{m=1}^\infty m \left(\frac{k}{n}\right)^{m-1}\left(1 - \frac{k}{n}\right)\]等比×等差の和を参考に計算すると、
\[E[X_k] = \frac{1}{1 - (k/n)} = \frac{n}{n-k}\] \[\therefore N = \sum_{k=1}^{n-1}\frac{n}{n-k} = n\sum_{k=1}^{n}(\frac{1}{k})\]■
\(n\) が十分大きいとき, 調和級数コンプガチャの回数の期待値はおよそ \(n\log n\) 回であると言えます。
ブールの不等式とコンプガチャの確率
命題
n 種類のコンプガチャ(景品は全て等確率)を \(2n\log n\) 回引いてもコンプリートできない確率は \(\dfrac{1}{n}\) 以下。
補助定理: どれか一つでも起きる確率はそれぞれが起きる確率の和よりも小さい
事象 \(A_1,A_2,\cdots,A_n\) に対して
\[P(A_1\cup A_2\cup\cdots\cup A_n)\leq \sum_{i=1}^nP(A_i)\]各事象が互いに排反なら等号が成立します。
証明
\(2n\log n\) 回引いても \(k\) 番目の種類のガチャが一回も当たらない確率を \(A_k\) とおきます。
コンプリートできない確率は \(P(A_1\cup \cdots\cup A_n)\) であるが,これはブールの不等式より
\[P(A_1\cup \cdots\cup A_n) < \sum_{k=1}^nP(A_k) = nP(A_1)\]ここで、
\[\begin{aligned} P(A_1) &= \left(\frac{n-1}{n}\right)^{2n\log n}\\ &= \left[\dfrac{1}{\left(1 - \frac{1}{n}\right)^{-n}}\right]^{\log n^2}\\ &\leq \frac{1}{e^{\log n^2}}\\ & = \frac{1}{n^2} \end{aligned}\] \[\therefore P(A_1\cup \cdots\cup A_n) < \frac{1}{n}\]■
オイラーの定理
定理
素数を表す集合を\(\mathbf P\)と定義する。
\[\sum_{p\in\mathbf P}\frac{1}{p} \:\text{ と }\: \prod_{p\in\mathbf P}\frac{1}{1 - \frac{1}{p}}\]は発散する。
証明
\(x\geq 2\)となる実績\(x\)に対して、
\[\begin{aligned} S(x) &= \sum_{p\leq x, p\in \mathbf P}\frac{1}{p}\\ P(x) &= \prod_{p\leq x, p\in \mathbf P}(1 - 1/p)^{-1} \end{aligned}\]と定義します。\(2^m > x\)なる自然数mをとります。
\[(1 - 1/p)^{-1} = \sum_{n=0}^\infty (1/p)^n\]なので、
\[P(x) = \prod_{p\leq x, p\in \mathbf P}(1 - 1/p)^{-1} > \prod_{p\leq x, p\in \mathbf P} \left(1 + \frac{1}{p} + \frac{1}{p^2} + \cdots + \frac{1}{p^m}\right) \tag{A}\]\(m\)のとり方から、\(x\)以下の自然数はすべて(A)の分母に現れるので、
\[P(x) > \sum_{n\leq x}\frac{1}{n}\tag{B}\](B)は\(x\to \infty\)のとき発散するので、\(P(x)\)も\(x\to \infty\)のとき発散する。
つぎに、\(S(x)\)が\(x\to \infty\)のとき発散することを示す。\(\log(1 - t)\)のマクローリン展開より、\(t \in (0, 1)\)に対して、
\[\log(1 - t) + t = -\frac{t^2}{2}-\frac{t^3}{3}-\frac{t^4}{4} - \cdots \tag{C}\](C)の右辺を変形すると
\[\begin{align*} -\frac{t^2}{2}-\frac{t^3}{3}-\frac{t^4}{4} - \cdots &> -\frac{t^2}{2}-\frac{t^3}{2}-\frac{t^4}{2} - \cdots\\ &= -\frac{t^2}{2(1 - t)} \tag{D} \end{align*}\](D)の結果を用いて、
\[\begin{align*} \log P(x) - S(x) &= -\sum_p \log \left(1 - \frac{1}{p}\right) - \sum_p \frac{1}{p}\\ &= -\sum_p \left\{\log \left(1 - \frac{1}{p}\right) + \frac{1}{p}\right\}\\ &< \sum_{p}\frac{1}{2p^2(1-1/p)}\\ &= \sum_p \frac{1}{2p(p-1)}\\ &< \sum_{n=2}^\infty \frac{1}{2n(n-1)} = \frac{1}{2}\sum_{n=2}^\infty \left(\frac{1}{n-1} - \frac{1}{n}\right)\\ &= \frac{1}{2} \end{align*}\] \[\therefore S(x) > \log(P(x)) - \frac{1}{2} \tag{E}\](E)の左辺は\(x\to \infty\)のとき発散するので、\(S(x)\)も\(x\to \infty\)のとき発散する。
■
オイラー積
\[\sum_{n = 1}^{\infty}\frac{1}{n^s} = \prod_{p \in \mathbf P} \frac{1}{1 - \frac{1}{p^s}}\]定理
\[\frac{1}{1 - \frac{1}{p^s}} = 1 + \frac{1}{p^s} + \frac{1}{p^{2s}} + \frac{1}{p^{3s}} + \cdots\]証明
別の素数 \(q\)についても
\[\frac{1}{1 - \frac{1}{q^s}} = 1 + \frac{1}{q^s} + \frac{1}{q^{2s}} + \frac{1}{q^{3s}} + \cdots\]となり、これを掛け合わせると、各項には\(p, q\)を素因数とする自然数のs乗が分母に現れます。素因数分解の一意性より、
\[\prod_{p \in \mathbf P} \frac{1}{1 - \frac{1}{p^s}}\]の各項にはすべての自然数のs乗が分母に表れるので、
\[\sum_{n = 1}^{\infty}\frac{1}{n^s} = \prod_{p \in \mathbf P} \frac{1}{1 - \frac{1}{p^s}}\]■
リーマンのゼータ関数
\[\zeta(s) = \sum_{n=1}^\infty n^{-s}\]定理
は、\(s > 1\)のとき収束し、\(0 < s \leq 1\)のとき発散する。
証明
\(s> 1, t > 1\) のとき \(1/t^s\)は単調減少だから、
\[\int^{n+1}_n \frac{1}{t^s}dt < \frac{1}{n^2} < \int^{n}_{n-1} \frac{1}{t^s}dt\] \[\therefore \: \sum_{2\leq n \leq k}\frac{1}{n^s} < \int^{k}_1\frac{1}{t^s}dt < \int^{\infty}_1\frac{1}{t^s}dt = \left[\frac{t^{1-s}}{1-s}\right]^{\infty}_1 = \frac{1}{s-1}\]従って、上に有界だから単調増加関数である正項級数は収束する。
\(s = 1\)のとき、\(\zeta(1)\)は発散するので、\(s < 1\)の場合も同様に発散する。
■
Appendix
等比×等差の和
\[\sum_{m=1}^\infty m \left(\frac{k}{n}\right)^{m-1} \: \text{ where } \: \frac{k}{n}\in (0, 1)\]を求めたいとします。単純化のため,
\[r = \frac{k}{n}\]とおき、問題を以下のように変形します。
\[S = \sum_{m=1}^\infty m r^{m-1} = 1 + 2r + 3r^2 + \cdots\]両辺に\(r\)を掛けると、
\[rS = r + 2r^2 + 3r^3 + \cdots\]よって、
\[\begin{aligned} S - rS &= 1 + r + r^2 + \cdots\\ &= \sum_{k=0}^\infty r^{k} \\ &= \frac{1}{1-r} \end{aligned}\]従って、
\[S = \frac{1}{(1 - r)^2}\]を得ます。\(r = \frac{k}{n}\)より、
\[\sum_{m=1}^\infty m \left(\frac{k}{n}\right)^{m-1} = \frac{1}{(1 - k/n)^2}\]■
(注意:GitHub Accountが必要となります)