巴戦の確率

	概要
目的	巴戦の勝利確率と公平な巴戦の検討
参考	-高校数学の美しい物語 -28年東大前期理数学.pdf

巴戦の問題
PythonでSimution
公平な巴戦の検討
- 問題設定
- $x$ の導出
4人の巴戦

巴戦の問題

Ａ、Ｂ、Ｃの３人の力士で試合を行う。１試合目は、Ａ対Ｂで行い、次の試合からは、勝者が待機していた残りの１人と試合を行う。２回連続して勝てば優勝であり、誰かが優勝するまで繰り返す。Ａ、Ｂ、Ｃのいずれも、各試合で勝つ確率が５割であるとする。

(1) A, B, Cのそれぞれの優勝確率を求めよ
(2) $n$ を 2以上の整数とする。ちょうど $n$ 試合目でAが優勝する確率を求めよ。
(3) 優勝が決定するまで必要な試合数の期待値を求めよ
(4) $m$ を正の整数とする。総試合数が $3m$ 回以下でAが優勝したとき、Aの最後の対戦相手がBである条件付確率を求めよ
(5) 優勝が決定するまで必要な試合数の分散を求めよ

解答(1)

対戦して負けた力士が優勝する確率を$p$とおく。

A, Bが優勝する確率

最初の2試合で連続して勝利して優勝するパターン
最初の試合で勝利し、2試合目に負けて、それ以降で優勝するパターン
最初の試合に負けて, それ以降で優勝するパターン

\[\frac{1}{2}\times \frac{1}{2} + \frac{1}{2}\times p + \frac{1}{2}\times \frac{1}{2} \times p = \frac{1}{4} + \frac{3}{4}p\]

Cが優勝する確率

2試合目と3試合目に連続して勝利して優勝するパターン
2試合目に勝って,3試合目に負けて、3試合目の勝者が4試合目に負けるという条件のもとそれ以降で優勝するパターン

\[\frac{1}{2}\times \frac{1}{2} + \frac{1}{2}\times \frac{1}{2}\times　p = \frac{1}{4} + \frac{1}{4}p\]

各力士が優勝する事象の和集合は全事象、かつ排反事象なので、A, B, Cのそれぞれの優勝する確率を合計すると1になる。

\[\frac{3}{4} + \frac{7}{4}p = 1\] \[\therefore p = \frac{1}{7}\]

よって、

\[\begin{aligned} Pr(\text{Aが優勝する確率}) &= \frac{5}{14}\\ Pr(\text{Bが優勝する確率}) &= \frac{5}{14}\\ Pr(\text{Cが優勝する確率}) &= \frac{2}{7}\\ \end{aligned}\]

■

解答(1)別解

Aが $n$ 試合目に優勝する確率を $a_n$ とする。 $a_1=0$ ，$a_2=\frac{1}{4}$ ，$a_3=0$, $a_4 = \frac{1}{16}$. これを$n\geq 2$について整理すると

初戦に勝った場合、$n= 3k+2 (k = 0, 1, 2, ....)$回目に優勝する. また、B, Cがそれまで2連勝しない場合に限るので, $a_n = \frac{1}{2^n}$
初戦に負けた場合、$n= 3k+1 (k = 1, 2, ....)$回目に優勝する. また、B, Cがそれまで2連勝しない場合に限るので, $a_n = \frac{1}{2^n}$
$3k$ 回目の試合には出ることはないので$a_{n} = 0 \text{ s.t. } n = 3$

よって、Aの優勝する確率は

\[\sum_{n=2}^\infty a_n = \frac{\frac{1}{4}}{1 - \frac{1}{2}} - \frac{\frac{1}{8}}{1 - \frac{1}{8}} = \frac{5}{14}\]

Bの優勝確率も同様に計算できる。

Cがn回目に優勝する確率を$c_n$とする。

$n= 3k+1 (k = 0, 1, 2, ....)$回目に優勝することはできない, そもそも出番がない
$n= 3k+2 (k = 0, 1, 2, ....)$回目に優勝することはできない, 試合をしたとしてもそれは1戦目
$n = 3k (k = 1, 2, ....)$回目に優勝する確率は$a_n = \frac{1}{2^{n-1}}$

よって、Cの優勝する確率は

\[\sum_{n=1}^\infty c_n = \frac{\frac{1}{4}}{1 - \frac{1}{8}} = \frac{2}{7}\]

もちろん、

\[\sum_{n=1}^\infty c_n = 1 - 2\sum_{n=1}^\infty a_n\]

で計算しても良い.

■

解答(2)

解答(1)の別解を参照。

■

解答(3)

優勝に要する試合数の確率変数を$X$.
A, B, Cがそれぞれ優勝する事象は排反
$a_n, b_n, c_n$は $n$回目の試合でA, B, Cが優勝する確率
\[a_n = b_n\]

このとき、優勝に要する試合数の期待値は

\[\mathbf E[X] = \sum_{n = 2}^{\infty}n(a_n + b_n + c_n) = \sum_{n = 2}^{\infty}n(2a_n + c_n)\]

と表せる。

このとき、解答(1)の別解より

\[2a_n = \begin{cases} \frac{1}{2^{n-1}} &\text{ if } n \text{ は３の倍数ではない}\\[8pt] 0 &\text{ if } n \text{ は３の倍数} \end{cases}\]

かつ

\[c_n = \begin{cases} \frac{1}{2^{n-1}} &\text{if } n \text{ は３の倍数}\\[8pt] 0 &\text{if } n \text{ は３の倍数ではない} \end{cases}\]

なので、

$d_n = \frac{1}{2^{n-1}}$とすると

\[\therefore \mathbf E[X] = \sum_{n = 2}^{\infty}nd_n = \sum_{n = 1}^{\infty}n\frac{1}{2^{n-1}}- 1 = 3\]

■

解答(3)別解

A対CでAが勝てばチャンピオンが決まるし，Cが勝ってもA，B，Cの立場が入れ替わるだけで状況は変わらないことを考えると，これから先の何戦目くらいでチャンピオンが決まるかという数値を$r$とすれば

\[r＝1＋r/2\]

が成り立つ. 従って,$r＝2$が求まる。結局，これに最初にA，B，Cが決まるまでの1戦を加えて対戦回数の期待値は3。

■

解答(4)

解答(1)別解より、Aが優勝するときにBが対戦相手のときは、$n= 3k+1 \:(k = 1, 2, ....)$のときのみ。

求めたいものは

\[\text{Pr(Bが対戦相手|3m回以内にAが優勝)} = \frac{\text{Pr(3m回以内にAが優勝, Bが対戦相手)}}{\text{Pr(3m回以内にAが優勝)}}\]

各項について、

\[\begin{aligned} \text{Pr(3m回以内にAが優勝)} &= \sum_{m=1}^{3m}a_n\\ &= \sum_{m=2}^{3m}\frac{1}{2^m} - \sum_{m=1}^{m}\frac{1}{2^{3m}}\\ &= \frac{1}{2} - \frac{1}{2^{3m}} - \frac{1}{7}\left(1 - \frac{1}{8^m}\right)\\ &= \frac{5}{14} - \frac{6}{7}\frac{1}{8^m} \end{aligned}\]

および

\[\begin{aligned} \text{Pr(3m回以内にAが優勝, Bが対戦相手)} &= \sum_{m=1}^{m-1} a_{3m+1}\\ &= \sum_{m=1}^{m-1} \frac{1}{2^{3m+1}}\\ &= \frac{1}{14} - \frac{4}{7}\frac{1}{8^m} \end{aligned}\]

総試合数が $3m$ 回以下でAが優勝したとき,Bが対戦相手である確率を $B_m$とすると

\[\begin{aligned} \therefore B_m &= \frac{ \frac{1}{14} -\frac{4}{7\cdot 8^m} }{ \frac{5}{14} -\frac{6}{7\cdot 8^m} } \\[8pt] &= \frac{ 8^m -8 }{ 5\cdot 8^m -12 } \end{aligned}\]

■

解答(5)

$p \in (0, 1)$のとき、

\[\frac{1}{(1-p)^2}=\sum_{x=1}^\infty xp^{x-1}\]

この両辺を$p$で微分すると

\[\frac{2}{(1-p)^3}=\sum_{x=2}^\infty x(x-1)p^{x-2}\]

両辺に$p$を掛けると

\[\frac{2p}{(1-p)^3}=\sum_{x=2}^\infty x(x-1)p^{x-1}\]

優勝に要する試合数の確率変数を$X$をしたとき

\[\mathbf V(X) = \mathbf E[X(X - 1)] + E(X) - E(X)^2\]

従って、

\[\begin{aligned} \mathbf V(X) &= \sum_{x=2}^\infty x(x-1)\frac{1}{2^{x-1}} + 3 - 9\\ &= \frac{1}{(1/2)^3} - 6\\[8pt] &= 2 \end{aligned}\]

■

PythonでSimution

実行ファイルはこちら

modules

import numpy as np
import random
import matplotlib.pyplot as plt

関数定義

def tomoesen(player_list, iter_num, seed = 42):
    
    ## set seed
    random.seed(seed)

    ## set object
    winner_cnt = {player:[0] for player in player_list}
    max_win = len(player_list) - 1

    for trial in range(iter_num):
        winner = ""
        battle = player_list[:2]
        waiting_list = player_list[2:]
        win_cnt = 0

        while win_cnt < max_win:
          _winner, _loser = random.sample(battle, 2)

          if winner == _winner:
            win_cnt += 1

          else:
            win_cnt = 1
            winner = _winner
          
          waiting_list.append(_loser)
          battle = [winner, waiting_list.pop(0)]
        
        other_set = set(player_list) - set(winner)

        ## updateting the result
        winner_cnt[winner].append(winner_cnt[winner][-1] + 1)
        for other in other_set:
          winner_cnt[other].append(winner_cnt[other][-1])
    
    return winner_cnt

Simulation

## simulation回数
N = 100000
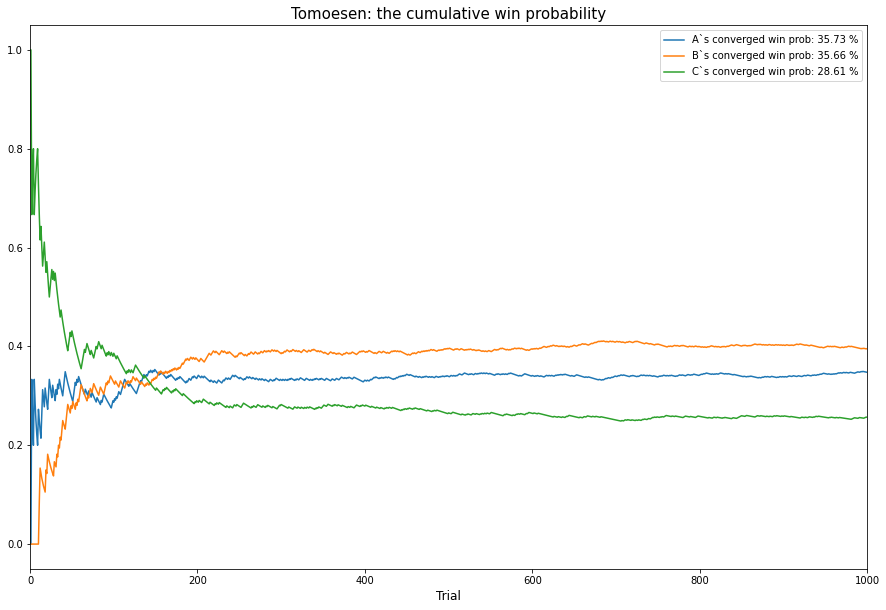
result = tomoesen(player_list = list('ABC'), iter_num=N)

fig, ax = plt.subplots(1, 1,figsize=(15, 10))
trial_range = np.arange(1, N+1)

for player in sorted(result.keys()):
  win_prob = result[player][1:]/trial_range
  ax.plot(win_prob,label = (player + '`s converged win prob: {} %').format(round(win_prob[-1]*100, 2)))

ax.set_title('Tomoesen: the cumulative win probability', fontsize=15)
ax.set_xlabel('Trial', fontsize=12)
ax.set_xlim(0, 1000)
ax.legend();

公平な巴戦の検討

上では実力が均等な場合の巴戦を検討しました. ここでは、巴戦による優勝確率が３プレーヤーとも公平, つまり $\frac{1}{3}$になるための条件を検討します.

問題設定

３人のプレイヤーをA, B, Cとする
まず最初にA, Bが土俵に上がり、その後、その勝者とCが戦い、優勝が決定する（だれかが2連勝する）までゲームを続ける
A, Bの実力は均等とする

２つ目までの条件は上で検討した設定と同様です. ３つ目の条件をもう少し説明すると

\[\begin{aligned} Pr(\text{AがBと戦い勝利する}) &= \frac{1}{2}\\ Pr(\text{BがAと戦い勝利する}) &= \frac{1}{2}\\ Pr(\text{AがCと戦い勝利する}) &= Pr(\text{BがCと戦い勝利する}) = x \end{aligned}\]

今回求めたいのは巴戦で優勝する確率が各プレイヤー公平になるためには $x$ がどのような水準でなければならないのか？です.

$x$ の導出

問題設定より、

$Pr(\text{Aが優勝する}) = Pr(\text{Bが優勝する}) = Pr(\text{Cが優勝する}) = \frac{1}{3}$

解答(1)の別解を応用して、

Aが初戦勝って、優勝する確率
Aが初戦負けて、優勝する確率

をそれぞれ検討し、その後 $Pr(\text{Aが優勝する})$を導出したいと思います.

Aが初戦勝って、優勝する確率

$a_n$ をAが初戦勝って、$n$戦目に優勝する確率とします. (i, j)を i と j が対戦して, iが勝った事象を表すとします.

$a_2$: (A, B) (A, C)
$a_5$: (A, B) (C, A) (B, C) (A, B) (A, C)
$a_8$: (A, B) (C, A) (B, C) (A, B) (C, A) (B, C) (A, B)(A, C)

なので、

\[a_{3k-1} = \left\{\frac{(1-x) x}{2}\right\}^{k-1} \frac{1}{2} \times x \: \text{ where } \:(k \geq 1)\]

Aが初戦負けて、優勝する確率

$b_n$ をAが初戦勝って、$n$戦目に優勝する確率とします.

$b_4$: (B, A) (C, B) (A, C) (A, B)
$b_7$: (B, A) (C, B) (A, C) (B, A) (C, B) (A, C) (A, B)
$b_{10}$: (B, A) (C, B) (A, C) (B, A) (C, B) (A, C) (B, A) (C, B) (A, C) (A, B)

なので、

\[\begin{aligned} b_{3k+1} &= \frac{1}{2} \left\{(1 - x) x \frac{1}{2}\right\}^{k-1} (1 - x) x \frac{1}{2}\\ &= \frac{ (1 - x) x }{4}\left\{\frac{(1 - x) x}{2}\right\}^{k-1} \: \text{ where } \: (k \geq 1) \end{aligned}\]

Aが優勝する確率

\[\begin{aligned} Pr(\text{Aが優勝する}) = \sum^{\infty}_{n = 1} a_{3n - 1} + b_{3n + 1} \end{aligned}\]

なので

\[Pr(\text{Aが優勝する}) = \frac{1}{2}\left(\frac{x}{1 - \frac{1}{2}(1 - x)x} + \frac{(1-x)x}{2(1 - \frac{1}{2}(1 - x)x)}\right)= \frac{1}{3}\]

これを整理すると

\[0 = 5x^2 - 11x +4\]

を得るので、$(0, 1)$区間に収まるほうが $x$となり得るので

\[x = \frac{11 - \sqrt{41}}{10}\]

この値を用いて、PythonでSimulationを実施した結果は以下：

■

4人の巴戦

問題

$n \:(n = 4)$人が巴戦を行う時、それぞれの優勝する確率を求めよ. $n$ 人が一列に並んでいて、先頭の二人が勝負をして勝った方が先頭に残る．負けた方は列の最後につく．これを繰り返して $n - 1$ 連勝したとき優勝するとします.

解

$k$ 連勝している人が先頭にいるときの $m$ 番目にいる人の優勝する確率を $P_{k;m}とおきます．$P_{0; 1},P_{0; 2}, \cdots, P_{0; 4}$$を求めることが最終目標です

$k=3$ のときは先頭の人がすでに3連勝しているので

\[\begin{aligned} P_{3; 1} &= 1\\ P_{3; 2} &= P_{3; 3} = P_{3; 4} = 0 \end{aligned}\]

また、先頭の2人は実力が拮抗しており、試合チャンスも同じなので、$P_{0, 1} = P_{0, 2}$.

$k \: (0\leq k\leq 2)$ 連勝しているとき、先頭の2人は

\[\begin{aligned} P_{k; 1} &= \frac{1}{2}(P_{k+1; 1} + P_{1; n})\\[8pt] P_{k; 2} &= \frac{1}{2}(P_{1; 1} + P_{k+1; n}) \end{aligned}\]

3番目以降の人は

\[P_{k; m} = \frac{1}{2}(P_{k+1; m-1} + P_{1; m-1})\]

漸化式を整理すると、

\[\begin{aligned} P_{k;1} &= 2P_{k-1;1} - P_{1; n}\\[8pt] P_{k;m} &= 2P_{k-1; m+1} - P_{1;m} \: (2 \leq m \leq n-1)\\[8pt] P_{k;n} &= 2P_{k-1;2} - P_{1; 1} \end{aligned}\]

今回は $n=4$ なので上の漸化式を利用すると

\[\begin{aligned} P_{1;1} &= \frac{3}{4}P_{1;4} + \frac{1}{4}\\ P_{1;2} &= \frac{1}{2}(P_{1;1} + P_{1;3})\\ P_{1;3} &= \frac{1}{2}P_{1;2} + \frac{1}{4}P_{1;1}\\ P_{1;4} &= \frac{1}{2}P_{1;3} + \frac{1}{4}P_{1;2} \end{aligned}\]

この連立方程式を解くと

\[\begin{aligned} P_{1;1} &= \frac{56}{149}\\ P_{1;2} &= \frac{36}{149}\\ P_{1;3} &= \frac{32}{149}\\ P_{1;4} &= \frac{25}{149} \end{aligned}\]

従って、

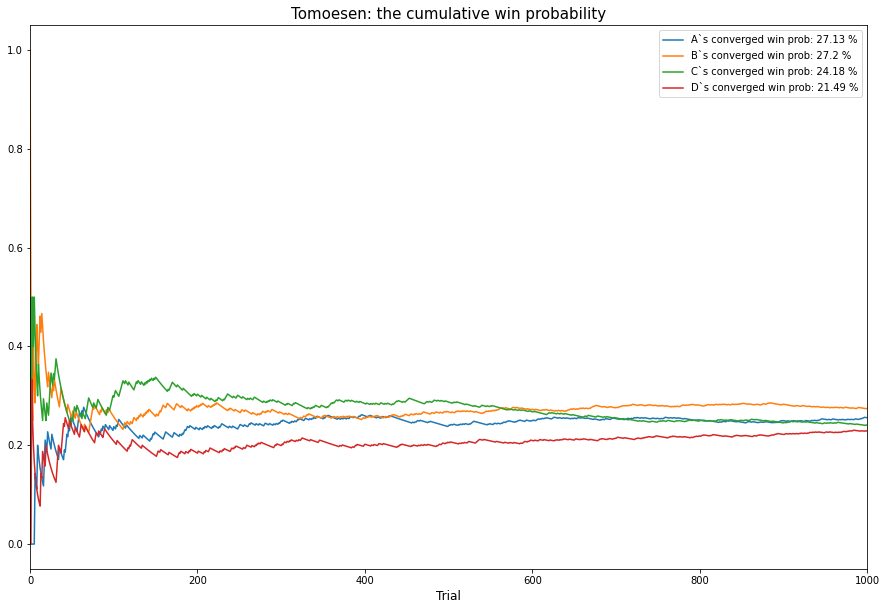
\[\begin{aligned} P_{0;1} &= P_{0;2} = \frac{81}{298}\\ P_{0;3} &= \frac{36}{149}\\ P_{0;4} &= \frac{32}{149}\ \end{aligned}\]

■

PythonでのSimulation

一般解

$n \: (n\geq 3)$ 人で巴戦を実施する場合の各プレイヤーの優勝確率は

\[\begin{aligned} P_{0, 1} &= P_{0, 2}\\[8pt] P_{0, m} &= \frac{2^{(n-1)(m-2)}(2^{n-1}+1)^{n-m}}{2(2^{n-2}+1)(2^{n-1}+1)^{n-2} - 2^{(n-1)^2}}\: \text{ where }\: (2 \leq m \leq n)\\[8pt] \sum_{i=1}^n P_{0, i} &= 1 \end{aligned}\]

となります. 考え方は上で紹介した確率漸化式を解くのですが、余因子行列をコネコネする必要があるので解説は後日とします.

また優勝がきまるまでの試合数 $T$ の期待値は

\[\mathbf E[T] = 2^{n-1} - 1\]

となります.

Share Buttons
Share on:

Feature Tags
Leave a Comment
(注意：GitHub Accountが必要となります）

巴戦の勝利確率と公平な巴戦の検討

巴戦の問題

解答(1)

解答(1)別解

解答(2)

解答(3)

解答(3)別解

解答(4)

解答(5)

PythonでSimution

公平な巴戦の検討

問題設定

\(x\) の導出

4人の巴戦

CONTENTS