| 概要 | |
|---|---|
| 目的 | 二項係数とGauss hypergeometric function |
| 参考 | - Wolfram alpha: 二項分布の累積分布関数の近似式 - scipy.special.hyp2f1: Gauss hypergeometric function 2F1(a, b; c; z) |
公平なコインを投げた場合
問題
公平なコインを2人が \(n\) 回ずつ投げる時、表が同じ回数ずつ出る確率を求めよ
解答
プレイヤーをA, Bと表現する時、プレイヤー \(i \in \{A, B\}\) が表を出す回数を \(X_i\)という確率変数で表すと \(X_i\)は独立に二項分布 \(\mathrm{B}(n, 0.5)\)に従います. 従って、
\(Pr(X_i = k) = \:_nC_k \left(\frac{1}{2}\right)^{k}\left(\frac{1}{2}\right)^{n-k} = \:_nC_k \left(\frac{1}{2}\right)^{n}\)
従って、求めるべき確率は
\(\begin{aligned} \sum_{k=0}^n Pr(X_A = k, X_B = k) &= \sum_{k=0}^n Pr(X_A = k)^2\\ &= \sum_{k=0}^n \:_nC_k \:_nC_k \left(\frac{1}{2}\right)^{2n}\\ &= \sum_{k=0}^n \:_nC_k \:_nC_{n-k} \left(\frac{1}{2}\right)^{2n}\\ &= \:_{2n}C_n\left(\frac{1}{2}\right)^{2n} \end{aligned}\)
■
Pythonでsimulation
上で考えた問題について、コインを投げる回数を10~50回のレンジでそれぞれ1万回ずつ実験してみます。上で得られた理論値と実験で得られる結果を比較してみます.
module
1
2
3
import random
import matplotlib.pyplot as plt
import scipy.special as sc
関数の定義
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def flip_coin(n, p):
"""
Return
表がでる確率が p のコインを n回投げた時、表が出る回数
Paramters
n: trial
p: success rate
"""
res = sum([1 if random.random() < p else 0 for i in range(n)])
return res
def coin_flip_sample(n_sample, n, p):
"""
Return
二人のプレイヤーがそれぞれ独立にn回coin flipをして、同じ回数表が出た場合 1 そうでない場合 0がでる実験を考える
n_sample回実験を繰り返した時、同じ回数表が出た割合を返す
Paramters
n_sample: 実験回数
n: trial
p: success rate
"""
data = []
for t in range(n_sample):
coin_a = flip_coin(n, p)
coin_b = flip_coin(n, p)
data.append(1 if coin_a == coin_b else 0)
return sum(data)/n_sample
実験結果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
### simulation version 1
res = []
p_true = 0.5
for n_trial in range(10, 50):
p_sample = coin_flip_sample(n_sample = 10000, n = n_trial, p = p_true)
p_theory = p_true**(2*n_trial)*sc.comb(2*n_trial, n_trial)
res.append([p_theory, p_sample])
plt.figure(figsize = (10, 10))
plt.scatter(*zip(*res))
plt.xlabel('True probability', fontsize = 20)
plt.ylabel('Sample probability', fontsize = 20)
plt.title("Compare the theory-based and sample probability", fontsize = 20);

不公平なコインを投げた場合
上で考えた問題を一般化し、表が出る確率が \(p\) となるコインの場合を考えてみます.このとき、2人の表の回数が一致する確率は
\[Pr(X_i = k) = \:_nC_k p^{k}(1-p)^{n-k}\]より
\(\begin{aligned} \sum_{k=0}^n Pr(X_A = k, X_B = k) &= \sum_{k=0}^nPr(X_A = k)^2\\ &= \sum_{k=0}^n \:_nC_k \:_nC_{n-k} p^{2k}(1-p)^{2n-2k}\\ &= (1 - p)^{2 n} \:_2F_1\left(-n, -n, 1, \frac{p^2}{(p - 1)^2}\right) \end{aligned}\)
なお、\(_2F_1(a, b; c; x)\)は the gauss hypergeometric functionです.
Pythonで確認
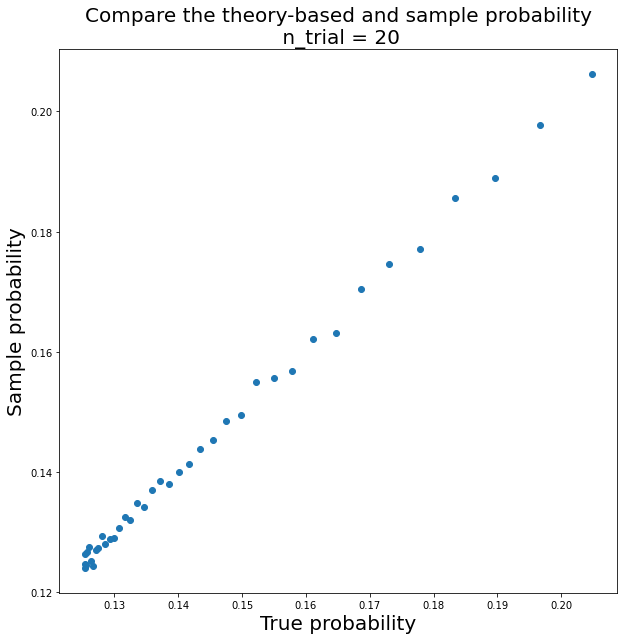
\(p\)の値を0.1から0.5のレンジでstep 0.01で動かしてsimulationしてみます.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
### simulation version 2
res = []
n_trial = 20
p_range = np.linspace(0, 0.5, 51)[10:]
for p_true in p_range:
hyper_geometric_4th = (p_true/(p_true - 1))**2
p_theory = (1 - p_true)**(2*n_trial)*sc.hyp2f1(-n_trial, -n_trial, 1, hyper_geometric_4th)
p_sample = coin_flip_sample(n_sample = 100000, n = n_trial, p = p_true)
res.append([p_theory, p_sample])
plt.figure(figsize = (10, 10))
plt.scatter(*zip(*res))
plt.xlabel('True probability', fontsize = 20)
plt.ylabel('Sample probability', fontsize = 20)
plt.title("Compare the theory-based and sample probability\n n_trial = 20", fontsize = 20);
(注意:GitHub Accountが必要となります)