Table of Contents
問題:一様分布の変数変換
確率変数 $X, Y$が独立に $\text{Unif}(0, 1)$に従っているとき、$Z= X + Y$, $W = XY$の確率密度関数を求めよ
(1) $Z= X + Y$の確率密度関数
$Z$のpdfは
\[f_Z(z) = \int^1_0f_X(z-t)f_Y(t)dt\]となります. $0<z-t<1$, $0<t<1$より$z\in (0, 1)$のときは$t$の積分範囲は$(0, z)$. また$z\in (1, 2)$のときは積分範囲が$(z-1, 1)$になることに留意すると
\[f_Z(z) = \begin{cases}\int^z_0 dt = z & \ \ z\in (0, 1) \\ \int^1_{z-1} dt = 2-z & \ \ z\in (1, 2) \end{cases}\]直感的なイメージ
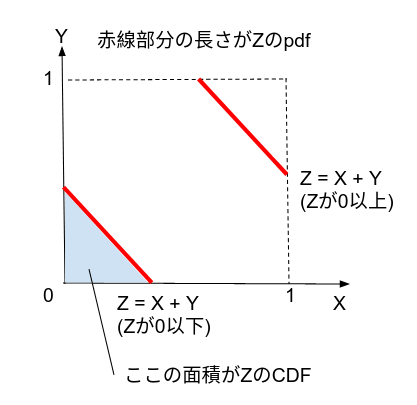
$Z$の値によって積分範囲がかわるイメージはこの図を参照することでわかります. $Z$のCDFは$X, Y \in [0, 1]$で画定された四角形のうち$X + Y$の等高線を引き、その線分と原点から伸びる$X, Y$方面それぞれの線分で囲まれた領域となります. pdfはその面積の増分、つまり等高線の赤線部分となるので、$Z = 1$を境界に変わることがわかります.
(2) $W = XY$の確率密度関数
\[\begin{align*} W & = XY\\ U & = X \end{align*}\]と変数変換すると$J((w, u)\to (x, y)) = 1/u$となります. 従って、
\[f_{W, U}(w, u) = u^{-1}I(u \in (0, 1))I(w/u \in (0, 1))\]これを$u\in(0,1)$範囲で積分すると
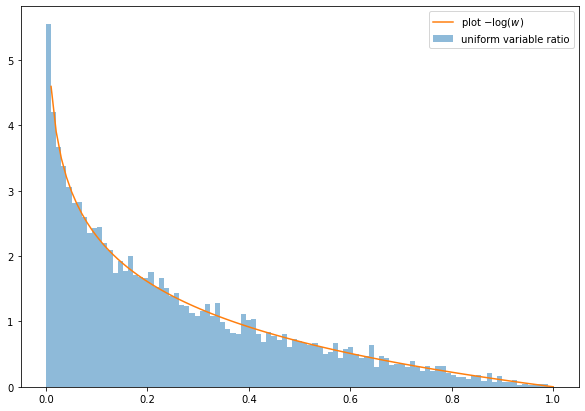
\[\begin{align*} f(w) &= \int^1_0 u^{-1}I(u \in (0, 1))I(w/u \in (0, 1)) du\\ &= \int^1_0 u^{-1}I(w/u \in (0, 1)) du\\ &= \int^1_0 u^{-1}I(w<u) du\\ &= \int^1_w u^{-1} du\\ &= -\log w \end{align*}\]Pythonでplot
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
## SEED
np.random.seed(42)
## Params
N = 10000 #sample size
A, B = 0, 1 # uniform distribution param
## generate random variables
X = np.random.uniform(A, B, N)
Y = np.random.uniform(A, B, N)
W = X*Y
## plot parameter
bin_range = np.linspace(A, B, 100)
fig, ax = plt.subplots(1, 1,figsize=(10, 7))
ax.hist(W, density = True, alpha = 0.5, bins = bin_range, label = 'uniform variable ratio')
ax.plot(bin_range[1:], -np.log(bin_range[1:]), label = 'plot $-\log(w)$')
ax.legend();
2. 円周上で一様分布する点の此の距離:統計検定1級2013年11月
周の長さ1の円の円周上に1点Aを固定し、次に、同じ円周上で一様分布するように別の点Bをとる. その二点で区切られてできる2つの弧ABのうち短い方の長さをX, 長い方の長さをYとする.
- $X$及び$Y$の期待値と標準偏差を求めよ. また、$X, Y$の相関係数も求めよ
- $W=X/Y$の累積分布関数と確率密度関数を求めよ
- $W$の期待値と中央値を求めよ
(1) $X$及び$Y$の期待値と分散を求めよ. また、$X, Y$の相関係数も求めよ
$X$は区間$(0, 0.5)$の一様分布に従い、$Y = 1 - X$より$Y$は区間$(0.5, 1)$の一様分布に従う. 従って、
\[\begin{align*} E[X] &= \frac{0 + 0.5}{2} = 0.25\\ V(X) &= \frac{(0.5 - 0)^2}{12} = \frac{1}{48}\\ E[Y] &= \frac{0.5 + 1}{2} = 0.75\\ V(Y) &= \frac{(1 - 0.5)^2}{12} = \frac{1}{48}\\ Corr(X, Y) &= \frac{cov(X, Y)}{\sqrt{V(X)V(Y)}} = -1 \end{align*}\](2) $W=X/Y$の累積分布関数と確率密度関数を求めよ
$X$のCDFは$x\in (0, 0.5)$の範囲で$F(x) = 2x$なので、$W = X/Y$は$w\in (0, 1)$の範囲で
\[\begin{align*} F(w) &= F\left(\frac{X}{1-X}\leq w\right)\\ &= F\left(X\leq\frac{w}{1+w}\right)\\ &= 2 - \frac{2}{1+w} \end{align*}\]確率密度関数は、CDFを$w$で微分すれば良いので
\[f(w) = \frac{2}{(1 + w)^2}\]\[\begin{align*} \mathrm E[W] &= \int^1_0\frac{2}{(1 + w)^2}wdw\\ &= \int^1_0\frac{2(1 + w) - 2}{(1 + w)^2}dw\\ &= \int^1_0\frac{2}{(1+w)}dw - \int^1_0\frac{2}{(1+w)^2}dw\\ &= [2\log(1+w)]^1_0 + \left[\frac{2}{1+w}\right]^1_0\\ &= 2\log 2 - 1 \end{align*}\](3) $W$の期待値と中央値を求めよ
中央値は
\[\begin{align*} &2 - \frac{2}{1+\tilde w} = 0.5\\ &\Rightarrow \tilde w = \frac{1}{3} \end{align*}\]3. 一様分布と順序統計量: 統計検定1級2012年11月
累積分布関数が標準一様分布に従う証明
連続型確率変数$Z$の累積分布関数$F(z) = Pr(Z\leq z)$が狭義単調増加であるとき、$U=F(Z)$は標準一様分布に従うことが知られています.
証明
確率変数$U$の累積分布関数を$G(u)$とすると、$u\in (0, 1)$に対して、
\[\begin{align*} G(u) &= Pr(U\leq u)\\ &= Pr(F(Z)\leq u)\\ &= Pr(Z\leq F^{-1}(u))\\ &= F(F^{-1}(u))\\ &= u \end{align*}\]従って、$u\in (0, 1)$に対して$G(u)=u$は標準一様分布の累積分布関数なので題意が示された.
順序統計量と特性値
$U_1, U_2, U_3$を互いに独立に標準一様分布に従う確率変数とします. このとき、$X_1$を最も小さいもの、$X_2$を二番目に小さいもの、$X_3$を最も大きいものとします. $X_1, X_2, X_3$それぞれの確率密度関数と期待値を求めたいとします
まず簡単な$X_3$の累積分布関数を導出します.
\[\begin{align*} F_3(x)& = Pr(\max(U_1, U_3, U_3)\leq x)\\ &= Pr(U_1\leq x)Pr(U_2\leq x)Pr(U_3\leq x)\\ &= x^3 \end{align*}\]従って、確率密度関数は$f_3(x) = 3x^2$. また期待値は
\[\begin{align*} \mathrm E[X_3] &= \int^1_0 3x^3dx\\ &= \frac{3}{4}[X^4]^1_0\\ &= \frac{3}{4} \end{align*}\]次に$X_1$の累積分布関数を導出します.
\[F_1(x) &= Pr(\min(U_1, U_3, U_3)\leq x)\\ &= 1 - Pr(\min(U_1, U_3, U_3)> x)\\ &= 1 - (1 - Pr(U_1 > x))(1 - Pr(U_2 > x))(1 - Pr(U_3 > x))\\ &= 1 - (1-x)^3\]従って、確率密度関数は$f_1(x) = 3(1-x)^2$. また期待値は
\[\begin{align*} \mathrm E[X_1] &= \int^1_0 3x(1-x)^2dx\\ &= \frac{1}{4} \end{align*}\]最後に$X_2$の累積分布関数を導出します. $X_2$については確率要素を用いて確率密度関数を導出します. $X_2$の確率要素を
\[f_2(x)dx \approx Pr(x < X_2 < x+dx)\]とすると、$dx$よりも高位の無限小を無視すると
\[\begin{align*} f_2(x)dx &\approx Pr(x < X_2 < x+dx)\\ &= Pr(U_{(1)} < x)Pr(x < U_{(2)} < x+dx)Pr(U_{(1)} > x + dx)\\ &= 3x\times 2dx \times (1-x)\\ &=6x(1-x)dx \end{align*}\]従って確率密度関数は$f_2(x) = 6x(1-x)$. 期待値は$\frac{1}{2}$.
REMARKS
一般的に、一様分布に従う確率変数が$m$個あるとき、小さい方から$k$番目の変数$X_k$の期待値は
\[\mathrm E[X_k] = \frac{k}{m+1}\]関連記事
References
(注意:GitHub Accountが必要となります)