Table of Contents
問題設定
あなたはある店舗のマネージャーで、その店舗と同一地域に住む住民がその店舗へ年間来店する回数を知りたいとします. 調査方法として、とある1日をピックアップして、その時来店したお客様全員に「年間何回来店するか?」というアンケートを考えました.
前提
- 人々は独立に来店するとする
- 人々の来店回数は同一の分布に従うとする(例:二項分布やポワソン分布)
- アンケートの回答率は100%とする
- 1日1回までしか来店しないとする
どのようなバイアスが含まれるのか?
「とある1日をピックアップして、その時来店したお客様にアンケートをとる」場合、アンケートサンプルに含まれる人は
- 来店回数が1回以上の人
- 来店回数が多いほど、アンケートサンプルに含まれやすい
という問題が考えられます. 「来店回数が多いほど、アンケートサンプルに含まれやすい」とは年間1回しか来店しない人がアンケートサンプルに含まれる確率は $1/365$ ですが毎日来店する人は確率 1 でアンケートサンプルに含まれるのが直感的説明です.
バイアスをどのようの補正するか?
「来店回数が多いほど、アンケートサンプルに含まれやすい」ので、来店回数を確率変数 $X$ としたとき、その$X$に応じて「アンケートサンプルに含まれる確率」を定式化することが考えられます.
- $g(x)$: 各個人アンケートサンプルに含まれる確率関数(pmf)
- $f(x)$: 各個人の来店回数の確率関数(pmf)
とすると
\[\begin{align*} g(x) &= \frac{xf(x|X>0)}{\sum xf(x|X>0)}\\ &= \frac{xf(x|X>0)}{E[X|X>0]} \quad\quad\tag{1} \end{align*}\]分子の$xf(x|X>0)$は$X = x$である人がサンプルに含まれる相対比率を表現しています. また分母で$\sum xf(x|X>0)$が出てくる理由は$\sum g(x) = 1$を担保するためです.
推定:二項分布とポワソン分布で確認する
二項分布のパラメータを推定する
二項分布は $X\sim B(N, p)$としたとき
\[f(x) = \frac{\Gamma(N+1)}{\Gamma(N-x+1)\Gamma(x+1)}p^x(1-p)^{N-x}\]と表現されます. (1)に基づき、$g(x)$を計算するために$f(x|X>0)$と$E[X|X>0]$を計算する必要があります. $F(X)$を$f(x)$に対応する累積分布関数とすると
\(\begin{align*} f(x|X> 0) &= \frac{f(x)}{1 - F(X = 0)}\\ &= \frac{\Gamma(N+1)}{\Gamma(N-x+1)\Gamma(x+1)}p^x(1-p)^{N-x} / (1 - (1-p)^N) \end{align*}\)
\(\begin{align*} E[X|X>0] &= \sum^N_{x=1} xf(x|X> 0)\\ &= \sum^N_{x=1} \frac{x}{(1 - (1-p)^N)}\frac{\Gamma(N+1)}{\Gamma(N-x+1)\Gamma(x+1)}p^x(1-p)^{N-x}\\ &= \sum^N_{x=0} \frac{x}{(1 - (1-p)^N)}\frac{\Gamma(N+1)}{\Gamma(N-x+1)\Gamma(x+1)}p^x(1-p)^{N-x}\\ &= \frac{Np}{(1 - (1-p)^N)} \end{align*}\)
従って、(1)と照らし合わせて
\[g(x) = \frac{\Gamma(N)}{\Gamma(N - x + 1)\Gamma(x)}p^{x-1}(1-p)^{N-x}\]よって、アンケートサンプルに基づく来店回数の期待値は $x’ = x - 1$とすると
\[\begin{align*} \sum x g(x) &= \sum x\frac{\Gamma(N)}{\Gamma(N - x + 1)\Gamma(x)}p^{x-1}(1-p)^{N-x}\\ &= \sum (x'+1)\frac{\Gamma(N)}{\Gamma(N-x')\Gamma(x'+1)}p^{x'}(1-p)^{N-x'-1}\\ &= \sum (N-1)p + 1 \end{align*}\]今回は$N = 365$なのでアンケートサンプルに基づく来店回数を$\bar Y$とすると
\[\hat P = \frac{\bar Y - 1}{365 - 1}\]と推定することができる.
Python Simulation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
## SEED
np.random.seed(42)
## Params
N = 365 #年間日数
P = 0.1 #来店確率
M = 10000 #地域住民人数
survey_index = 100 #調査日
simulation_cnt = 100 #simulation回数
def binary_search(func, y_min, y_max, value, eps):
left = y_min # left seach area
right = y_max # right seach area
while left <= right:
mid = (left + right) / 2 # calculate the mid
if abs(func(mid) - value) < eps:
# return the numerical solution
return mid
elif func(mid) < value:
# set the left at the mid beacuse the objective function is a strictly increasing function
left = mid
else:
# set the right at the mid
right = mid
return None # cannot compute
def objective_function(x):
return 365*x/(1 - (1 - x)**365)
def adjusted_estimator(bar_y):
return (bar_y - 1) / (365 - 1)
def plot_simulation(data, label, ax = None):
if ax is None:
fig, ax = plt.subplots(1, 1,figsize=(10, 7))
ax.hist(data, density = True, alpha = 0.5, bins = np.linspace(P/1.05, P*1.05, 50), label = label)
ax.set_xlabel('estimate distribution', fontsize=12)
ax.set_ylabel('density', fontsize=12)
ax.legend()
bias_result = []
adj_result = []
for iter_cnt in range(simulation_cnt):
data = stats.bernoulli.rvs(P, size=(N, M))
data = data * np.sum(data, axis = 0)
sampling_data = data[100, :]
sampling_data = sampling_data[sampling_data > 0]
bar_y = np.mean(sampling_data)
bias_estimate = binary_search(func=objective_function, y_min=0, y_max =1, value = bar_y, eps = 1e-8)
adj_estimate = adjusted_estimator(bar_y)
bias_result.append(bias_estimate)
adj_result.append(adj_estimate)
fig, ax = plt.subplots(1, 1,figsize=(10, 7))
plot_simulation(bias_result , label='conditional-$E[X|X>0]$', ax=ax)
plot_simulation(adj_result , label='Adjusted-estimator', ax=ax)
ax.set_title('Compare each estimator results: bias-p = {:.4f}, adj-p={:.4f}'.format(np.mean(bias_result), np.mean(adj_result)), fontsize=15);
bias_mape = np.mean(abs((np.array(bias_result) - P)/P))
adj_mape = np.mean(abs((np.array(adj_result) - P)/P))
print(bias_mape, adj_mape)
>>> 0.024919937638333015 0.0037611339049107738
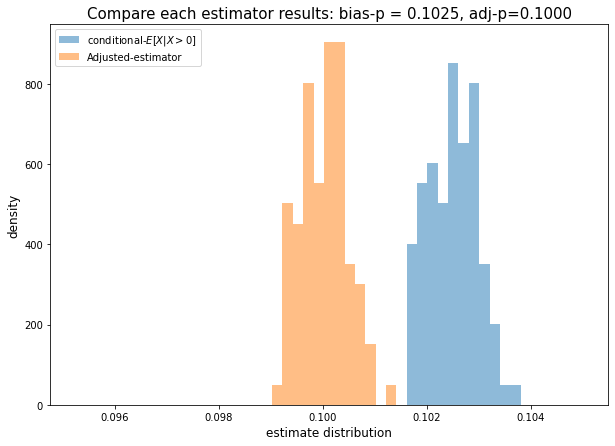
- MAPEを比較すると誤差はまあまあ大きいことがわかる
ポワソン分布のパラメータを推定する
二項分布の場合と同様にポワソン分布における$g(x)$を表現すると
\[g(x) = \frac{\lambda^{x-1}\exp(-\lambda)}{\Gamma(x)}\]となり、$Poisson(\lambda)$に従う確率変数を$Y$としたとき, $X = Y+1$, $g(x) = f(y)$と表現することがわかる(REMARKS: これは二項分布のときも同様).
従って、
\[\begin{align*} &\sum x g(x) = \lambda + 1\\ &\sum x^2 g(x) - (\sum x g(x))^2 = \lambda \end{align*}\]となる. 二項分布の場合と同様に看過できないupward-biasが存在することがわかる.
この分析手法の応用
- Internal validityが保証されたAB Test実施時も、そこで得られたATEが必ずしもPATEとは一致しない問題が発生するのは多々あります
- 実験ATEをPATE推定値に変換する際に、AB Testサンプリングの確率の計算をすることで上述の分析手法によるバイアス補正に応用できます(treatment effectのheterogeneityを暗に仮定してますが…)
(注意:GitHub Accountが必要となります)