Table of Contents
- 問題: 2回連続で表が出る確率
- 問題:$k$回連続で表が出るまでのコイン投げ回数の期待値
- 問題: 交互にサーブを行う時に、2点差つけることができる確率
- 問題: 交互に2回ずつサーブを行う時に、2点差つけることができる確率
- References
問題: 2回連続で表が出る確率
表の出る確率が$p$のコインを$n$回続けて投げる時、表が続けては現れない確率を$q_n$とする.
- $q_n$に関する漸化式を求めよ
- pが$2/3$のとき、$q_n$をnの関数として求めよ
(1) $q_n$に関する漸化式を求めよ
$q_n$に該当する事象は「$n$回目に表が出るが表は2回連続で表れることはない」事象と「$n$回目に裏が出るが表は2回連続で表れることはない」事象に分けて考えることができます. 従って、
\(\begin{align*} q_n = (1 - p)q_{n-1} + p(1-p)q_{n-2} \quad\quad\tag{1.1} \end{align*}\)
また、$q_0 = q_1 = 1$となります.
(2) pが$2/3$のとき、$q_n$をnの関数として求めよ
pが$2/3$のとき, (1.1)は以下のようになる:
\[q_n = \frac{1}{3}q_{n-1} + \frac{1}{3}\frac{2}{3}q_{n-1}\]従って、
\[\begin{align*} q_n - \frac{2}{3} &= -\frac{1}{3}\left(q_{n-1} - \frac{2}{3}q_{n-2}\right)\\ q_n + \frac{1}{3} &= \frac{2}{3}\left(q_{n-1} + \frac{1}{3}q_{n-2}\right) \end{align*}\]更に整理すると
\[\begin{align*} q_n - \frac{2}{3} &= \left(-\frac{1}{3}\right)^{n-1}\frac{1}{3}\\ q_n + \frac{1}{3} &= \left(\frac{2}{3}\right)^{n-1}\frac{4}{3} \end{align*}\]以上より、
\[q_n = (-1)^{n-1}\left(\frac{1}{3}\right)^{n+1} + 2 \left(\frac{2}{3}\right)^{n+1}\]$p$についての一般解について
ここはWolfram alphaさんのお力をお借りしました…
\[A \equiv \sqrt{-3p^2 + 2p + 1}\]とすると
\[\begin{align*} q_n =& \frac{1}{A}2^{-n-1}\\[8pt] & \left[-p(-A - p + 1)^n + (A - 1)(-A - p + 1)^n + (p + A + 1)(A - p + 1)^n\right] \end{align*}\]これに対して、$p=2/3$を代入すると$A = 1$となり計算しやすくなり
\[q_n\left(\frac{2}{3}\right) = (-1)^{n+1}\left(\frac{1}{3}\right)^{n+1} + 2 \left(\frac{2}{3}\right)^{n+1}\]問題:$k$回連続で表が出るまでのコイン投げ回数の期待値
表の出る確率が$p$のコインを投げ続け、$k$回連続で表がでるまでの回数を$n$としたとき、この$N$の期待値を求めよ.
解答
まず、$k=4$で探索的に調べてみます. 表が$z$回連続で出たとし,連続4回になるまでにあと何回くらいコインを投げるかという期待値を$x_z$で表すとします.
状態$Z=z$のとき、追加でコインを一回投げると確率$p$で$z+1$の状態へ遷移、$1-p$で$Z=0$へ遷移することに着目すると期待値は以下のように表せます.
\[\begin{align*} x_0 &= 1 + p x_1 + (1-p)x_0\\[8pt] x_1 &= 1 + p x_2 + (1-p)x_0\\[8pt] x_2 &= 1 + p x_3 + (1-p)x_0\\[8pt] x_3 &= 1 + (1-p)x_0 \end{align*}\]従って、これを連立させて解くと
\[x_0 = \left(\frac{1}{1-p}\right)\left(\frac{1}{p^4}-1\right)\]次に、一般化して$k$回連続して表が得られたら終了とする場合、期待値の連立方程式は
\[\begin{align*} x_0 &= 1 + p x_1 + (1-p)x_0\\[8pt] x_1 &= 1 + p x_2 + (1-p)x_0\\[8pt] \vdots&\\ x_{k-2} &= 1 + p x_{k+1} + (1-p)x_0\\[8pt] x_{k-1} &= 1 + (1-p)x_0 \end{align*}\]なので
\[\begin{align*} x_0 &= \left(\frac{1}{1-p}\right)\left(\frac{1}{p^k}-1\right)\\[8pt] x_{k-1} &= \frac{1}{p^k}\\ x_{z} &= 1 + \sum_{i=z}^{k-1}\frac{1}{p^{i+1}} \end{align*}\]と表現できます. なお、$p=1/2$のときは
\[x_0 = 2(2^k - 1)\]と覚えやすく求めることができます.
MGFを用いてコイン投げ回数の分散を求める
次にコイン投げ回数$N$の分散を求めたいとします. まず $N<k$ の範囲では$P(N < k) = 0$となります. また、$P(N = k) = p^k$も自明です.
次に、$N > k$の場合を考えます. この場合、最後の$k+1$回の試行は裏1回表$k$回なので, $n>k$としたとき
\[P(N = n) = (1 - P(N < N-k-1))(1-p)p^k\]次に、MGFを定義します
\[\begin{align*} E[\exp(tN)] &= \sum_{n=0}^\infty\exp(tn)P(N=n)\\[8pt] &= \exp(tk)p^k + (1 - p)p^k\sum_{n=k+1}^\infty \exp(tn)P(N > n - k - 1)\\[8pt] &= \exp(tk)p^k + (1 - p)p^k\sum_{n=k+1}^\infty \exp(tn)\sum_{z=n-k}^\infty P(N=z)\\[8pt] &= \exp(tk)p^k + (1 - p)p^k\sum_{n=k+1}^\infty\sum_{z=n-k}^\infty \exp(tn)P(N=z)\\[8pt] &= \exp(tk)p^k + (1 - p)p^k\sum_{z=1}^\infty\sum_{n=k+1}^{k+z} \exp(tn)P(N=z)\\[8pt] &= \exp(tk)p^k + (1 - p)p^k\sum_{z=1}^\infty P(N=z) \frac{\exp(t(k+1)) - \exp(t(k+z+1)}{1 - \exp(t)}\\[8pt] &= \exp(tk)p^k + (1 - p)p^k\frac{\exp(t(k+1))}{1 - \exp(t)}(1 - E[\exp(tN)]) \end{align*}\]あとはこれを整理し、$E[N^2]$ を計算すれば良いだけになります. なおこれの計算は手間がかかるので$p=1/2$のケースを考えてみたいと思います.
\[E[\exp(tN)|p=1/2] = \frac{\exp((k+1)t) - 2\exp(tk)}{2^{k+1}(\exp(t)-1) - \exp((k+1)t)}\]従って、分散は
\[\begin{align*} V(N) &= E[N^2] - E[N]^2\\[8pt] &= 2 (-2^{k + 1} k - 2^k + 2^{2 k + 1} - 1) \end{align*}\]問題: 交互にサーブを行う時に、2点差つけることができる確率
実力が拮抗しているA, Bの二人が、卓球をすることにした. ルールは交互にサーブをし、先に相手よりも2点差つけたプレイヤーが勝ちとします. 2人は実力が拮抗しているため、どちらもサーブをした時の勝率は等しく $p$ だとします. このとき、先にサーブをした人が有利なのかどうか確認せよ
解答
先にサーブする人の勝率を$P_1$とします. 先手の勝利パターンを分類すると
- 初回サーブに勝利 & 次の後手のサーブもブレイク
- 初回サーブは勝利 & 次の後手のサーブはブレイク失敗 & 初期状態に戻る
- 初回サーブはブレイクされる & 次の後手のサーブはブレイク成功 & 初期状態に戻る
の3つに分けることができます. 従って、
\[\begin{align*} P_1 &= p(1-p) + ppP_1 + (1-p)(1-p)P_1\\[8pt] &\Rightarrow P_1 = \frac{1}{2} \end{align*}\]従って、先行有利はこの問題設定上は存在しない.
問題: 交互に2回ずつサーブを行う時に、2点差つけることができる確率
実力が拮抗しているA, Bの二人が、今度はテニスのデュースで勝負するにした. ルールは交互に2回ずつサーブをし、先に相手よりも2点差つけたプレイヤーが勝ちとします. 2人は実力が拮抗しているため、どちらもサーブをした時の勝率は等しく $p$ だとします. このとき、先にサーブをした人が有利なのかどうか確認せよ.
解答
今回どのような状態があり得るか整理します.
- 自分がサーブで、アドバンテージなしの状態
- 自分がサーブで、アドバンテージありの状態
- 自分がサーブで、相手にアドバンテージありの状態
- 相手がサーブで、アドバンテージなしの状態
- 相手がサーブで、自分にアドバンテージありの状態
- 相手がサーブで、相手にアドバンテージありの状態
ここで、確率変数$S$を自分がサーブの時1, 相手がサーブの時0と定義します. また確率変数$X$を自分のアドバンテージのポイントを示す変数とします(相手にアドバンテージがある場合は$X = -1$).
このとき状態$(s, x)$ごとに今回のゲームに勝利する確率を$P(s, x)$とすると、
\[\begin{align*} P(1, 0) &= p\times P(1,1) + (1-p)\times P(1,1)\\[8pt] P(1, 1) &= p + (1-p)\times P(0,0)= p + (1-p)\times (1- P(1,0))\\[8pt] P(1, -1) &= p\times P(0,0) = p\times (1 - P(1,0)) \end{align*}\]なお途中の式展開は今回は2人の実力が拮抗しているので以下の等式が成り立つことを利用しています
\[\begin{align*} P(0,0) &= 1 - P(1, 0) \end{align*}\]従って、上述の連立方程式を解くと
\[P(1, 0) = \frac{2p(1-p) + p^2}{2p(1-p) + 1}\]$p=1/2$のときは先手後手の有利はないが
\[\begin{cases} \text{先手有利} & \ \ \text{ if }\ \ p> \frac{1}{2}\\[8pt] \text{後手有利} & \ \ \text{ if }\ \ p< \frac{1}{2} \end{cases}\]優勝決定までゲーム数の期待値
優勝決定のゲーム数は偶数しかありえないことに留意して書き出してみると
| ゲーム数 | 確率 |
|---|---|
| 2 | $p^2 + (1-p)^2$ |
| 4 | $(p^2 + (1-p)^2)(2p(1-p))$ |
| 6 | $(p^2 + (1-p)^2)(2p(1-p))^2$ |
| 8 | $(p^2 + (1-p)^2)(2p(1-p))^3$ |
従って、優勝決定までゲーム数を表す確率変数を$X$とすると, $2p(1-p) < 1$であることに留意すると
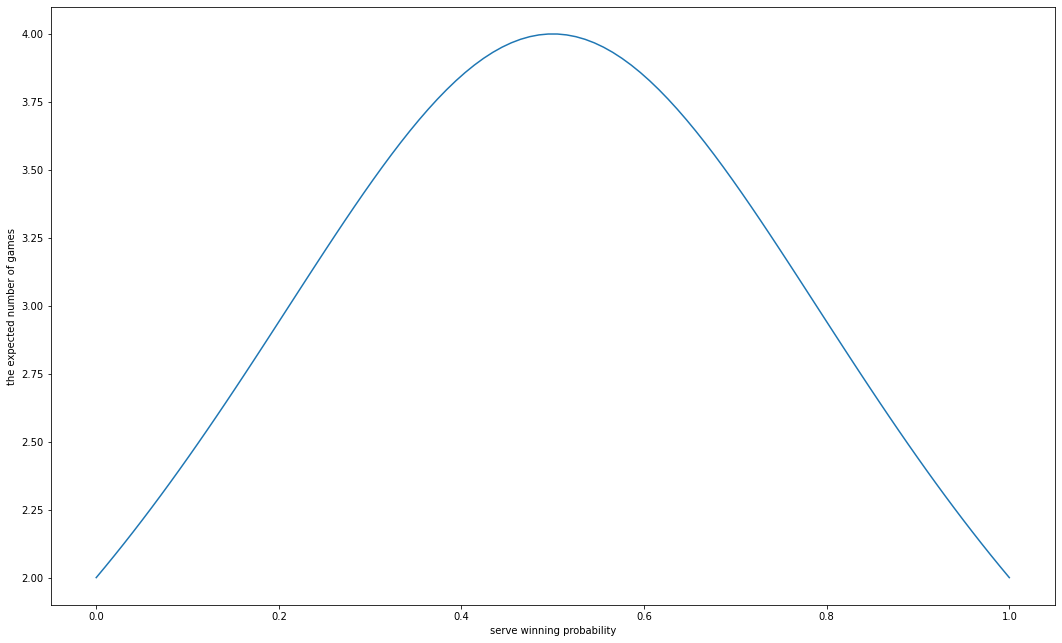
\[\begin{align*} E[X] &= \sum_{k=1}^\infty 2k(p^2 + (1-p)^2)(2p(1-p))^{k-1}\\ &= \frac{2(p^2 + (1-p)^2)}{[1 - 2p(1-p)]^2} \end{align*}\]$p = 1/2$のとき最大値を取り、$E[X|p = 1/2] = 4$ということがわかる. また、これをplotすると
1
2
3
4
5
6
7
8
9
10
import numpy as np
import matplotlib.pyplot as plt
p = np.linspace(0, 1, 100)
result = 2* (p**2 + (1-p)**2)/(1 - 2 * p * (1 - p))**2
plt.figure(figsize= (18, 11))
plt.plot(p, result)
plt.xlabel('serve winning probability')
plt.ylabel('the expected number of games')
References
- Ryo’s Tech Blog > 死神とのコイントスゲーム
- Ryo’s Tech Blog > 巴戦の確率
- Ryo’s Tech Blog > ベルヌーイ試行と二進数
- Ryo’s Tech Blog > マルコフ過程 一橋1992年
- Wolframalpha > 漸化式
(注意:GitHub Accountが必要となります)