Table of Contents
- 1. 微分方程式の基礎
- 2. 微分方程式を用いたCOVID-19 SEIRモデルの作成
- 3. モデルの拡張: $R_0$の水準に応じた死者と累積感染者数
- Ryo’s Tech Blog 関連記事
- References
1. 微分方程式の基礎
変数の導関数を含む方程式を「微分方程式」、特に独立変数が1つだけ存在する微分方程式を常微分方程式といいます. 1階の線形状微分方程式の例として、
\[\begin{align*} a_1\dot y(t) + a_2 y(t) + x(t) = 0 \ \ \text{ where } \dot y = \frac{dy(t)}{t} \tag{1.1} \end{align*}\]定常均衡
(1.1)式をベースに定常均衡という概念を紹介します. 定常均衡とは動学変数の変化が止まる状態を指します. (1.1)だと
\[\begin{align*} y(t) &= -\frac{1}{a_2}x(t)\\ &\Rightarrow\dot y = 0 \end{align*}\]定常均衡にはの安定/不安定の2つのケースがあります. 以下、具体例で紹介します.
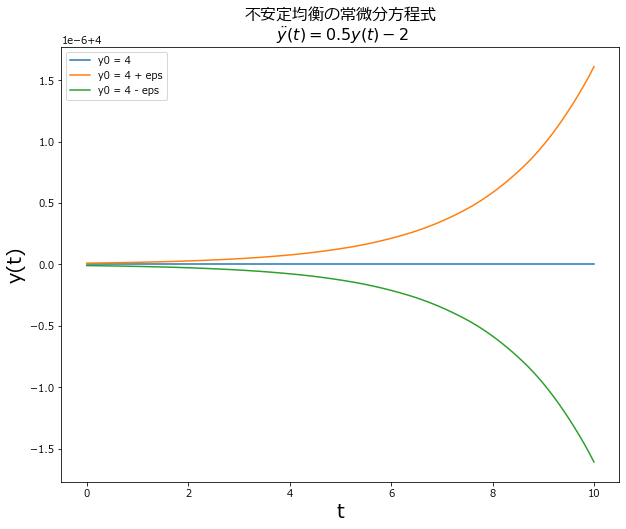
\[\begin{align*} \dot y(t) = 0.5 y(t) - 2 \end{align*}\]安定的/不安定な定常均衡
という微分方程式を考えます. このときの定常状態は$y^* = 4$ですが、ここで$\epsilon > 0$だけ定常状態からずれるケースを見てみると
\[\begin{align*} \dot y(t) &= 0.5 (4 + \epsilon) - 2\\ &= 0.5\epsilon > 0 \end{align*}\]したがって、ちょっとでも均衡状態からずれてしまうと$\dot y(t) > 0$より$y^*=4$から離れ続けてしまうことがわかります. 逆に
\[\begin{align*} \dot y(t) = -0.5 y(t) + 2 \end{align*}\]だとちょっとでも均衡状態からずれてしまっても $-0.5\epsilon < 0$より$y^*=4$へ戻ることがわかります.
不安定均衡をPython確認
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from scipy.integrate import odeint
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
def pend(y, t, a, b):
dydt = a * y - b
return dydt
## パラメーターの設定
a = 0.5
b = 2
eps = 1e-8
y0 = [4, 4 + eps, 4 - eps]
t = np.linspace(0, 10, 101)
## computation
sol = odeint(pend, y0, t, args=(a, b))
## plot
fig,ax = plt.subplots(figsize=(10,8))
ax.plot(t, sol[:, 0],label = 'y0 = 4')
ax.plot(t, sol[:, 1],label = 'y0 = 4 + eps')
ax.plot(t, sol[:, 2],label = 'y0 = 4 - eps')
ax.legend()
ax.set_title('不安定均衡の常微分方程式\n $\dot y(t) = {}y(t) - {}$'.format(a, b), fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('y(t)', fontsize=20)
2. 微分方程式を用いたCOVID-19 SEIRモデルの作成
SEIR (Susceptible-Exposed-Infected-Removed) という区分を用いたCOVID-19感染モデルの紹介をします.
解き明かしたいこと
- ソーシャルディスタンスの程度は感染拡大の程度にどれくらいの影響を及ぼすのか?
- 1時点での感染者の程度はどれくらいの見積もりになるのか?(現在の病床数で十分カバーされる範囲内か?)
The SEIR Modelの設定
状態のついて
SEIRモデルでは、人は4つの状態をS→E→I→Rの順番で変化していくと仮定します
- Susceptible: 未感染者
- Exoposed: 未発症の感染者
- Infected: 発症者
- Recovered: 免疫獲得者
状態遷移について
- 分析期間における人口は十分大きな水準$N$と一定とする,i.e., $N = S(t) + E(t) + I(t) + R(t)$
- 人口の遷移はSEIRの4つ以外は考えない
- $\beta(t)$: 感染率, S→Eの遷移の因子, ソーシャルディスタンスや移動制限によってこの値が変化します
- $\delta$: 発症率, E→I
- $\gamma$: 免疫獲得率, I→R
- 外生的stochastic shockによる各状態人数への影響は考えないものとする

$gamma$とポワソン過程
the Infected状態からthe Recovered状態への遷移を表す$\gamma$はポワソン過程が想定されるケースが多いです. この仮定のもとでは、発症から回復までの平均日数が$1/\gamma$と表現できるので、推定が楽になるというメリットがあります.
$R_0$: 基本再生産数の導入
$\beta$をconstantと仮定すると、$R_0 \equiv \beta/\gamma$という形で基本再生産数を定義できます. $R_0$はR nought, R zeroと読みます. なお、$\beta$がtime-varyingならば$R_0(t)$となるだけです.
$R_0$を用いて(2.1)~(2.4)を再定式化すると、
\[\begin{align*} \begin{split}\begin{aligned} \frac{d s}{d t} & = - \gamma \, R_0 \, s \, i \\ \frac{d e}{d t} & = \gamma \, R_0 \, s \, i - \sigma e \\ \frac{d i}{d t} & = \sigma e - \gamma i \\ \frac{d r}{d t} & = \gamma i \end{aligned}\end{split} \end{align*}\]ここで、各小文字$(s, e, i, r)$は人口$N$に対する各状態の割合を指します(例, $s\equiv S/N$).
Python Implementation
まずベースモデルとしてパラメーターが与えられた条件のもとでの、各状態割合の遷移をscipy.integrate.solve_ivpを用いて計算します. 手順としては
- 連立常微分方程式を定義
- scipy.integrate.solve_ivpを用いて遷移を計算
- 工程(2)の計算結果を可視化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
plt.style.use('ggplot')
## (1) 連立常微分方程式を定義
def F_base(x_array, t, gamma = 1/18, r_noght = 3.0, delta = 1/5.2):
s, e, i, r = x_array
## differential values
ds = - gamma * r_noght * s * i
de = gamma * r_noght * s * i - delta * e
di = delta * e - gamma * i
dr = gamma * i
return ds, de, di, dr
## (2) 遷移を計算
### 初期値の設定
D = 350
i_0 = 1e-7
e_0 = 4.0 * i_0
s_0 = 1 - i_0 - e_0
r_0 = 0.0
x_0 = np.array([s_0, e_0, i_0, r_0])
t = (0, D) # nearly 365 days
t_range = np.arange(0, D+1, 1)
### computation
sol = solve_ivp(F_base,
t_span=t,
y0=x_0,
method='RK45', # Tsitouras 5/4 Runge-Kutta Method
t_eval=t_range)
prob = sol.y
## (3.1) 計算結果を可視化
fig,ax = plt.subplots(figsize=(12,8))
ax.plot(prob.T,label = ['susceptible', 'exposed', 'infected', 'recovered'])
ax.legend()
ax.set_title('The SEIR Dynamics', fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('the segment ratio', fontsize=20);
## (3.2) Area plotで可視化
fig,ax = plt.subplots(figsize=(12,8))
ax.stackplot(t_range, prob, labels = ['susceptible', 'exposed', 'infected', 'recovered'])
ax.legend()
ax.set_title('The SEIR Dynamics', fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('the segment ratio', fontsize=20);


REMARKS
- 本件のようなnon-stiff differenrential equationsを用いる場合は、
Tsitouras 5/4 Runge-Kutta Methodを用いることが推奨 - scipy.integrate.odeintでも解けるが、scipy.integrate.solve_ivpの方が新しいコードを反映しているので推奨
3. モデルの拡張: $R_0$の水準に応じた死者と累積感染者数
死亡状態と累積感染者数の追加
累積感染者数の追加
累積感染者数(the cumulative caseload)を$C$とすると、各時点で$C = R + I$と計算できます. また、累積感染者はabsorbing stateなのでそのtime-derivativeは
\[\begin{align*} \frac{d}{dt}c(t) = \delta e \end{align*}\]死亡者数の追加
$D$を累積死者数, $d(t)= D/N$と定義したとき, その計算に必要なのは$\rho$死亡率の定義です. $D_0 = 0$と仮定し、the Infectedから退出した人数のうち$\rho$の割合で死ぬとすると、
\[\begin{align*} \frac{d}{dt}d(t) &= \rho \gamma i\\ \frac{d}{dt}r(t) &= (1 - \rho) \gamma i \end{align*}\]と元のベースモデルを変形します.
政策シミュレーション
Case 1: $R_0$の水準を政策で変更する
政策(Social distancingやワクチン普及)によって、外生的に $R_0$の水準をコントロールできた, $\bar R_0$とします. しかしその効果は瞬時には反映されずに
\[\frac{d}{dt}dR_0(t) = \eta(\bar R_0 - R_0(t)) \, \text{ where } \eta \in (0, 1)\]という遷移に従うとします.
Python simulation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
plt.style.use('ggplot')
## (1) 連立常微分方程式を定義
def F_extended(t, x_array, gamma, r_noght_target, delta, rho, eta):
s, e, i, r, c, d, r_noght = x_array
## differential values
ds = - gamma * r_noght * s * i
de = gamma * r_noght * s * i - delta * e
di = delta * e - gamma * i
dr_noght = eta * (r_noght_target - r_noght)
dr = (1 - rho) * gamma * i
dc = delta * e
dd = rho * gamma * i
return ds, de, di, dr, dc, dd, dr_noght
## (2) 遷移を計算
### policy target
r_0_target_array = np.linspace(1.6, 3.0, 6)
### Paramaters
gamma = 1/18
r_noght = 3.0
delta = 1/5.2
rho = 0.01
eta = 1/20
### 初期値の設定
i_0 = 1e-7
e_0 = 4.0 * i_0
s_0 = 1.0 - i_0 - e_0
r_0 = 0.0
c_0 = 0.0
d_0 = 0.0
x_0 = np.array([s_0, e_0, i_0, r_0, c_0, d_0, r_noght])
### 分析期間
D = 1000
t = (0, D) # nearly 365 days
t_range = np.arange(0, D+1, 1)
### computation
res = np.empty((6,7,D+1))
for array_index, r_0_target in enumerate(r_0_target_array):
sol = solve_ivp(F_extended,
t_span=t,
y0=x_0,
method='RK45',
t_eval=t_range,
args=[gamma, r_0_target, delta, rho, eta])
res[array_index,:,:] = sol.y
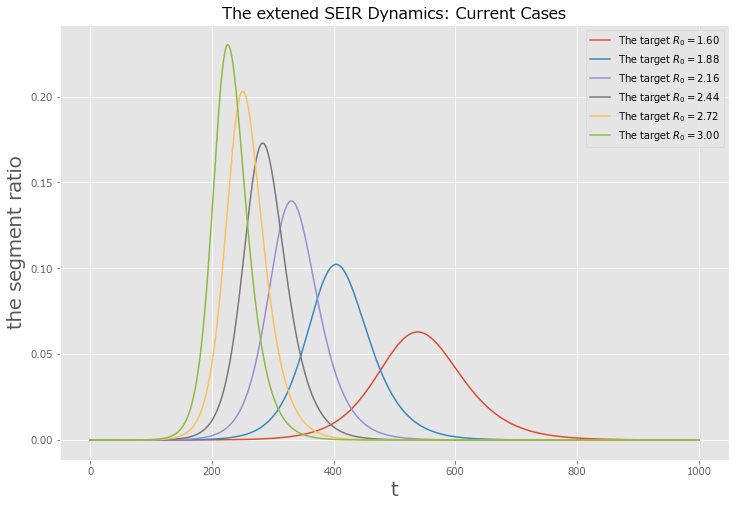
## (3) plot: The extened SEIR Dynamics, Current Cases
fig,ax = plt.subplots(figsize=(12,8))
label_list = ['The target $R_0 = {:.2f}$'.format(i) for i in r_0_target_array]
ax.plot(res[:,2,:].T,label = label_list)
ax.legend()
ax.set_title('The extened SEIR Dynamics: Current Cases', fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('the segment ratio', fontsize=20);
## (3) plot: The extened SEIR Dynamics, Cumulative infected
fig,ax = plt.subplots(figsize=(12,8))
label_list = ['The target $R_0 = {:.2f}$'.format(i) for i in r_0_target_array]
ax.plot(res[:,4,:].T,label = label_list)
ax.legend()
ax.set_title('The extened SEIR Dynamics: Cumulative infected ', fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('the segment ratio', fontsize=20);

REMARKS
- $R_0$がコントロールできる場合、発症者peakを抑えられ、病床資源制約の観点から有効な施策といえます
- また、トータルの累積感染者数を抑えて、COVID-19の収束も見込めると予想できます
- ただし、モデルによると収束までの期間は長くなるという結果も出てしまいます
Case 2: Lockdownの解除のタイミング
COVID-19本来のR noghtが$R_0 = 2.0$という条件のもと、t時点での新規感染者率が0.1%を上回った瞬間, $i > 0.001$, にLockdownを実施し、感染タッチポイントを8割削減することができるとします,i.e. $\bar\beta(t) = 0.2\beta(t)$. 一定期間経過後Lockdownを解除するとします.
この政府の施策の目的は(1)病床使用率の緩和, (2)累積死者数の削減の2つを目的としているとします.
また、過去の研究により、$R_0 = 2.0$というのはわかっており、およそ215日後には$i > 0.001$となることが予想されているとします.
Python simulation
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
def F_lockdown(t, x_array, gamma, r_noght_target, delta, rho, eta, target_period):
s, e, i, r, c, d, r_noght = x_array
## differential values
ds = - gamma * r_noght * s * i
de = gamma * r_noght * s * i - delta * e
di = delta * e - gamma * i
dr = (1 - rho) * gamma * i
dc = delta * e
dd = rho * gamma * i
if t > 220 and t < 220 + target_period:
dr_noght = eta * (r_noght_target - r_noght)
else:
dr_noght = eta * (2.0 - r_noght)
return ds, de, di, dr, dc, dd, dr_noght
## (2) 遷移を計算
### Paramaters
gamma = 1/18
r_noght = 2.0
delta = 1/5.2
rho = 0.01
eta = 1
### policy target
r_0_target = 0.2 * r_noght
target_period_array = [14, 30, 60, 90, 180]
### 初期値の設定
i_0 = 1e-7
e_0 = 4.0 * i_0
s_0 = 1.0 - i_0 - e_0
r_0 = 0.0
c_0 = 0.0
d_0 = 0.0
is_lockdown = 0
x_0 = np.array([s_0, e_0, i_0, r_0, c_0, d_0, r_noght])
### 分析期間
D = 1000
t = (0, D) # nearly 365 days
t_range = np.arange(0, D+1, 1)
### computation
res = np.empty((len(target_period_array),7,D+1))
for array_index, target_period in enumerate(target_period_array):
sol = solve_ivp(F_lockdown,
t_span=t,
y0=x_0,
method='RK45',
t_eval=t_range,
args=[gamma, r_0_target, delta, rho, eta, target_period])
res[array_index,:,:] = sol.y
## plot: The extened SEIR Dynamics, R_noght
fig,ax = plt.subplots(figsize=(12,8))
label_list = ['The lockdown period: {}'.format(i) for i in target_period_array]
ax.plot(res[:,5,:].T,label = label_list, lw=5, alpha=0.5)
ax.legend()
ax.set_title('The extened SEIR Dynamics: Cumulative death', fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('the segment ratio', fontsize=20);
## plot: The extened SEIR Dynamics, R_noght
fig,ax = plt.subplots(figsize=(12,8))
label_list = ['The lockdown period: {}'.format(i) for i in target_period_array]
ax.plot(res[:,2,:].T,label = label_list, lw=2, alpha=0.5)
ax.legend()
ax.set_title('The extened SEIR Dynamics: the current cases', fontsize=16)
ax.set_xlabel('t', fontsize=20)
ax.set_ylabel('the segment ratio', fontsize=20);

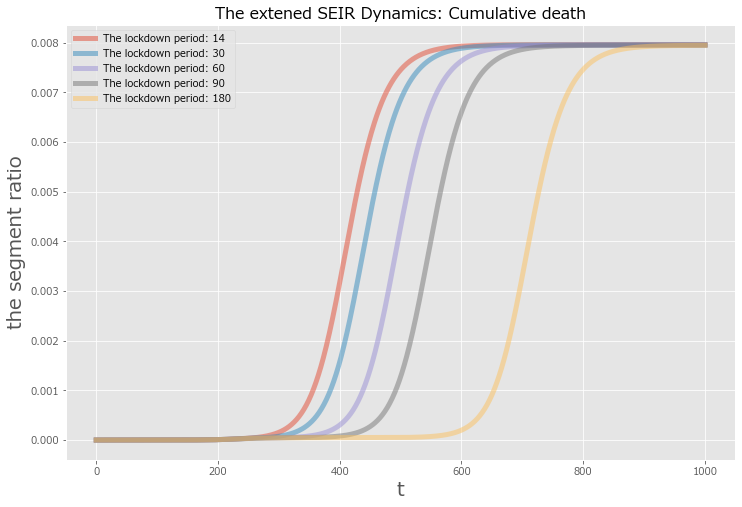
REMARKS
- Lockdownの期間が長いほど、新規感染者peakを未来にずらせることがわかります
- ただし、peakの感染者数及び最終的な累計死者数を減らす効果はなく、定常的に$R_0$や感染率を抑える施策を実施する必要は変わらないことがわかります
Ryo’s Tech Blog 関連記事
References
- 基礎から学ぶ 動学マクロ経済学に必要な数学, 中田真佐男著
- Quantitative Economics with Julia > Modeling COVID 19 with Differential Equations
- scipy.integrate.odeint
- scipy.integrate.solve_ivp
- Stiff Differential Equation
(注意:GitHub Accountが必要となります)