Table of Contents
1. 正弦関数の積の積分公式
$n,k$をそれぞれ自然数としたとき
\[\begin{align*} \int^{\pi}_0\sin nx \sin kx dx =\begin{cases} 0 & (k\neq n)\\[4pt] \frac{\pi}{2} & (k = n) \end{cases}\tag{A} \end{align*}\]正弦関数の積和公式
\[\sin \alpha\sin \beta=-\frac{1}{2} \left\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\right\} \tag{B}\]導出
余弦関数の加法定理より
\[\begin{align*} \cos(\alpha + \beta) &= \cos\alpha\cos\beta - \sin\alpha\sin\beta \tag{C}\\[4pt] \cos(\alpha - \beta) &= \cos\alpha\cos\beta + \sin\alpha\sin\beta\tag{D} \end{align*}\]$(C) - (D)$より
\[\cos(\alpha + \beta) - \cos(\alpha - \beta) = -2\sin\alpha\sin\beta\]従って,
\[\sin \alpha\sin \beta=-\frac{1}{2} \left\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\right\}\](導出終了)
正弦関数の積の積分公式の導出
正弦関数の積和公式 $(B)$ を用いて $(A)$を変形すると
\[\begin{align*} \int^{\pi}_0\sin nx \sin kx dx &= -\frac{1}{2}\int^{\pi}_0 \left\{\cos(n+k)x-\cos(n-k)x\right\} dx \\ &= -\frac{1}{2}\left\{\int^{\pi}_0\cos(n+k)x dx- \int^{\pi}_0\cos(n-k)xdx\right\} \tag{E} \end{align*}\]$n = k$ の場合
$n=k$の場合, $(E)$の第二項は
\[\int^{\pi}_0\cos 0 dx = \pi\]$(E)$の第一項は
\[\begin{align*} \int^{\pi}_0\cos(n+k)x dx &= -\left[\sin(n+k)x\right]^{\pi}_0\\ &= 0 \tag{F} \end{align*}\]従って,
\[\int^{\pi}_0\sin nx \sin kx dx = \frac{\pi}{2}\]\[-\left[\sin(n-k)x\right]^{\pi}_0\]$n \neq k$ の場合
は自明. 従って
\[\int^{\pi}_0\sin nx \sin kx dx = 0\](証明終了)
2. sinc関数の積分
sinc関数
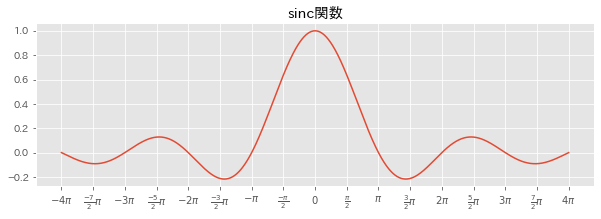
sinc関数の極限値について
$x\to\infty$の場合
$-1 \leq \sin x \leq 1$ より
\[-\frac{1}{x} \leq \frac{\sin x}{x} \leq \frac{1}{x}\]$x\to\infty$とすると両側から0で挟まれるので
\[\begin{align*} &0 \leq \lim_{x\to\infty}\frac{\sin x}{x} \leq 0\\ &\Rightarrow \lim_{x\to\infty} \frac{\sin x}{x} = 0 \end{align*}\](証明終了)
$x\to 0$の場合: Proof of sketch
三角形の面積の関係式より
\[\cos x < \frac{\sin x}{x} < 1\]を導出し,
\[\frac{\sin x}{x} = \frac{\sin -x}{-x}\]上記の関係式を用いてはさみうちの定理から証明するパターンが有名です. 詳しくは 高校数学の美しい物語 > sinx/xについて覚えておくべき2つのこと を参照してください.
sinc関数の積分の極限値について
sinc関数を$(\infty, \infty)$の範囲で積分すると
\[\int^{\infty}_{-\infty}\frac{\sin x}{x}dx = \pi\]という関係が知られています.
\[f(t) = \int^\infty_0\exp(-tx)\frac{\sin x}{x}dx\]Proof
という関数を置き, 両辺を $t$ で微分します.
\[\begin{align*} f'(t) &= \int^\infty_0-x\exp(-tx)\frac{\sin x}{x}dx\\ &= \int^\infty_0 \exp(-tx)(-\sin x)dx\\ &= [\cos x \exp(-tx)]^{\infty}_0 + t \int^{\infty}_0\exp(-tx)\cos x dx\\ &= -1 + t[\sin x\exp(-tx)]^{\infty}_0 + t^2\int^{\infty}_0\exp(-tx)\sin x dx\\ &= -1 - t^2\int^\infty_0 \exp(-tx)(-\sin x)dx\\ &= -1 - t^2f'(t) \tag{G} \end{align*}\]従って,
\[-f'(t) = \frac{1}{1+t^2}\]両辺を $t$ について$(0, \infty)$区間で積分すると, $\lim_{t\to\infty}f(t)=0$より
\[\begin{align*} LHS &= \int^\infty_0 f'(t)dt = -[f(t)]^{\infty}_0 = f(0)\\ RHS &= \int^\infty_0 \frac{1}{1+t^2} dt = [\tan^{-1}t]^{\infty}_0 = \frac{\pi}{2} \end{align*}\]なお, $\tan^{-1}t$の導出は $\arctan$の微分を用いています. sinc関数は偶関数だから, 従って,
\[\begin{align*} \int^\infty_0\exp(-tx)\frac{\sin x}{x}dx &= \frac{\pi}{2}\\ \int^\infty_{-\infty}\exp(-tx)\frac{\sin x}{x}dx &= \pi \end{align*}\](証明終了)
sinc関数を$(0, x)$の範囲で積分した計算結果をy軸に表示すると収束していくことがわかる

Appendix: 積和公式
\(\begin{align*} \cos x \cos y &= \frac{1}{2} \left\{\cos (x + y) + \cos(x - y)\right\}\\ \sin x \sin y &= -\frac{1}{2} \left\{\cos (x + y) - \cos(x - y)\right\}\\ \sin x \cos y &= \frac{1}{2} \left\{\sin (x + y) + \sin(x - y)\right\}\\ \cos x \sin y &= \frac{1}{2} \left\{\sin (x + y) - \sin(x - y)\right\} \end{align*}\)
Tips
偶関数と奇関数という関数の性質に着目すると覚えやすい
- 偶関数と偶関数の積は偶関数
- 奇関数と奇関数の積は偶関数
- 偶関数と奇関数の積は奇関数
Appendix:正弦関数の連続性
定義: 関数が区間 $I$ で連続
区間 $I$ で定義される関数 $f(x)$ が区間 $I$ で連続であるとは
$\forall \epsilon >0$, $\forall a \in I$, $\exists \delta(\epsilon, a) > 0$
\[\forall x \in I [|x-a|<\delta(\epsilon, a) \Rightarrow |f(x)-f(a)|<\epsilon ]\]正弦関数の和積公式
\[\begin{align*} \sin \alpha + \sin \beta &= 2\sin\frac{\alpha + \beta}{2} \cos\frac{\alpha - \beta}{2}\\ \sin \alpha − \sin \beta &= 2\cos\frac{\alpha + \beta}{2} \sin\frac{\alpha - \beta}{2} \end{align*}\]正弦関数の連続性の証明
$\mathbb R$上で定義される正弦関数について考える. 正弦関数の和積の公式と $|\cos x| \leq 1$, $|\sin x| \leq |x|$ より
\[\begin{align*} \lvert\sin x - \sin a\rvert &= \left\| 2\cos\frac{x + c}{2}\sin\frac{x - c}{2}\right\| \\ &\leq \left\|2 \cdot 1 \cdot \frac{x - c}{2}\right\|\\ &= \lvert x - c \rvert \end{align*}\]任意の$\epsilon >0$に対して, $\delta(\epsilon, a)=\epsilon$と定めると,
\[\forall x\in \mathbb R, \forall a \in \mathbb R [|x - a|<\epsilon\Rightarrow |\sin x - \sin a| < \epsilon]\]従って, 正弦関数は$\mathbb R$で(一様)連続である.
(証明終了)
References
書籍
オンラインマテリアル
(注意:GitHub Accountが必要となります)