Table of Contents
エアコンの仕組み
エアコンによる室温調整
物質が相変化するときに起こる「吸熱現象」と「発熱現象」を用いて, エアコンは温度のコントロールをしている
下の図のようにRA(ルームエアコン)は, 室外機と室内機が行きと帰りの2本のパイプでつながっています. これらパイプの内部には「冷媒」と呼ばれる流体が注入されており, この冷媒が室外機と室内機を循環しながら, 「相変化」(液体→気体→液体)することにより, エアコンとしての機能(=温度のコントロール)を実現しています.

冷媒の巡回を担当しているのがヒートポンプです. 熱機関では高温の熱源から低温の熱源に向かってエネルギーの移動が起こりますが, 低温の熱源から高温の熱源に向かってエネルギーを移動を実現する機構がヒートポンプとなります.
ヒートポンプは空気中の熱をポンプのように汲み上げて必要な場所に「移動させる」技術のことです. ヒートポンプを実現させる機器として圧縮機, 膨張弁, 熱交換器があります.
エアコンによるエネルギーの巡回
エアコンの主要コンポーネント
| 圧縮機 | 圧縮機は冷媒を圧縮高温にし巡回させる機器 振動や騒音が著しいので室外機の中にある エアコンの消費電力の8割を占める |
| 凝縮器 | 気体となった冷媒が液体に変化することで, 熱を放出する機器 |
| 膨張弁 | 冷媒を狭い隙間に通すことで低温低圧にする機器 室外機の中にある |
| 蒸発器 | 液体となった冷媒が気体に変化することで, 熱を吸収する機器 |
- 膨張弁で減圧された冷媒は蒸発器で相対的に温度の高い空気により蒸発(液相→気相)
- 圧縮機で高圧にされ, 凝縮器で相対的に温度の低い空気により凝縮する(気相→液相)
- 蒸発器では気化熱による吸熱, 凝縮器では凝縮熱による排熱
エアコンはこの仕組みをつかって, 暖房/冷房といった運転モードに合わせて室温をコントロールしています. 排熱と吸熱は室内機/室内機の内部にある熱交換器(内熱交と外熱交)を介して行われています.

ヒートポンプの効率性: COP, Coefficient Of Performance
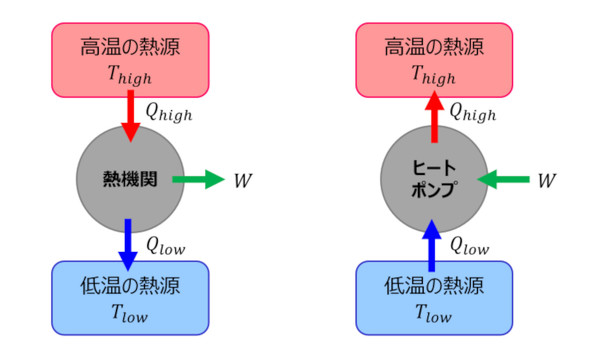
ヒートポンプは低温の熱源から$Q_{low}$のエネルギーを吸収し, 外部から$W$の仕事を受けてヒートポンプが作動し, $Q_{high}$の熱源を高温側に排出します. このとき, 以下の等式が成り立ちます
\[W = |Q_{high}| - |Q_{low}|\]ヒートポンプの効率はCOPという指標で表されます.
\[\begin{align*} COP = \frac{|Q_{high}|}{W} & \ \ \text{ where 暖房時}\\ COP = \frac{|Q_{low}|}{W} & \ \ \text{ where 冷房時} \end{align*}\]Column: ワットとジュールの関係
- ジュール, $J$: エネルギーそのものの大きさ
- ワット, $W$: 1秒間毎に発生・消費するエネルギーの大きさ, $J/s$と同じ
冷暖房能力
所定の時間で部屋の温度が所定の温度になるために必要な冷暖房能力を$A$とすると以下の形で表現できる
まず, 部屋の各辺から対象となる体積 $V_r$について
\[\begin{align*} V_r = \text{length}_r \times \text{width}_r \times \text{height}_r [m^3] \end{align*}\]ここで, 時間 $d [min]$ あたりで部屋の空気を維持準させるために必要な秒単位風量 $f_r$は
\[f_r = \frac{V_r}{60\times d} [m^3/s]\]時間 $d [min]$で温調到達するエアコンに求められる冷暖房能力を$A [W]$は
\[A = f_r \times \rho \times c_p \times \Delta T\]- $\rho$: 空気密度$kg/m^3$
- $c_p$: 空気比熱$J/kg\cdot K$
- $\Delta T$: 変化させたい温度差 $[K]$
冷暖房能力から必要冷媒質量流量の導出
冷暖房に必要な比エンタルピーを$\Delta h [J/kg]$, 必要な冷媒質量流量を$G[kg/s]$とすると,
\[A = \Delta h \times G\]エンタルピーとは空気が持つ熱量のことで単位質量あたりのエンタルピーを比エンタルピーといいます. 比エンタルピーは冷媒の種類のよって固定されるので, 必要冷媒質量流量$G$は冷暖房能力がわかれば導出することができます.
Def: エンタルピー
\[H = U + P \times V\]- H: エンタルピー
- U: 内部エネルギー $[J]$
- P: 圧力 $[Pa]$
- V: 体積 $m^3$
圧縮機の仕様: $W$の導出
圧縮機を通過する流量 $v [m^3/s]$は, 通過するガスの比容積 $\gamma [m^3/kg]$, 圧縮機の吸い込み容積 $V_c [m^3]$, 圧縮機の回転周期 $T_c [s]$より
\[\begin{align*} v &= G \times \gamma\\ v &= \frac{V_c}{T_c} \end{align*}\]以上より, 冷暖房能力から必要な圧縮機の吸い込み容積/回転数比率が導出される. 次にここから $W$ の導出をする
凝縮器と蒸発器に対応する低圧側温度 $p_{low}$と高圧側温度 $p_{high}$とすると $W$ は次のように表される
\[W \propto V_c \times (p_{high} - p_{low})\]Appendix: 冷媒R410Aの物性値
| 温度 ℃ |
蒸気圧 Pa |
液相密度 $kg/m^3$ |
液相定圧比熱 $J/kg\cdot K$ |
気化熱 $J/kg$ |
気相密度 $kg/m^3$ |
気相定圧密度 $J/kg\cdot K$ |
|---|---|---|---|---|---|---|
| $-20$ | $1.088\times 10^6$ | $1128$ | $1.579\times 10^3$ | $2.132\times10^5$ | $41.18$ | $1.246\times10^3$ |
| $0$ | $1.889\times 10^6$ | $1033$ | $1.679\times 10^3$ | $1.820\times10^5$ | $75.31$ | $1.561\times10^3$ |
| $20$ | $3.071\times 10^6$ | $906.8$ | $2.256\times 10^3$ | $1.389\times10^5$ | $139.2$ | $2.415\times10^3$ |
| $40$ | $4.765\times 10^6$ | $620.5$ | $2.452\times 10^3$ | $4.548\times10^4$ | $343.2$ | $2.751\times10^4$ |
References
(注意:GitHub Accountが必要となります)