18世紀までの関数論とテイラー展開

関数

Def: 関数

\(X \subset \mathbb R^n, Y\subset \mathbb R^n\) とする．\(X\) から \(Y\) への関数（実関数）とは，\(X\) の任意の元 \(x\) に対して，\(Y\) の１つの元を対応させる規則をいう． このような \(X\) から \(Y\) への関数を

\[ f: X\to Y \]

を記述し，集合 \(X\) を関数 \(f\) の定義域(domain)，\(Y\) を値域(range) という．

\(y = x^2\) としたとき，\(y\) は区間 \((-\infty, \infty)\) における \(x\) の関数と呼ばれます．関数の例としては以下，

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-1, 1, 100)

plt.plot(x, x**2)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()

plt.plot(x , np.sqrt(1 - x**2))
plt.gca().set_aspect('equal', adjustable='box')
plt.show()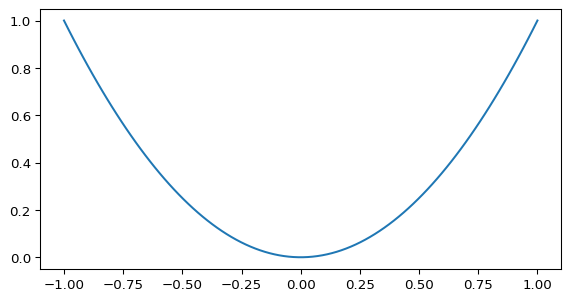

\(y = x^2\)

\(y = \sqrt{1 - x^2}\)

▶  古典的な関数

歴史的に関数はまず，

• 四則演算で表される代数式（\(x^2 + 2x +1\), \(x + \frac{1}{x}\), \(x + \sqrt{4x^2 + 1}\)）
• 独立変数の代数式で表せない超越関数（\(a^x, \log x, \sin x, \arctan x\)）

に限られていました．これら関数は，各点周りでテイラー展開ができるという特徴があります．

平均値の定理からTaylorの公式へ

Theorem 1 : 平均値の定理

区間 \([a, b]\) において，\(f(x), g(x)\) は連続で, \((a, b)\) において微分可能とする．このとき，ある点 \(\xi \in (a, b)\) において，

\[ \frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f^\prime(\xi)}{g^\prime(\xi)}\label{eq-mean-value} \]

ただし，\(g(a)\neq g(b)\)．\(f^\prime(x), g^\prime(x)\) は区間内で同時に \(0\) にならないと仮定する．

Proof

\(F(x) - \mu f(x) - \lambda g(x)\) とおき，\(F(a) = F(b) = k\) となるように適当に \(\lambda:\mu\) を定める．

このとき，

\[ \begin{gather} \mu f(a) - \lambda g(a) = \mu f(b) - \lambda g(b)\\ \Rightarrow \mu (f(b) - f(a)) = \lambda (g(b) - g(a))\\ \Rightarrow \mu (f(b) - f(a)) = \lambda (g(b) - g(a))\\ \Rightarrow \mu = g(b) - g(a), \lambda = f(b) - f(a) \end{gather} \]

として，

\[ F(x) = \{g(b)-g(a)\}f(x) - \{f(b)-f(a)\}g(x) \]

ここで，\(G(x) = F(x) - k\) を考える．有界閉区間 \([a, b]\) において \(f(x), g(x)\) は連続であるので，有界閉区間 \([a, b]\) において \(F(x)\) および \(G(x)\) も連続関数である．関数の連続性より， とある \(\xi \in [a, b]\) で \(G(x)\) は最大値 \(G(\xi) = M < \infty\) をとる．

\(M > 0\) のとき，

\(x = \xi\) において \(\Delta G \leq 0\). 故に

• \(\Delta x > 0\) とすれば \(\displaystyle\frac{\Delta G}{\Delta x} \leq 0\), 従って，\(G^\prime(\xi)\leq 0\)
• \(\Delta x < 0\) とすれば \(\displaystyle\frac{\Delta G}{\Delta x} \geq 0\), 従って，\(G^\prime(\xi)\geq 0\)

従って，\(G^\prime(\xi) = 0\). \(M = 0\) のときは，同様に最小値 \(G(\xi) = M > -\infty\) を考えると \(G^\prime(\xi)\geq 0\) を得る．最小値と最大値が \(0\) の場合は \(G(x)\) が常に \(0\) であるので，\(x \in (a, b)\) において \(G^\prime(x) = 0\) は自明．

このとき，\(F(x) - k = G(x)\) より

\[ \begin{align} F^\prime(\xi) = \{g(b)-g(a)\}f^\prime(\xi) - \{f(b)-f(a)\}g^\prime(\xi) = 0 \end{align} \]

よって，

\[ \frac{f(b) - f(a)}{g(b) - g(a)} = \frac{f^\prime(\xi)}{g^\prime(\xi)} \]

が成立する．

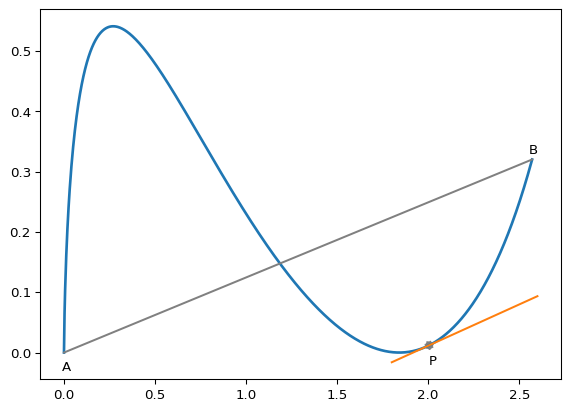
平均値の定理を幾何学的に考察してみます．独立変数 \(t\) について，曲線

\[ x = f(t), y=g(t)\qquad t \in [a. b] \]

を考えます．このとき，\(t=a, t=b\) に対応する \((x, y)\) をそれぞれ \(A, B\) とすると，\(\eqref{eq-mean-value}\) のLHSが弦ABの勾配に対応します． このとき，\(x = f(t), y=g(t)\) の曲線上のとある点 \(P: t= \xi\) の接線が弦ABの勾配と平行になることを定理は示しています．\(f^\prime(x), g^\prime(x)\) は区間内で同時に \(0\) にならないと仮定は，曲線が各点において 確定の接線を有することを意味します．

def func_x(x):
    return np.sin(x) + x

def func_y(x):
    return x * np.log(x) ** 2

def tangent(x, x_0):
    return func_y(x_0) + (x- func_x(x_0)) * (np.log(np.pi/2) ** 2.5)


t = np.linspace(1e-18, np.pi/2, 1000)
t2 = np.linspace(1.8, 2.6, 100)
x, y = func_x(t), func_y(t)
t_0 = 1.11

# plot
plt.plot(x, y, linewidth=2)

# # add line
plt.plot([0, func_x(np.pi/2)], [0, func_y(np.pi/2)], color="gray")
plt.text(-0.01, -0.03, "A")
plt.text(2.55, 0.33, "B")

# # add tangent
# plt.text(x_0, sample_func(x_0)+1e-4, "P: x = $\exp(-2)$")
plt.scatter(func_x(t_0), func_y(t_0), color="gray", linestyle="dotted")
plt.text(func_x(t_0), -0.02, "P")
plt.plot(t2, tangent(t2, t_0))

plt.show()

Figure 1: \(t\in [0,\pi/2]\) 区間で定義された \(x = \sin(t) +t, y = \begin{cases}t(\log(t))^2 & (t\in(0, \pi/2))\\0 & t = 0\end{cases}\)

🍵 Green Tea Break

実数空間 \(\mathbb R\) の部分集合 \(I\) で定義された関数 \(f(x)\) が区間 \(I\) の点 \(a\) において連続であるとは

\[ \lim_{x\to a}f(x) = f(a) \]

が成り立つことをいいます．

\[ f(t) = \begin{cases}t(\log(t))^2 & (t\in(0, \pi/2))\\0 & t = 0\end{cases} \]

はロピタルの定理を用いると，

\[ \begin{align} \lim_{t\to 0} t(\log(t))^2 &= \lim_{t\to 0} \frac{(\log(t))^2}{t^{-1}}\\ &= \lim_{t\to 0} \frac{2(\log(t))\frac{1}{t}}{-t^{-2}}\\ &= \lim_{t\to 0} \frac{2(\log(t))}{-t^{-1}}\\ &= \lim_{t\to 0} \frac{2t^{-1}}{t^{-2}}\\ &= \lim_{t\to 0} 2t = 0 \end{align} \]

以上のように連続性を示すことが出来ます．

Taylorの公式

Theorem 2

ある区間において．\(f(x)\) は第 \(n\) 階まで微分可能とする．このときその区間において，\(a\) は定点，\(x\) を任意の点とするとき

\[ \begin{gather} f(x) = f(a) + \frac{f^\prime(a)}{1!}(x-a) + \frac{f^{\prime\prime}(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n-1)}(a)}{(n-1)!}(x-a)^{n-1} + \frac{f^{(n)}(\xi)}{(n)!}(x-a)^{n}\label{eq-taylor}\\ \text{s.t } \quad \xi = a + \theta(x-a), \qquad 0 <\theta<1 \end{gather} \]

\(\frac{f^{(n)}(\xi)}{(n)!}(x-a)^{n}\) は \(R_n\) と表されることもあり，剰余項とよびます．

Proof

\[ F(x) = f(x) - \{f(a) + \frac{f^\prime(a)}{1!}(x-a) + \frac{f^{\prime\prime}(a)}{2!}(x-a)^2 + \cdots + \frac{f^{(n-1)}(a)}{(n-1)!}(x-a)^{n-1}\}\label{eq-residual} \]

とおく．このとき，定義より

\[ F(a) = F^{\prime}(a) = F^{\prime\prime}(a) = \cdots = F^{n-1}(a) = 0 \]

ここで，

\[ G(x) = (x - a)^n \]

と定義すると第 \(n\) 階まで微分可能であり，また \(G(a) = 0\)．このとき，中間値の定理より

\[ \begin{align} \frac{F(x) - F(a)}{G(x) - G(a)} &= \frac{F(x)}{G(x)}\\ &= \frac{F(x)}{(x-a)^n}\\ &= \frac{F^\prime(x_1)}{n(x_1-a)^{n-1}} \qquad x_1 \in (a, x) \end{align} \]

同様に

\[ \frac{F^\prime(x_1)}{n(x_1-a)^{n-1}} = \frac{F^{\prime\prime}(x_2)}{n(n-1)(x_2-a)^{n-2}} \qquad x_2 \in (a, x_1) \]

\(f(x)\) は第 \(n\) 階まで微分可能であるので，\(F(x)\) も第 \(n\) 階まで微分可能．従って，

\[ \frac{F(x)}{(x-1)^n} = \frac{F^{n}(\xi)}{n!} \qquad \exists\xi \in (a, x) \]

つまり

\[ F(x) = \frac{F^{n}(\xi)}{n!}(x-a)^n \]

これを \(\eqref{eq-residual}\) に代入して整理すると \(\eqref{eq-taylor}\) を得る．

整式はそれ自身が有限個の項で完結したテイラー展開のしていますし，無限等比級数の公式

\[ \frac{1}{1 + r} = 1 - r + r^2 - r^3 + \cdots = \sum_{i=0}(-r)^i \qquad (-1 < r < 1) \]

は \(x = 1\) 周りでの関数 \(f(x) = 1/ x\) のテイラー展開となっており，\(x = 1 + r\) とすると

\[ \begin{align} \frac{1}{1+r} &= 1 + \frac{(-1)}{1!}r + \frac{(-1)\times(-2)}{2!}r^2 + \frac{(-1)\times(-2)\times(-3)}{3!}r^3 + \cdots\\ &= 1 - r + r^2 - r^3 + \cdots \end{align} \]

と確認することが出来ます．三角関数も

\[ \begin{align} \cos x &= 1 - \frac{1}{2}x^2 + \frac{1}{24}x^4 - \cdots\\ \sin x &= x - \frac{1}{6}x^3 + \frac{1}{120}x^5 - \cdots \end{align} \]

とテイラー展開することが出来ます．そのため，18世紀までの数学界では，関数は各点周りで冪級数にテイラー展開できるので，微分や積分もテイラー展開を応用して形式的な代数的計算で十分と考えられてました． 19世紀になると任意の関数 \(f(x)\) は

\[ f(x) \sim \frac{a_0}{2} + \sum_{n=1}^\infty(a_n\cos nx + b_n \sin nx) \]

で表すことができるのではないか？という主張が登場し，関数，微分，積分の理論の見直しの必要性が認識されるようになりました．

Example 1 : テイラー展開の例

次の関数の点 \(a\) のまわりのテイラー展開を剰余項を含めて \(h^3\) まで書き下すと以下のようになります

\[ \begin{align} \log(a+h) &= \log(a) + \frac{h}{a} - \frac{1}{2}\frac{h^2}{a^2} + \frac{1}{3}\frac{h^3}{(a+\theta h)^3}\\ (a+h)^\beta &= a^\beta + \beta a^{\beta-1}h + \frac{\beta(\beta-1)}{2!}a^{\beta-2}h^2+ \frac{\beta(\beta-1)(\beta-2)}{3!}(a+\theta h)^{\beta-3}h^3 \end{align} \]

ただし，\(0 < \theta < 1\) とします．

Taylor展開の応用: \(e\) が無理数であることの証明

\(f(x) = \exp(x)\) を マクローリン展開すると

\[ \exp(x) = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots + \frac{x^n}{n!} + R_{n+1} \]

\(x = 1\) としたとき，

\[ e = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \cdots + \frac{1}{n!} + R_{n+1} \]

剰余項 \(R_{n+1}0\) は

\[ R_{n+1} = \frac{\exp(\theta)}{(n+1)!} > 0 \quad \exists\theta \in (0, 1) \]

つまり，

\[ R_{n+1} = \frac{\exp(\theta)}{(n+1)!} < \frac{3}{(n+1)!} \]

ここで，\(e\) を有理数として \(e = m/n\) と既約分数で表せると仮定する．このとき，\(n!e\) は仮定より整数となるので

\[ 1 \leq n!R_{n+1} = \frac{\exp(\theta)}{n+1} < \frac{3}{n+1} \]

従って，\(n+1 <3\) つまり \(n < 2\)，従って，\(n = 1\) を得る．このとき，\(m\) は整数なので \(e = m\) となるが \(2 < e < 3\) より矛盾．従って，\(e\) は無理数となる．