関数の連続性

解析
Author

Ryo Nakagami

Published

2025-02-03

連続関数

変数 \(x\) が限りなく \(a\) に近づくとき，\(f(x)\) も \(f(a)\) に近づくならば，\(f(x)\) は \(x=a\) において連続である，といいます．つまり，

\[ x\to a \text{ ならば } f(x) \to f(a) \]

Def: \(\epsilon\)-\(\delta\) 論法的連続性

任意の \(\epsilon >0\) に対して，ある \(\delta > 0\) が存在して，

\[ \vert x - a \vert < \delta \Rightarrow \vert f(x) - f(a)\vert < \epsilon \]

を満たすとき，\(x=a\) において \(f(x)\) は連続であるという．

Example 1

\(f(x) = \sqrt{x}\) について，\(a > 0\) で連続であることを以下示します．

\[ \begin{align} \vert \sqrt{x} - \sqrt{a} \vert &= \left\vert\frac{(\sqrt{x} - \sqrt{a})(\sqrt{x} + \sqrt{a})}{\sqrt{x}+\sqrt{a}}\right\vert\\ &= \left\vert\frac{x - a}{\sqrt{x}+\sqrt{a}}\right\vert\\ &\leq \left\vert\frac{x - a}{\sqrt{a}}\right\vert \end{align} \]

ここで，\(\vert x - a\vert < \delta(\epsilon) = \epsilon\sqrt{a}\) と定めると

\[ \vert x - a\vert < \delta(\epsilon) \Rightarrow \vert \sqrt{x} - \sqrt{a}\vert < \epsilon \]

Example 2 : 三角関数の連続性

\(x = a + h\) とおくと，和積の公式を用いて

\[ \begin{align} \vert \sin(x) - \sin(a) \vert &= 2\left\vert \cos\frac{x+a}{2}\sin\frac{x-a}{2} \right\vert\\ &= 2\left\vert \cos\left(a + \frac{h}{2}\right)\sin\frac{h}{2} \right\vert\\ &\leq 2\left\vert\frac{h}{2}\right\vert \cdot 1\\ &=\vert h \vert \end{align} \]

\(\cos x = \sin\left(x + \frac{\pi}{2}\right)\) であるので，\(\sin x\) が連続であるならば, \(\cos x\) も連続．

Theorem 1 : 連続関数の定数倍

\(f(x)\) は \(x=a\) で連続であるとします．このとき，定数 \(c\) を用いた \(cf(x)\) も \(x=a\) にて連続となります．

Proof

仮定より

\[ \forall \eta > 0, \exists \delta(\eta) > 0, \vert x - a\vert < \delta(\eta)\Rightarrow\vert f(x) - f(a)\vert < \eta \]

このとき，任意の \(\epsilon > 0\) に対して，

\[ \eta = \frac{\epsilon}{\vert c \vert} >0 \]

と対応させると，

\[ \forall \epsilon > 0, \exists \delta(\epsilon) > 0, \vert x - a\vert < \delta(\epsilon)\Rightarrow\vert f(x) - f(a)\vert < \frac{\epsilon}{\vert c \vert } \]

つまり，

\[ \forall \epsilon > 0, \exists \delta(\epsilon) > 0, \vert x - a\vert < \delta(\epsilon)\Rightarrow \vert c\vert\vert f(x) - f(a)\vert < \epsilon \]

これを変形すると

\[ \forall \epsilon > 0, \exists \delta(\epsilon) > 0, \vert x - a\vert < \delta(\epsilon)\Rightarrow \vert cf(x) - cf(a)\vert < \epsilon \]

Theorem 2 : 連続関数の和


\(f(x), g(x)\) は \(x=a\) で連続であるとします．このとき，\(f(x) + g(x)\) も \(x=a\) にて連続となります．

Proof

仮定より

\[ \begin{align} \vert x - a \vert < \delta&\Rightarrow \vert f(x) - f(a)\vert < \epsilon/2\\ \vert x - a \vert < \eta&\Rightarrow \vert g(x) - g(a)\vert < \epsilon/2 \end{align} \]

ここで，\(M = \min(\delta, \eta)\) とすると，

\[ \begin{align} \vert x - a \vert < M&\Rightarrow \vert f(x) - f(a)\vert < \epsilon/2\\ \vert x - a \vert < M&\Rightarrow \vert g(x) - g(a)\vert < \epsilon/2 \end{align} \]

また

\[ \begin{align} \vert(f(x) - g(x)) - (f(a) + g(a)) &= \vert(f(x) - f(a)) + (g(x) + g(a))\vert\\ &\leq \vert(f(x) - f(a))\vert + \vert (g(x) + g(a))\vert \end{align} \]

従って，\(\vert x - a \vert < M\) であるならば

\[ \begin{align} \vert (g(x) + f(x)) - (g(a) + f(a))\vert \leq \vert(f(x) - f(a))\vert + \vert (g(x) + g(a))\vert < \epsilon \end{align} \]

Theorem 3 : 連続関数の線型結合

\(f(x), g(x)\) は \(x=a\) で連続であるとします．このとき，定数 \(c_1, c_2\)に対して \(c_1f(x) + c_2g(x)\) も \(x=a\) にて連続となります．

Proof

\[ \begin{align} \vert x - a \vert < \delta&\Rightarrow \vert f(x) - f(a)\vert < \frac{\epsilon}{2\vert c_1\vert}\\ \vert x - a \vert < \eta&\Rightarrow \vert g(x) - g(a)\vert < \frac{\epsilon}{2\vert c_2\vert} \end{align} \]

として，\(M = \min(\delta, \eta)\) とすれば，上記と同様に連続性を示すことができます．

Theorem 4 : 連続関数の積

\(f(x), g(x)\) は \(x=a\) で連続であるとします．このとき，\(f(x)g(x)\) も \(x=a\) にて連続となります．

Proof

\[ \vert x - a \vert < \delta(1) \Rightarrow \vert f(x) - f(a)\vert < 1 \]

とすると，

\[ \vert x - a \vert < \delta(1) \Rightarrow \vert f(x) \vert < 1 + \vert f(a) \vert \]

\(\delta, \eta\) を以下のように定め，

\[ \begin{align} \vert x - a \vert < \delta &\Rightarrow \vert f(x) - f(a)\vert < \frac{\epsilon}{2(1 + \vert f(a) \vert + \vert g(a) \vert)}\\ \vert x - a \vert < \eta &\Rightarrow \vert g(x) - g(a)\vert < \frac{\epsilon}{2(1 + \vert f(a) \vert + \vert g(a) \vert)} \end{align} \]

\[ \delta(\epsilon) = \min (\delta(1), \delta, \eta) \]

とすると，

\[ \begin{align} \vert x - a \vert < \delta(\epsilon) \Rightarrow &\vert f(x)g(x) - f(a)g(a)\vert\\[5pt] &= \vert f(x)(g(x) - g(a)) + g(a)(f(x) - f(a))\vert\\[5pt] &\leq \vert f(x)\vert \vert(g(x) - g(a))\vert + \vert g(a)\vert\vert(f(x) - f(a))\vert\\[5pt] &< (1 + \vert f(a) \vert)\frac{\epsilon}{2(1 + \vert f(a) \vert + \vert g(a) \vert)} + \vert g(a)\vert \frac{\epsilon}{2(1 + \vert f(a) \vert + \vert g(a) \vert)}\\ &= \epsilon \end{align} \]

よって，連続性が示された．

Theorem 5 連続関数の逆数

\(f(x)\) は \(x=a\) で連続であるとします．このとき，\(f(a)\neq 0\) であるならば \(1/f(x)\) も \(x=a\) にて連続となります．

Proof

連続性の仮定より

\[ \vert x - a \vert < \delta(\vert f(a)/2\vert) \Rightarrow \vert f(x) - f(a)\vert < \frac{\vert f(a)\vert}{2} \]

とすると，

\[ \vert x - a \vert < \delta(\vert f(a)/2\vert) \Rightarrow \frac{\vert f(a)\vert}{2} < \vert f(x)\vert \]

このとき，

\[ \begin{align} \left\vert \frac{1}{f(x)} - \frac{1}{f(a)} \right\vert &= \left\vert \frac{f(x) - f(a)}{f(x)f(a)} \right\vert\\ &< \left\vert \frac{f(x) - f(a)}{(f(a))^2 / 2} \right\vert \end{align} \]

従って，\(\vert x - a \vert < \eta \Rightarrow \vert f(x) - f(a)\vert < \displaystyle\frac{\epsilon\vert (f(a))^2\vert}{2}\) となるような \(\eta\) を用いて，

\[ \delta(\epsilon) = \min(\delta(\vert f(a)/2\vert), \eta) \]

とすれば

\[ \vert x - a \vert < \delta(\epsilon) \Rightarrow \left\vert \frac{1}{f(x)} - \frac{1}{f(a)} \right\vert < \epsilon \]

右連続と左連続

点 \(a\) における極限を考えるとき，

  • \(x\) が増大しつつ \(a\) に（左側から）近づく, \(\lim_{x\to a-0}\)
  • \(x\) が減少しつつ \(a\) に（右側から）近づく, \(\lim_{x\to a+0}\)

それぞれの場合を分けて取り扱うことがあります．

Example 3

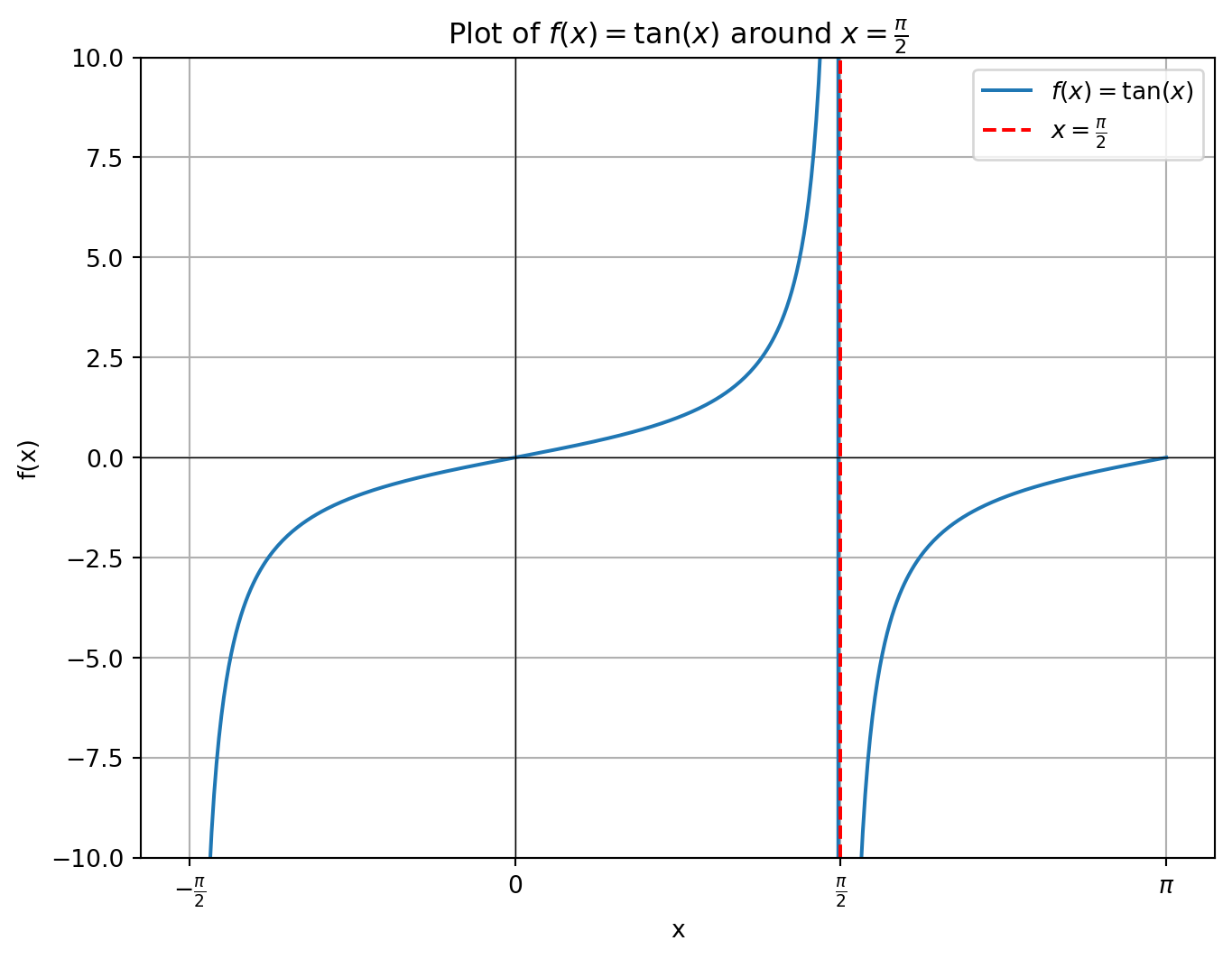
\(f(x) = \tan x\) について，\(x = \pi/2\) における極限を考えてみます．

Code 
import numpy as np
import matplotlib.pyplot as plt
import sympy as sy

x = sy.Symbol('x')
f = sy.tan(x)

x_vals = np.linspace(-np.pi/2+1e-6, np.pi, 400)
y_vals = np.tan(x_vals)

plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, label=r'$f(x) = \tan(x)$')
plt.ylim(-10, 10)
plt.xticks([-np.pi/2, 0, np.pi/2, np.pi], [r'$-\frac{\pi}{2}$', '0', r'$\frac{\pi}{2}$', r'$\pi$'])
plt.axvline(np.pi/2, color='r', linestyle='--', label=r'$x = \frac{\pi}{2}$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'Plot of $f(x) = \tan(x)$ around $x = \frac{\pi}{2}$')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend()
plt.grid(True)
plt.show()

Figure 1

上記の図のように，

\[ \begin{align} \lim_{x\to \pi/2+0} \tan x &= -\infty\\ \lim_{x\to \pi/2-0} \tan x &= \infty \end{align} \]

実際に，sympy で確認してみると

# DO NOT USE np.pi
print(f"左極限: {sy.limit(sy.tan(x), x, sy.pi/2, '-')}")
print(f"右極限: {sy.limit(sy.tan(x), x, sy.pi/2, '+')}")
左極限: oo
右極限: -oo

▶  右連続と左連続

\[ \begin{align} f(a) &= \alpha\\[5pt] \lim_{x\to a-0} f(x) &= \alpha\\ \lim_{x\to a+0} f(x) &= \beta \neq \alpha \end{align} \]

のとき，\(f(x)\) は \(x = a\) において左連続といいます．

\(f(x)\) が閉区間 \([a, b]\) において定義されているとき，

  • \(x=a\) においては右連続
  • \(x=b\) においては左連続

であることを意味します．開区間 \((a, b)\) において定義されているとき，\(f(a+0)\) が確定ならば，それを \(f(a)\) として定義域を \([a, b)\) 区間に拡張すると \(f(x)\) は \(x=a\) において右連続になります．

一方，\((0, \infty)\) 区間で定義された関数 \(\displaystyle f(x) = \frac{1}{x}\) は開区間では連続ですが，\(x = 0\) のときは定義されません．このとき，\(f(0) = 0\) として定義域を \([0, \infty)\) に拡張すると，\(x=0\) で連続な関数にはなりませんし，\(f(0)\) をどんな値にしたとしても，\(x=0\) の近傍において, \(f(x)\) はいくらでも大きくなってしまうので，連続な関数にはなりません．

📘 REMARKS

  • 開区間 \((a, b)\) で定義された連続な関数が，開区間 \([a, b]\) の連続な関数に拡張できるとは限らない

Example 4 : 右連続関数と累積分布関数

離散確率変数 \(X\sim\operatorname{Bin}(5, 1/3)\) を考えます．離散確率変数の累積分布関数 \(F(x)\) は

\[ F(x) = \operatorname{P}(X \leq x) = \sum_{y\leq x}p(y) \qquad p(y): \text{確率関数} \]

と定義されるので，\(F(x)\) は右側連続となります．実際に

Code 
import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import binom

n, p = 5, 1 / 3
x = np.arange(0, 6)
cdf = binom.cdf(x, n, p)

fig, ax = plt.subplots(1, 1)
ax.hlines(cdf, x, x + 1, color="gray")
ax.step(x, cdf, where="post", color="gray", linestyle="dotted")
ax.plot(x, cdf, "o", color="gray")
ax.scatter(x[:-1] + 1, cdf[:-1], marker="$\u25EF$", alpha=0.5, color="gray")
ax.set_xlabel("x")
ax.set_ylabel("F(x)")
ax.set_title("CDF of Binomial Distribution (n=5, p=1/3)")
plt.show()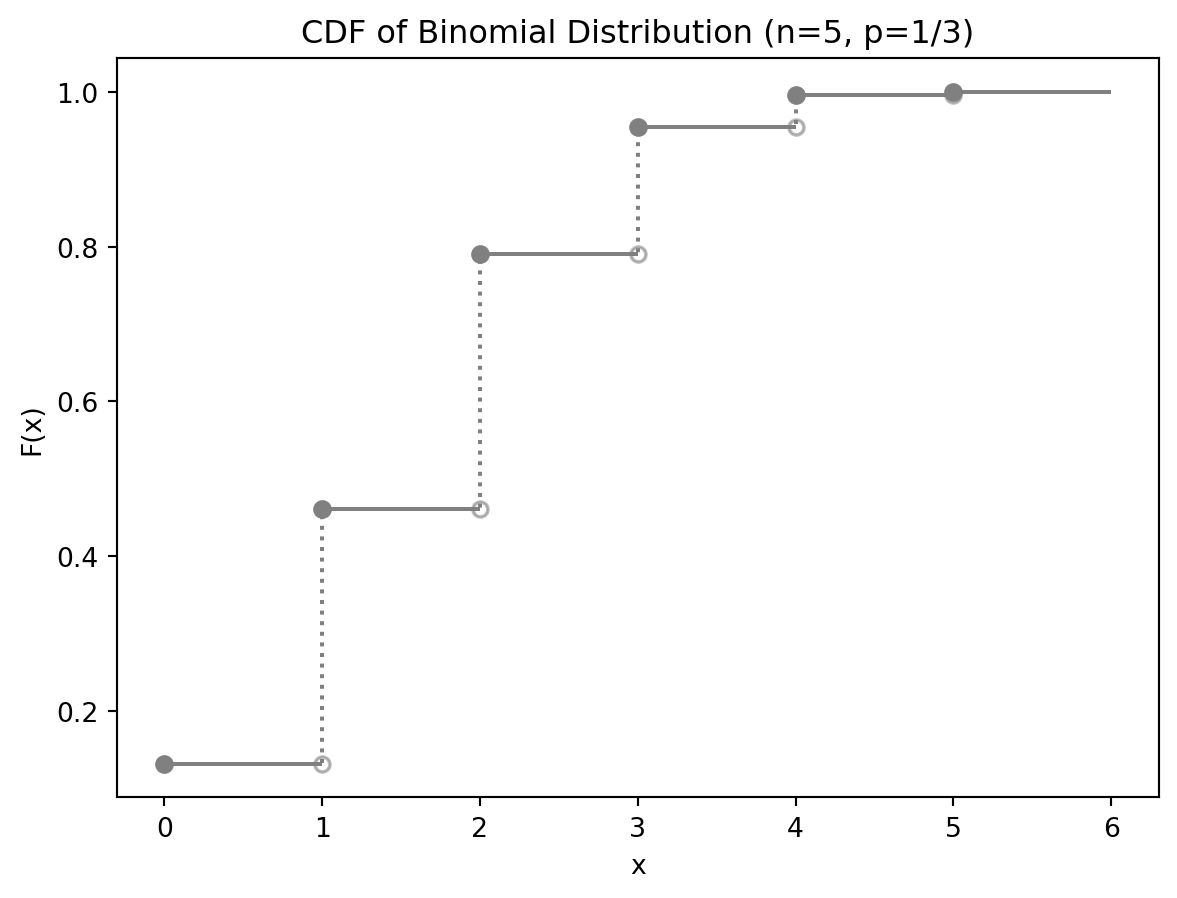

Figure 2

このとき，確率関数は

\[ p(x) = F(x) - \lim_{x_n\to x-0}F(x_n) \]

とすることで計算することが出来ます．一方，\(F(x) = \operatorname{P}(X < x)\) と定義すると左連続となります．

関数の拡張

\[ f(x) = \frac{\sin x}{x} \]

を考えます．この関数は \(x - 0\) で定義されていないですが

\[ \begin{align} f(x) = \left\{\begin{array}{c} \frac{\sin x}{x} & (x\neq 0)\\ 1 & (x = 0) \end{array}\right. \end{align} \]

と \(x = 0\) で連続かつ微分可能になるように拡張することが出来ます．この拡張された関数を特にsinc関数と呼びます．

Code 
import numpy as np
import matplotlib.pyplot as plt

# Define the sinc function
def sinc(x):
    return np.sinc(x / np.pi)

def inverse_x(x):
    return 1/x

# Generate x values
x_vals = np.linspace(-10*np.pi, 10*np.pi, 400)
y_vals = sinc(x_vals)

# Plot the sinc function
plt.figure(figsize=(8, 6))
plt.plot(x_vals, y_vals, label=r'$f(x) = \frac{\sin(x)}{x}$')
plt.plot(x_vals, inverse_x(x_vals), label=r'$f(x) = \frac{1}{x}$')
plt.xticks(np.arange(-10*np.pi, 11*np.pi, np.pi), 
           [r'$-10\pi$', r'$-9\pi$', r'$-8\pi$', r'$-7\pi$', r'$-6\pi$', r'$-5\pi$', r'$-4\pi$', r'$-3\pi$', r'$-2\pi$', r'$-\pi$', '0', r'$\pi$', r'$2\pi$', r'$3\pi$', r'$4\pi$', r'$5\pi$', r'$6\pi$', r'$7\pi$', r'$8\pi$', r'$9\pi$', r'$10\pi$'])
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'Plot of $f(x) = \frac{\sin(x)}{x}$')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.ylim(-1.1, 1.1)
plt.legend()
plt.grid(True)
plt.show()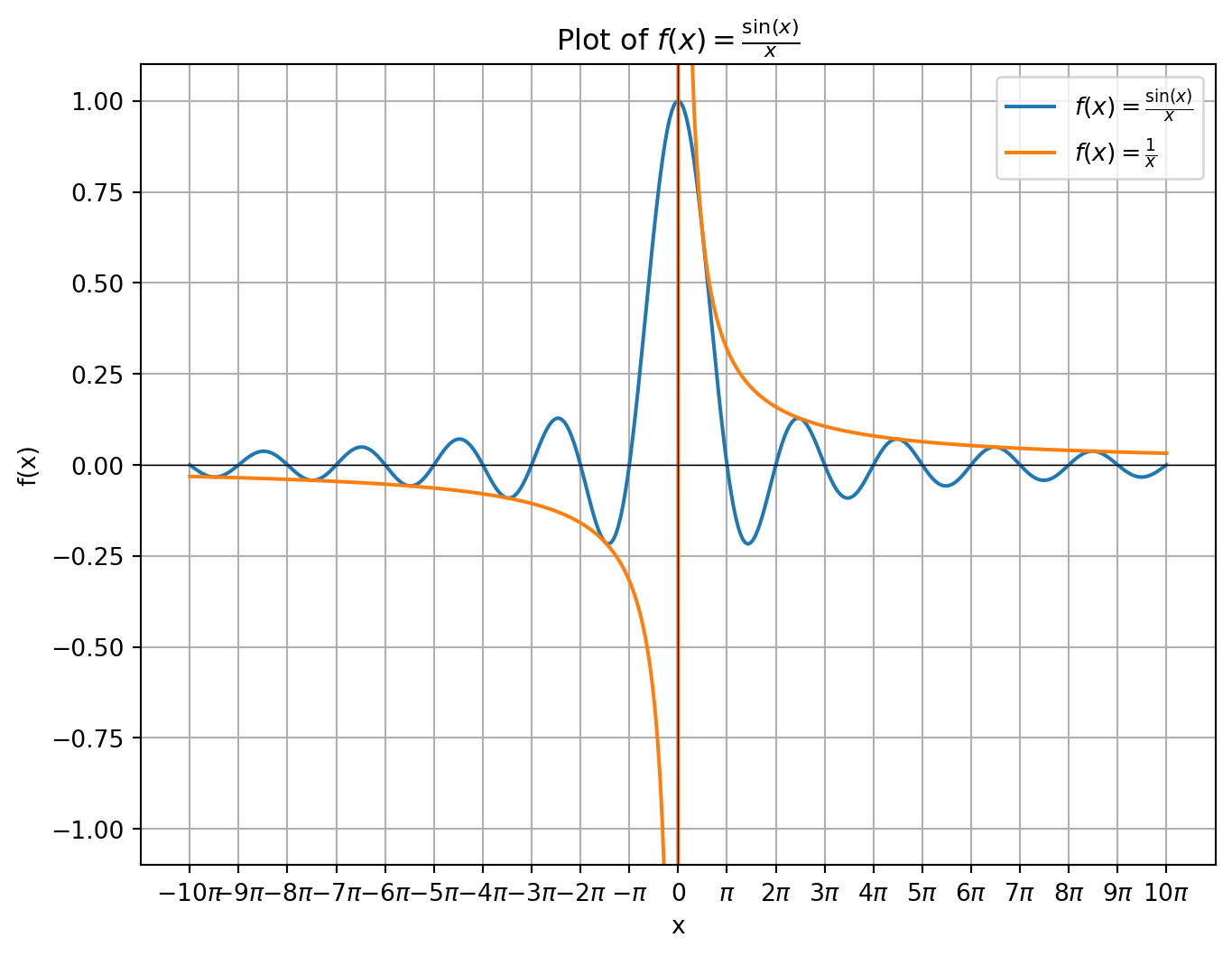

Figure 3

▶  \(x = 0\)における連続性の証明

Proof

偶関数の性質

\[ \frac{\sin x}{x} = \frac{\sin -x}{-x} \]

より \(0 < x \to +0\) の場合を考えます．xy座標上に \(O = (0, 0)，A = (1, 0)，B = (\cos x, \sin x)，C = (1, \tan x)\) という点をとったとき，

\[ \text{三角形}OAB \subset \text{扇形}OAB \subset \text{三角形}OAC \]

つまり

\[ \text{三角形}OAB\text{の面積} \leq \text{扇形}OAB\text{の面積} \leq \text{三角形}OAC \]

従って，

\[ \begin{align} \frac{\sin x}{2} \leq \frac{x}{2} < \frac{\tan x}{2} \end{align} \]

両辺 を \(\sin ⁡x\) で割って逆数をとると

\[ \begin{align} \cos x \leq \frac{x\sin x}{x} < 1 \end{align} \]

ここで，\(x\to +0\) とすると，\(\cos x \to 1\) となり，はさみうちの原理より

\[ \lim_{x\to+0}\frac{\sin x}{x} = 1 \]

▶  \(x = 0\)における微分可能性の証明

Proof

\[ \begin{align} \cos x \leq \frac{x\sin x}{x} < 1 \end{align} \]

が \(-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}\) で成り立つので

\[ 0=\lim_{x\to0}\frac{\cos(x)-1}{x}\le\lim_{x\to0}\frac{\frac{\sin(x)}x-1}{x-0}\le0 \]

\[ \begin{align} \lim_{x\to0}\frac{1-\cos(x)}x &=\lim_{x\to0}\frac1x\frac{\sin^2(x)}{1+\cos(x)}\\ &=\lim_{x\to0}\frac{\sin(x)}x\lim_{x\to0}\frac{\sin(x)}{1+\cos(x)}\\[6pt] &=1\cdot0 = 0 \end{align} \]

従って，はさみうちの原理より \(f^\prime(0) = 0\)