Exercise 1
\(\tan {75}^\circ\) を求めよ
\[ \begin{align} \tan {45}^\circ &= 1\\ \tan {30}^\circ &= \frac{\sqrt{3}}{3} \end{align} \]
より,加法定理を用いて
\[ \begin{align} \tan {75}^\circ &= \frac{\tan{30}^\circ + \tan{45}^\circ}{1 - \tan{30}^\circ\tan{45}^\circ}\\ &= \frac{1 + \frac{\sqrt{3}}{3}}{1 - \frac{\sqrt{3}}{3}}\\ &= 2 + \sqrt{3} \end{align} \]
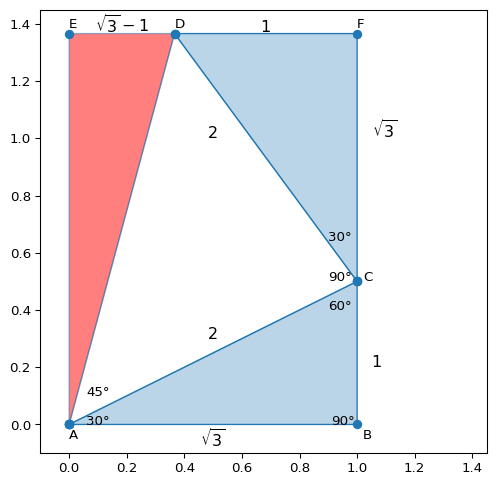
\(\angle A = {30}^\circ, \angle B = {90}^\circ, \angle C = {60}^\circ\) の \(\triangle ABC\) を考えたとき,\(\angle A\) の斜辺 \(AC\) を用いて 直角二等辺三角形 \(\triangle ACD\) をまず作成します.
この点 \(D\) を通るように \(AB\) と平行な線を引き,長方形 \(AEFB\) を以下のように作成します.
Code
import shapely.plotting
import matplotlib.pyplot as plt
from shapely.geometry import Polygon
import numpy as np
A = (0, 0)
B = (1, 0)
C = (1, np.sin(np.radians(30)))
D = (np.sqrt(2) * np.cos(np.radians(75)), np.sqrt(2) * np.sin(np.radians(75)))
E = (0, np.sqrt(2) * np.sin(np.radians(75)))
F = (1, np.sqrt(2) * np.sin(np.radians(75)))
polygon1 = Polygon([A, B, C])
polygon2 = Polygon([A, C, D])
polygon3 = Polygon([A, E, D])
polygon4 = Polygon([C, D, F])
fig, ax = plt.subplots(figsize=(6, 6))
shapely.plotting.plot_polygon(polygon1, ax=ax)
shapely.plotting.plot_polygon(polygon2, alpha=0.5, facecolor='none', ax=ax)
shapely.plotting.plot_polygon(polygon3, alpha=0.5, facecolor='red', ax=ax)
shapely.plotting.plot_polygon(polygon4, ax=ax)
# 軸の範囲を設定
plt.xlim(-0.1, 1.45)
plt.ylim(-0.1, 1.45)
# add label
plt.text(A[0], A[1] - 0.05, 'A')
plt.text(B[0]+0.02, B[1] - 0.05, 'B')
plt.text(C[0]+0.02, C[1], 'C')
plt.text(D[0], D[1] + 0.02, 'D')
plt.text(E[0], E[1] + 0.02, 'E')
plt.text(F[0], F[1] + 0.02, 'F')
# Add Angles
ax.text(A[0] + 0.06, A[1], f"{30}°", fontsize=10)
ax.text(A[0] + 0.06, A[1] + 0.1, f"{45}°", fontsize=10)
ax.text(B[0] - 0.09, B[1], f"{90}°", fontsize=10)
ax.text(C[0] - 0.1, C[1], f"{90}°", fontsize=10)
ax.text(C[0] - 0.1, C[1] + 0.14, f"{30}°", fontsize=10)
ax.text(C[0] - 0.1, C[1] - 0.1, f"{60}°", fontsize=10)
# Add length
ax.text(0.5, -0.08, "$\sqrt{3}$", fontsize=12, color="black", horizontalalignment="center")
ax.text(0.5, 0.3, "2", fontsize=12, color="black", horizontalalignment="center")
ax.text(0.5, 1.0, "2", fontsize=12, color="black", horizontalalignment="center")
ax.text(1.05, 0.2, "1", fontsize=12, color="black", horizontalalignment="left")
ax.text(1.05, 1.0, "$\sqrt{3}$", fontsize=12, color="black", horizontalalignment="left")
ax.text((D[0] + F[0])/2, 1.37, "1", fontsize=12, color="black", horizontalalignment="center")
ax.text((D[0] + E[0])/2, 1.37, "$\sqrt{3} - 1$", fontsize=12, color="black", horizontalalignment="center")
plt.show()このとき, \(\triangle CFD \equiv \triangle ABC\) なので
- \(AE = 1 + \sqrt{3}\)
- \(DE = \sqrt{3} - 1\)
であることがわかります.\(\triangle ACD\) は直角二等辺三角形なので \(\angle ADC = {45}^\circ\).従って,
\[ \angle ADE = {75}^\circ \]
よって,
\[ \begin{align} \tan{75}^\circ &= \frac{1 + \sqrt{3}}{\sqrt{3} - 1} \\ &= \frac{4 + 2\sqrt{3}}{2}\\ &= 2 + \sqrt{3} \end{align} \]