敵の砲台の座標を探せ 1/N

幾何
Author

Ryo Nakagami

Published

2025-03-02

円の式

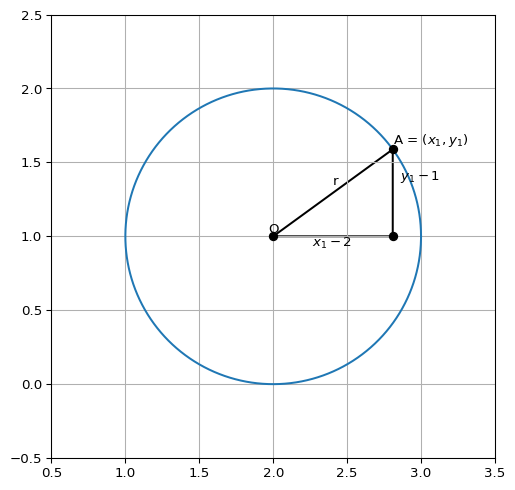
\((a, b)\) を中心点とする半径 \(r\) の円をplotすることを考えます．

半径 \(r\) の円の中心点の座標が原点 \((0, 0)\) にある場合，円周上の点 \(P = (x, y)\) は，\(P\) から \(x\) 軸に下ろした垂線と \(x\) 軸が交わる点を \(Q\) としたとき \(\triangle OPQ\) は斜辺 \(r\)，高さ \(y\), 底辺の長さ \(x\) となる直角三角形を構成するので，三平方の定理より

\[ r^2 = x^2 + y^2 \]

これが円上の座標が満たす方程式となります．原点を中心点とする場合を考えましたが，中心が \((a, b)\)，半径 \(r\) の円の式は同様の方法で

\[ r^2 = (x - a)^2 + (y - b)^2 \label{#eq-circle} \]

と表すことが出来ます．

Code 
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.tri as mtri

# set params
R = 1
O = (2, 1)

# variables
theta = np.linspace(0, 2 * np.pi, 1000)
x = np.cos(theta) * R + O[0]
y = np.sin(theta) * R + O[1]

A = (x[100], y[100])
triangles = [[0, 1, 2]]
x_trinagle = [O[0], A[0], A[0]]
y_trinagle = [O[1], O[1], A[1]]
triang = mtri.Triangulation(x_trinagle, y_trinagle, triangles)

# plot
fig, ax = plt.subplots(figsize=(8, 6))
ax.grid()
ax.set_aspect("equal")
ax.set_xlim(0.5, 3.5)
ax.set_ylim(-0.5, 2.5)


ax.plot(x, y)
ax.scatter(*O, s=8, color="k")
ax.scatter(*A, s=8, color="k")
ax.text(*O, s="O",  ha='center', va='bottom')
ax.text(*A, s="A = ($x_1, y_1$)", ha='left', va='bottom')
ax.text(2.4, 1.35, s="r")
ax.text(2.4, 0.9, s="$x_1 - 2$", ha='center', va='bottom')
ax.text(A[0]+0.05, 1.35, s="$y_1 - 1$", ha='left', va='bottom')

# add lines
ax.triplot(triang, 'ko-')


plt.show()

３点を通る円の方程式

Code 
# set params
R = 2.5
O = (3, 1/2)

# variables
theta = np.linspace(0, 2 * np.pi, 1000)
x = np.cos(theta) * R + O[0]
y = np.sin(theta) * R + O[1]

P = (1, -1)
Q = (3, 3)
R = (1, 2)

# plot
fig, ax = plt.subplots(figsize=(8, 6))
ax.grid()
ax.set_aspect("equal")

ax.plot(x, y)
ax.scatter(*O, s=8, color="k")
ax.scatter(*P, s=8, color="k")
ax.scatter(*Q, s=8, color="k")
ax.scatter(*R, s=8, color="k")
ax.text(*O, s="O",  ha='center', va='bottom')
ax.text(*P, s="P",  ha='center', va='bottom')
ax.text(*Q, s="Q", ha='left', va='bottom')
ax.text(*R, s="R", ha='left', va='bottom')


plt.show()

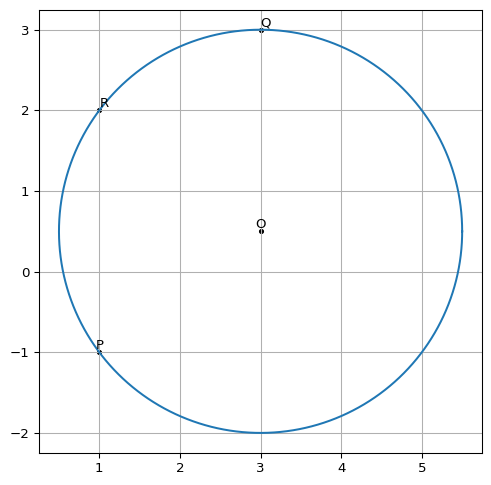
３点 \(P = (1, -1), Q = (3, 3), R = (1, 2)\) が与えられたとして，この３点を通る円を求める問題を考えます．

\(\eqref{#eq-circle}\) を展開すると

\[ x^2 + y^2 - 2ax - 2by + a^2 + b^2 = r^2 \]

これを整理して

\[ x^2 + y^2 + Ax + By + C = 0 \label{#eq-basemodel} \]

と変形します．ここで，\(P = (1, -1), Q = (3, 3), R = (1, 2)\) の情報を用いると

\[ \begin{gather} 2 + A - B + C = 0\\ 18 + 3A + 3B + C = 0\\ 5 + A +2B + C = 0 \end{gather} \]

という \(A,B,C\) についての連立方程式を得ることが出来ます．これを解くと

\[ A = -6, B = -1, C = 3 \]

従って，

\[ (x - 3)^2 + (y - 0.5)^2 = 2.5^2 \label{#eq-ans1} \]

外接円から求める

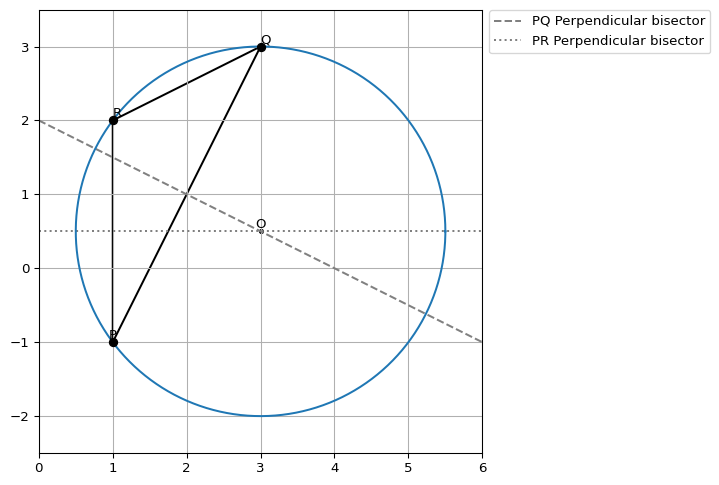
点 \(P, Q, R\) からなる三角形の外接円として求めたい円を捉えることも出来ます． 外接円の円心は三角形の各線分の垂直二等分線の交点として求めることが出来ます．

Code 
def func_pq(x):
    a = - (P[0] - Q[0]) / (P[1] - Q[1])
    b = - a * (P[0] + Q[0]) / 2 + (P[1] + Q[1]) / 2

    return a*x + b

def func_pr(x):
    a = - (P[0] - R[0]) / (P[1] - R[1])
    b = - a * (P[0] + R[0]) / 2 + (P[1] + R[1]) / 2

    return a*x + b

x_lin = np.array([0, 6])
triangles = [[0, 1, 2]]
x_trinagle = [P[0], Q[0], R[0]]
y_trinagle = [P[1], Q[1], R[1]]
triang = mtri.Triangulation(x_trinagle, y_trinagle, triangles)



# plot
fig, ax = plt.subplots(figsize=(8, 6))
ax.grid()
ax.set_aspect("equal")
ax.set_xlim(0, 6)
ax.set_ylim(-2.5, 3.5)
ax.plot(x_lin, func_pq(x_lin), label='PQ Perpendicular bisector', linestyle='--', color='gray')
ax.plot(x_lin, func_pr(x_lin), label='PR Perpendicular bisector', linestyle=':', color='gray')


ax.plot(x, y)
ax.scatter(*O, s=8, color="k")
ax.scatter(*P, s=8, color="k")
ax.scatter(*Q, s=8, color="k")
ax.scatter(*R, s=8, color="k")
ax.text(*O, s="O",  ha='center', va='bottom')
ax.text(*P, s="P",  ha='center', va='bottom')
ax.text(*Q, s="Q", ha='left', va='bottom')
ax.text(*R, s="R", ha='left', va='bottom')

# add lines
ax.triplot(triang, 'ko-')

plt.legend(loc='center left', bbox_to_anchor=(1, 0.95))
plt.show()

\(PQ\) の垂直二等分線 \(f(x)\) は

\[ \begin{align} f(x) &= -\frac{P_x - Q_x}{P_y - Q_y}x + \frac{P_y + Q_y}{2} + \frac{P_x - Q_x}{P_y - Q_y} \frac{P_x + Q_y}{2}\\ &= -\frac{P_x - Q_x}{P_y - Q_y}x + \frac{P_x^2 - Q_x^2 + P_y^2 - Q_y^2}{2(P_y - Q_y)} \end{align} \]

同様に \(PR\) の垂直二等分線 \(g(x)\) は

\[ \begin{align} g(x) &= -\frac{P_x - R_x}{P_y - R_y}x + \frac{P_y + R_y}{2} + \frac{P_x - R_x}{P_y - R_y} \frac{P_x + R_y}{2}\\ &= -\frac{P_x - R_x}{P_y - R_y}x + \frac{P_x^2 - R_x^2 + P_y^2 - R_y^2}{2(P_y - R_y)} \end{align} \]

ここから \(f(x), g(x)\) が交差する点を求めることで外接円の円心を求めることが出来ます．

少しめんどくさいので，数値計算で説いてみると

Code 
a = - (P[0] - Q[0]) / (P[1] - Q[1])
b = - a * (P[0] + Q[0]) / 2 + (P[1] + Q[1]) / 2
c = - (P[0] - R[0]) / (P[1] - R[1])
d = - c * (P[0] + R[0]) / 2 + (P[1] + R[1]) / 2

print((d-b)/(a-c), a * (d-b)/(a-c) + b)
3.0 0.5

\(\eqref{#eq-ans1}\) と一致する計算結果となることが確かめられました．

📘 REMARKS

上記の垂直二等分線の交点を \((x_0, y_0)\) としたとき，整理すると以下のようになります．

\[ A = \left(\begin{array}{cc} R_y - Q_y & -(P_y - Q_y)\\ -(R_x - Q_x) & P_x - Q_x\\ \end{array}\right) \]

としたとき，

\[ \left(\begin{array}{c} x_0\\ y_0 \end{array}\right) = \frac{1}{\operatorname{det}A} A\left(\begin{array}{c} (P_x^2 - Q_x^2 + P_y^2 - Q_y^2)/2\\ (R_x^2 - Q_x^2 + R_y^2 - Q_y^2)/2 \end{array}\right) \]

実際に計算してみると

Code 
A_array = np.array([[R[1] - Q[1], -(P[1] - Q[1])], [-(R[0] - Q[0]), P[0] - Q[0]]])
B_array = np.array(
    [
        [(P[0]**2 - Q[0]**2 + P[1]**2 - Q[1]**2) / 2],
        [(R[0]**2 - Q[0]**2 + R[1]**2 - Q[1]**2) / 2],
    ]
)

result = np.ravel((A_array @ B_array) / np.linalg.det(A_array))
radius = np.sqrt(np.sum((np.array(P) - result) **2))
print(f"中心点 = ({result}), 半径 = {radius}")
中心点 = ([3.  0.5]), 半径 = 2.5

敵の砲台の座標を探せ

Exercise 1

とある固定の１地点から自軍領地に対して敵が砲撃をかけてきているとします. 敵の砲台は角度のみを調整できるだけで，砲撃予定距離 \(r\) は一定とします．ただし，実際の砲撃距離は風向などの外乱要因によってノイズが混じっているとします．

とある日に敵から50回の攻撃を受けたとき，その砲台座標を推定してください．砲撃のノイズは\(\operatorname{i.i.d}\)とする．

\(\eqref{#eq-basemodel}\) より

\[ \begin{align} z_i = - x_i^2 - y_i^2 \end{align} \]

と定義すると，\(e_i\) をresidualとして

\[ z_i = \beta_0 + \beta_1 x_i + \beta_2 y_i + e_i \]

について \((\beta_0, \beta_1, \beta_2)\) をLinear modelで推定し，その推定値を \((\hat\beta_0, \hat\beta_1, \hat\beta_2)\) と表せば 敵の砲台の推定座標 \((\hat x, \hat y)\) 及び推定距離 \(\hat r\) は

\[ \begin{align} \hat x &= -\hat\beta_1/2\\ \hat y &= -\hat\beta_2/2\\ \hat r &= \sqrt{\hat x^2 + \hat y^2 - \hat\beta_0} \end{align} \]

と計算できそうに思えます．

▶  Data Generating Process

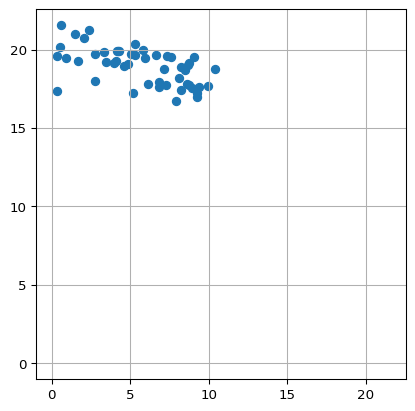
  • 敵の砲台の座標は \((0, 0)\)
  • 敵は \((0, 0)\) の地点から砲撃距離 \(20\) で攻撃してくる
  • 実際の砲撃距離 \(r \sim N(20, 1)\)
  • 砲撃角度は \(\left[\displaystyle{\frac{\pi}{3}, \frac{\pi}{2}}\right]\) の範囲で一様分布で定まる

というData Generating Processとします．

Code 
def gdp(x_0: float, y_0: float, noise: float = 1.0, radius: float = 20,  attack_num: int = 50):
    # params
    theta = np.random.uniform(np.pi/3 , np.pi/2 , attack_num)
    r = radius + np.random.normal(0, noise, attack_num)

    x = np.cos(theta) * r + x_0
    y = np.sin(theta) * r + y_0

    return x, y

このGDPに従う形で攻撃されたとするとき，その散布図は以下のようになります．

Code 
np.random.seed(42)

x_attack, y_attack = gdp(0, 0)

fig, ax = plt.subplots()
ax.scatter(x_attack, y_attack)
ax.set_xlim(-1, np.max([np.max(x_attack), np.max(y_attack)]) + 1)
ax.set_ylim(-1, np.max([np.max(x_attack), np.max(y_attack)]) + 1)
ax.grid()
ax.set_aspect('equal')
plt.show()

▶  OLS Monte Carlo Simulation

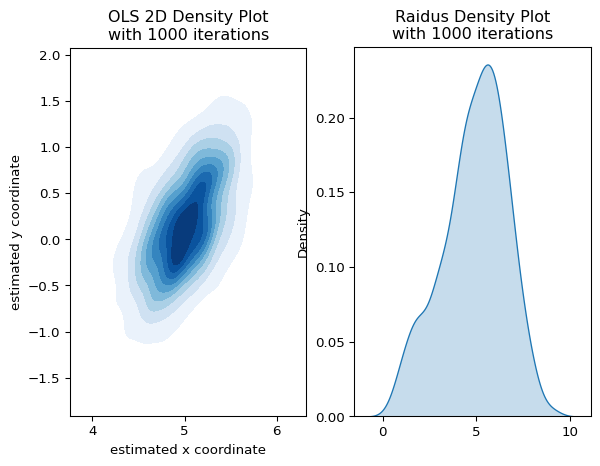
OLSによるパラメータ推定値を \(1,000\) 回simulationし，その組み合わせをkde plotしたものが以下となります．x座標についてバイアスがあることがわかります． 砲撃距離に関しても不自然な推定値となっています．

Code 
import pandas as pd
import statsmodels.api as sm
import seaborn as sns

def gpd_dataframe(x: float = 0, y: float = 0, noise: float = 1.0):
    x_attack, y_attack = gdp(x, y, noise)
    df = pd.DataFrame(
        {
            "x_coordinate": x_attack,
            "y_coordinate": y_attack,
        }
    )

    return df


def ols_solver(
    df: pd.DataFrame, xy_columns: tuple[str] = ("x_coordinate", "y_coordinate")
):
    Y = -(df[xy_columns[0]] ** 2) - df[xy_columns[1]]
    X = sm.add_constant(df.loc[:, xy_columns])

    # regression
    model = sm.OLS(Y, X)
    results = model.fit()

    # convert estimates to target params
    x_hat = -results.params[xy_columns[0]] / 2
    y_hat = -results.params[xy_columns[1]] / 2
    r_hat_sqr = (x_hat**2 + y_hat**2 - results.params['const'])
    r_hat = np.sqrt(r_hat_sqr) if r_hat_sqr > 0 else np.nan

    return [x_hat, y_hat, r_hat]


def estimator_simulator(func, noise: float = 1.0, iter: int = 1000):
    res = list(map(lambda x: func(gpd_dataframe(0, 0, noise)), range(iter)))
    return np.array(res)

fig, ax = plt.subplots(1, 2)

ols_res = estimator_simulator(ols_solver)
sns.kdeplot(x=ols_res[:, 0], y=ols_res[:, 1], cmap="Blues", fill=True, ax=ax[0])
sns.kdeplot(x=ols_res[:, 2], cmap="Blues", fill=True, ax=ax[1])

# Show the plot
ax[0].set_xlabel("estimated x coordinate")
ax[0].set_ylabel("estimated y coordinate")
ax[0].set_aspect('equal')
ax[0].set_title("OLS 2D Density Plot\nwith 1000 iterations")
ax[1].set_title("Raidus Density Plot\nwith 1000 iterations")
plt.show()

そもそも \(r_i = 20 + \epsilon_i\) と決定されていますが

\[ \beta_0 = a^2 + b^2 - (r + \epsilon_i)^2 \]

で決定されており，これを踏まえて OLSのモデルを見てみると

\[ z_i = \left(a^2 + b^2 - r^2 - \epsilon_i^2 - 2r\epsilon \right) - 2ax_i - 2by_i \]

となるので，そもそもunbiasedな推定量になっていないと判断できます

▶  Regression with MLE

\(\eqref{#eq-circle}\) に則り，もっと直接的に

\[ L(\beta) = (\sqrt{(x_i - \beta_1)^2 + (y_i - \beta_2)^2} - \beta_0)^2 \]

を最小する形でパラメーターを推定してみます．このとき．residualが\(N(0, \sigma)\) に従うならばLikelihoodは

\[ f(X_i\vert \beta, \sigma) = \frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{L(\beta)}{2\sigma^2}\right) \]

と表せるので，これを用いて解いてみます．

Code 
import numpy as np
from scipy.optimize import minimize


def lik(parameters, x, y):
    x_0 = parameters[0]
    y_0 = parameters[1]
    r_0 = parameters[2]
    sigma = parameters[3]
    g_x = (np.sqrt((np.sqrt((x - x_0) ** 2 + (y - y_0) ** 2) - r_0)**2)) ** 2

    L = len(x) / 2 * np.log(sigma**2) +  1 / (2 * sigma**2) * np.sum(g_x)
    return L


def mle_solver(
    df: pd.DataFrame, xy_columns: tuple[str] = ("x_coordinate", "y_coordinate")
):

    x_attack = df[xy_columns[0]].values
    y_attack = df[xy_columns[1]].values
    lik_model = minimize(
        lambda params: lik(params, x_attack, y_attack),
        np.array([1, 1, 20, 1]),
        method="L-BFGS-B",
    )
    return lik_model["x"]


mle_res = estimator_simulator(mle_solver)

# plot
fig, axes= plt.subplots(1, 2)

sns.kdeplot(x=mle_res[:, 0], y=mle_res[:, 1], cmap="Blues", fill=True, ax=axes[0])
sns.kdeplot(x=mle_res[:, 2], cmap="Blues", fill=True, ax=axes[1])

# Show the plot
axes[0].set_xlabel("estimated x coordinate")
axes[0].set_ylabel("estimated y coordinate")
axes[0].set_title("MLE 2D Density Plot\nwith 1000 iterations")
axes[0].set_aspect("equal")
axes[1].set_title("Raidus Density Plot\nwith 1000 iterations")

plt.show()

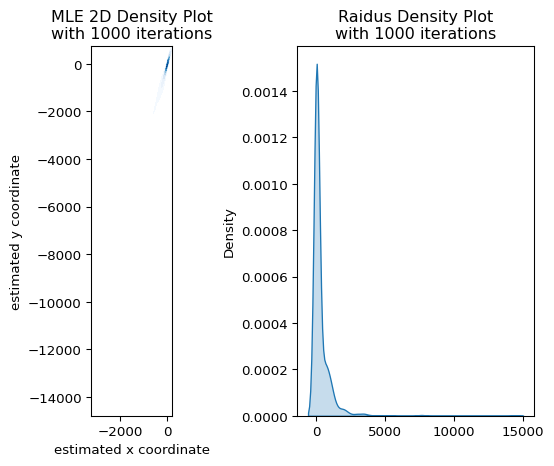
定式化は正しいはずですが，\((x_0, y_0, r_0)\) は効率的な推定量となっていない疑いがあることが読み取れます．

次に，

\[ L(\beta) = \sqrt{(x_i - \beta_1)^2 + (y_i - \beta_2)^2 - \beta_0^2} \label{#eq-mle} \]

をLoss functionとして推定してみます．

Code 
import numpy as np
from scipy.optimize import minimize


def lik(parameters, x, y):
    x_0 = parameters[0]
    y_0 = parameters[1]
    r_0 = parameters[2]
    sigma = parameters[3]
    g_x = (x - x_0) ** 2 + (y - y_0) ** 2 - r_0**2

    L = len(x) / 2 * np.log(sigma**2) +  1 / (2 * sigma**2) * np.sum(g_x)
    return L


def mle_solver(
    df: pd.DataFrame, xy_columns: tuple[str] = ("x_coordinate", "y_coordinate")
):

    x_attack = df[xy_columns[0]].values
    y_attack = df[xy_columns[1]].values
    lik_model = minimize(
        lambda params: lik(params, x_attack, y_attack),
        np.array([1, 1, 20, 1]),
        method="L-BFGS-B",
    )
    return lik_model["x"]


mle_res = estimator_simulator(mle_solver)

# plot
fig, axes= plt.subplots(1, 2)

sns.kdeplot(x=mle_res[:, 0], y=mle_res[:, 1], cmap="Blues", fill=True, ax=axes[0])
sns.kdeplot(x=mle_res[:, 2], cmap="Blues", fill=True, ax=axes[1])

# Show the plot
axes[0].set_xlabel("estimated x coordinate")
axes[0].set_ylabel("estimated y coordinate")
axes[0].set_title("MLE 2D Density Plot\nwith 1000 iterations")
axes[0].set_aspect("equal")
axes[1].set_title("Raidus Density Plot\nwith 1000 iterations")

plt.show()

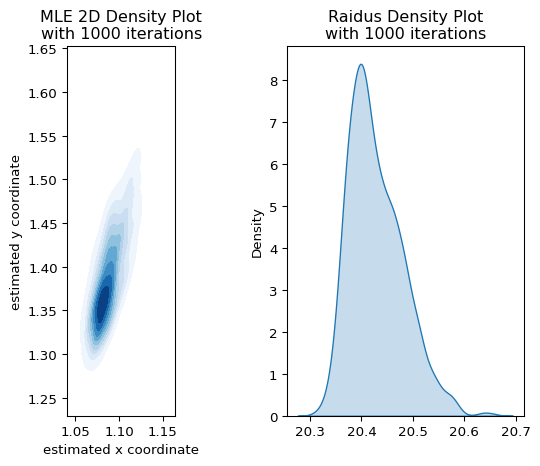
先程よりは精度良く推定できているように見えますが，\(\eqref{#eq-mle}\) は

\[ L(\beta) = \sqrt{\epsilon_i^2 + 2\beta_0 \epsilon_i} \]

となるので，そもそもMLEの定式化が間違っていることがわかります．また，\(\beta_0\) が大きいほどresidualが大きくなる傾向があることから，unbiasedな推定量は得られていないことがわかります．

▶  Regression with stan

cmdstanを用いて砲台座標を推定する例を紹介します．まずstan modelを以下のように設定します．

  • 砲撃距離のノイズについて \(N(0, 1)\) であることが既にわかっている状況を想定
  • 予定砲撃距離 \(r_0\) は \(\operatorname{Uniform}(2, 30)\) の事前分布がある
data {
    int<lower=1> N;  // Number of data points
    array[N] real y; // outcomes
    array[N] real x; // outcomes
}

parameters {
    real<lower=0> r_0; // probability of success
    real x_0;             // Center x-coordinate
    real y_0;             // Center y-coordinate
}

model {
    // priors
    r_0 ~ uniform(2, 30);
    real sigma = 1;

    // objective loss
    array[N] real circle_equation;
    for (i in 1:N) {
        circle_equation[i] = sqrt((x[i] - x_0)^2 + (y[i] - y_0)^2) - r_0;
    }

    circle_equation ~ normal(0, sigma);
}

その後，このモデルを用いて推定したものが以下となります．

from cmdstanpy import CmdStanModel

df_stan = gpd_dataframe(0, 0, 1)
data = {
    "N": df_stan.shape[0],
    "y": df_stan.y_coordinate.values,
    "x": df_stan.x_coordinate.values,
    "sigma": 1,
}

model = CmdStanModel(stan_file="./stanmodel.stan")
fit = model.sample(data=data, seed=42)
fit.summary()
09:43:42 - cmdstanpy - INFO - compiling stan file /home/runner/work/regmonkey-datascience-blog/regmonkey-datascience-blog/posts/2025-03-02-find-coordinates/stanmodel.stan to exe file /home/runner/work/regmonkey-datascience-blog/regmonkey-datascience-blog/posts/2025-03-02-find-coordinates/stanmodel
09:43:50 - cmdstanpy - INFO - compiled model executable: /home/runner/work/regmonkey-datascience-blog/regmonkey-datascience-blog/posts/2025-03-02-find-coordinates/stanmodel
09:43:50 - cmdstanpy - INFO - CmdStan start processing
                                                                                                                                                                                                                                                                                                                                
09:43:51 - cmdstanpy - INFO - CmdStan done processing.
09:43:51 - cmdstanpy - WARNING - Some chains may have failed to converge.
    Chain 1 had 310 divergent transitions (31.0%)
    Chain 2 had 341 divergent transitions (34.1%)
    Chain 3 had 293 divergent transitions (29.3%)
    Chain 4 had 321 divergent transitions (32.1%)
    Use the "diagnose()" method on the CmdStanMCMC object to see further information.
Mean MCSE StdDev MAD 5% 50% 95% ESS_bulk ESS_tail R_hat
lp__ -22.627700 0.044143 1.21901 0.873029 -25.04740 -22.267300 -21.44630 886.927 1292.320 1.00150
r_0 20.167700 0.429917 6.21166 7.274600 9.15979 20.889900 29.01690 208.132 258.641 1.01910
x_0 0.151580 0.131551 1.88887 1.973310 -3.05708 0.195963 3.10467 199.726 234.533 1.02554
y_0 -0.299075 0.419656 6.11452 7.154340 -8.93022 -1.015920 10.49850 220.609 278.533 1.01959

Credible intervalを見ると \((0, 0)\) は推定区間に含まれている一方，Mean, Medianともに \(y_0\) の方は乖離した値が推定されてしまっています．