Key Takeaways
- 冷凍装置は,蒸発器で周囲から熱を取り入れ,圧縮機で動力を加えて凝縮器で熱を周囲へ排出する装置のこと
- 冷媒とは,冷凍サイクルの中で熱の輸送に使われる媒体のこと
ものを冷やす仕組み
熱は常に「高温から低温へ移動(=熱力学第二法則)」します.この性質を利用して,冷却は次のように行われます:
- 対象物よりも温度の低いものを接触させて熱を移動させる = 熱伝導ベース
- 蒸発や断熱膨張などの物理現象を利用して,周囲から熱を奪う = 相変化ベース
ものを冷やすのは熱伝導ベースと相変化ベースの2つがありますが,冷却効率は大きく異なります.
| 熱の種類 |
顕熱(温度変化) |
潜熱(状態変化) |
| 冷却効率(J/g) |
例:1gの水を用いて10℃分熱を吸収する → 約42 J/g吸収 |
水1gの蒸発 → 約2260 J/g吸収 |
| エネルギー吸収 |
小さい(比熱×温度差に依存) |
大きい(潜熱は比熱の数十倍) |
| 使用例 |
冷水で冷やす,金属板で放熱など |
汗の蒸発,気化式冷却,打ち水 |
同じ質量の水を使っても,蒸発させた方がはるかに多くの熱エネルギーを奪えるため,冷却効率が高いという特徴が有ります.
- 1kgの冷水が \(4.1916\) kJ の熱を取り入れると,1Kだけ温度が上昇する.
- 水を20℃→30℃に温めるときに使う熱は「顕熱」
- 物質1kgの温度を1K上げるのに必要な熱量は「比熱」
- 物質が状態変化(固体⇄液体⇄気体)するときに温度を変えずに出入りする熱は「潜熱」
- 熱運動の激しさを変化させるのではなく,分子間の結合をほどくために使われる熱
- 融解熱や蒸発熱
Example 1 顕熱
比熱 \(c\) [kJ/kg・K], 質量 m[kg],温度 \(t_1\) [K] の物質が熱を吸収して \(t_2\) になったとき,吸収した熱量 \(Q\) [kJ] は
\[
Q = m\cdot c(t_2 - t_1)
\]
と計算できます.
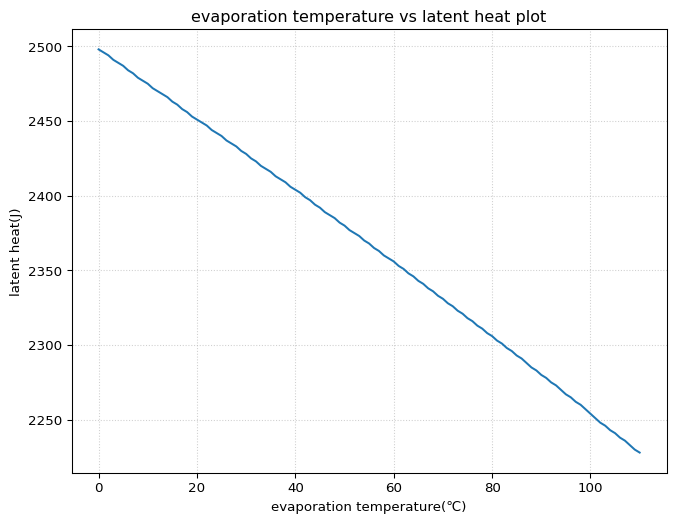
Example 2 水1gの潜熱
水は極性分子で,水素結合が強いため,蒸発に多くのエネルギーが必要という特徴が有ります.
Code
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('./input.csv')
temp = df['temp']
enthalpy = df['enthalpy'] * 1000
# pa = df['Pa']
plt.figure(figsize=(8, 6))
plt.plot(temp, enthalpy)
# 軸ラベルとタイトル
plt.xlabel('evaporation temperature(℃)')
plt.ylabel('latent heat(J)')
plt.title('evaporation temperature vs latent heat plot')
plt.grid(True, linestyle=':', alpha=0.6)
plt.show()
マクロの状態変数
- 熱力学とは,「非道にたくさんの分子からなる集団を1つの系と見て,これをマクロ的または統計的に調べる学問」
- 空気などの気体を体積 \(V\) のある容器に入れたとき,夥しい気体分子が容器の中でそれぞれ動いている(ミクロ的視点)
- この気体のマクロ的状態を表す量として圧力 \(p\) と絶対温度 \(T\) がある
ミクロとマクロの関係
- 圧力 \(p\): ものすごい数の気体分子が単位時間・単位面積当たり,容器の壁面に衝突して与えられる力積(\(\text{力} \times \text{時間}\))の平均的な送料
- 温度 \(T\): 気体分子の不規則な運動の平均的な激しさの度合い
絶対零度
- すべての分子が不規則な運動をやめて静止している状態
0℃以下の低温までものを冷やしたいとき → 冷媒の登場
熱を取り除きたいときは,蒸発潜熱を利用した冷却が効率が良いとわかりましたが,常圧のもとでは水は 100℃で沸騰,蒸発となります(標準沸点が100℃).一方,絶対圧 0.6108 kPa のような低圧にすれば 0℃で水は沸騰→蒸発しますが,
- ものを0℃まで冷やしたい場合は,この圧力を保つことが必要 → 高性能な真空ポンプが必要
- 0℃以下まで冷やしたいとしても,0℃で水は凍ってしまうので,0℃以下の低温を得ることはできない(熱力学第二法則)
0℃以下の低温を得るには,あまり高真空にすることなく,低い温度で沸騰・蒸発し,しかも蒸発潜熱の大きい物質を媒体として選ば良いとなります. このような熱を取り去る媒体を冷媒といいます.
Definition 1 (冷媒)
冷媒(refrigerant)とは,蒸発・凝縮などの相変化を通じて熱を運ぶ物質であり,主に冷凍機やエアコン,ヒートポンプで使われます. 蒸気圧圧縮冷凍装置で用いられる冷媒として,アンモニアやフルオロカーボン(R 134 a, R410 aなど)がある.
冷媒に求められる性質
- 毒性及び燃焼性が低く,安全性に優れること
- 地球環境や周囲環境を破壊しないこと
- 化学的に安定であること
- 適切な沸点を持つこと
- 経済性および入手性に優れること
- 単位面積あたりの冷凍能力が大きいこと(蒸発潜熱が大きい冷媒を使っていても,熱伝導率が悪かったり,流速が遅いと単位面積あたりの冷凍能力は小さい可能性がある)
- 理論成績係数が高いこと
- 圧縮機吐出しガス温度が冷凍機油の使用温度範囲内であること
- 伝熱特性に優れること
冷媒の種類
蒸気圧縮冷凍装置が出現した初期は,メチルエーテル,エチルエーテル,アンモニア,二酸化硫黄,メチルクロライドなどが冷媒として使用されていましたが,燃焼性や毒性という問題が有りました.
1928年にアメリカで無毒の不燃性のフルオロカーボン冷媒(R12)が発明され,産業用/家庭用の冷蔵庫や冷凍空調装置が普及するようになりました.冷媒は基本的にはフルオロカーボンとその他(自然冷媒)に分類されるほど普及しています.フルオロカーボンは,炭化水素の水素を一部フッ素に置き換えた化合物です.分子構造の特徴によりCFC,HCFC,HFC,HFO等のグループに分けられます.
フルオロカーボン冷媒の種類
| CFC冷媒 |
R11, R12 |
塩素を含むクロロフルオロカーボン冷媒.モントリオール議定書での規制対象.1995年末の段階で日本では全廃されている |
| HCFC冷媒 |
R22, R123 |
塩素を少量だけ含むハイドロクロロフルオロカーボン冷媒.2020年に日本では全廃 |
| HFC冷媒 |
R32, R125, R134a,R410A |
塩素を含まないハイドロフルオロカーボン冷媒.HFC冷媒は,HCFC冷媒と比べると誘電率が大きく,その電気絶縁性がやや劣る(圧縮機からの漏れ電流には注意を要する) |
フルオロカーボン冷媒とアンモニア冷媒の比較
- 冷凍効果という点ではアンモニアが圧倒的に優れる
- フルオロカーボン冷媒は冷凍効果は低めだが,安全性や取り扱いやすさから広く使われている
| 冷凍効果(潜熱) |
◎ 非常に高い |
△ 中程度 |
| 熱伝導率 |
◎ 高い |
△ 低い |
| 冷媒量 |
◎ 少量で済む |
△ 多く必要 |
| 圧力 |
○ 中〜高圧 |
○ 中圧(使いやすい) |
| 安全性 |
× 毒性・可燃性あり |
◎ 無毒・非可燃(だがGWP高) |
| 環境性 |
◎ ODP/GWP=0 |
△ GWP高いものが多い |
| 用途 |
産業用冷凍(冷凍倉庫など) |
家庭・車・業務用エアコンなど |
塩素を含むフルオロカーボン冷媒が大気中に放出されると,太陽からの強い紫外線によって分解され塩素 Cl を放出します. これがオゾン \(\text{O}_3\) と以下のような化学反応を行って,オゾンを分解・破壊してしまいます
\[
\begin{align}
\text{Cl} + \text{O}_3 &\to \text{CIO} + \text{O}_2\\
\text{ClO} + \text{O} &\to \text{CI} + \text{O}_2 \text{(再びオゾンを破壊してしまうClを生成)}
\end{align}
\]
- CIO: 一酸化塩素,常温常圧で気体であり,非常に不安定
冷媒の番号
冷媒番号はアシュレイ番号ともよばれ,冷媒の記号は先頭に「R」をつけて,2~4桁の数字を用いて表します.表記方法はASHRAE規格34及びISO817によって以下のように定められています
| R |
冷媒(Refrigerant)の頭文字 |
| 千の位 |
不飽和炭化水素に対する不飽和炭素結合の数(二重結合・三重結合など) |
| 百の位 |
炭素原子の数 − 1 |
| 十の位 |
水素原子の数 + 1 |
| 一の位 |
フッ素原子の数 |
| 添え字 |
構造異性体(同じ組成式だが結合の構造が異なる)または混合物の組成を区別するための記号 |
- プロパン冷媒(R290): \(\text{C}_3\text{H}_8\)
- R32: \(\text{C}\text{H}_2\text{F}_2\)
ただし,すべてがこのルールに則っているわけではなく,400番台は非共沸混合冷媒,500番台は共沸混合冷媒を示します.これらの場合,番号の下2桁はASHRAE規格で認定された冷媒番号の取得順となります.
600番台は有機化合物,700番台は無機化合物を示します.そのため,二酸化炭素やアンモニアなどの無機化合物には700番台が与えられます.例として,Nブタン冷媒R600,アンモニアR717,二酸化炭素R744です.
フルオロカーボン冷媒の「単一成分冷媒」をいくつか混ぜ合わせた「混合冷媒」があり,混合冷媒は「非共沸点混合冷媒」と「共沸混合冷媒」に分けられます.非共沸混合冷媒は沸点の異なる冷媒同士を混ぜ合わせた冷媒のことです.
- 相変化のとき温度勾配が生じる
- 露点(凝縮始め)と沸点(凝縮終わり)が一致しない
という特徴が有ります.一方,温度勾配を生じないのが「共沸混合冷媒」(R507A)です.温度勾配の小さい「非共沸混合冷媒」は「共沸混合冷媒」に近い凝縮蒸発特性があるので「疑似共沸混合冷媒」(R410A と R404A)とも呼ばれたりします.
フルオロカーボン冷媒の取り扱い
- フルオロカーボンは安定した冷媒で,毒性は低く,可燃性もないが酸欠の危険がある
- 大気中で空気より重く,濡れると床面付近に滞留しやすい
- 冷媒設備の全冷媒充填量(kg)を,冷媒を内蔵している機器を設置した最小室内陽席(m³)で除した値が,限界濃度以下であること
- 圧力容器や配管の修理の際に,内部に残留ガスがないことを確かめること
- 裸火や高温の物体に触れると,分解してフッ化水素やホスゲンなどの毒性の強いガスを生成する
- フルオロカーボン冷媒が濡れて滞留している室内に燃焼危惧があると不完全燃焼となり,一酸化炭素中毒のおそれがある
- 限界濃度とは,この濃度において湿疹や重大な障害を受けることなく,緊急の処置をとった上で,自らも避難できる程度の濃度
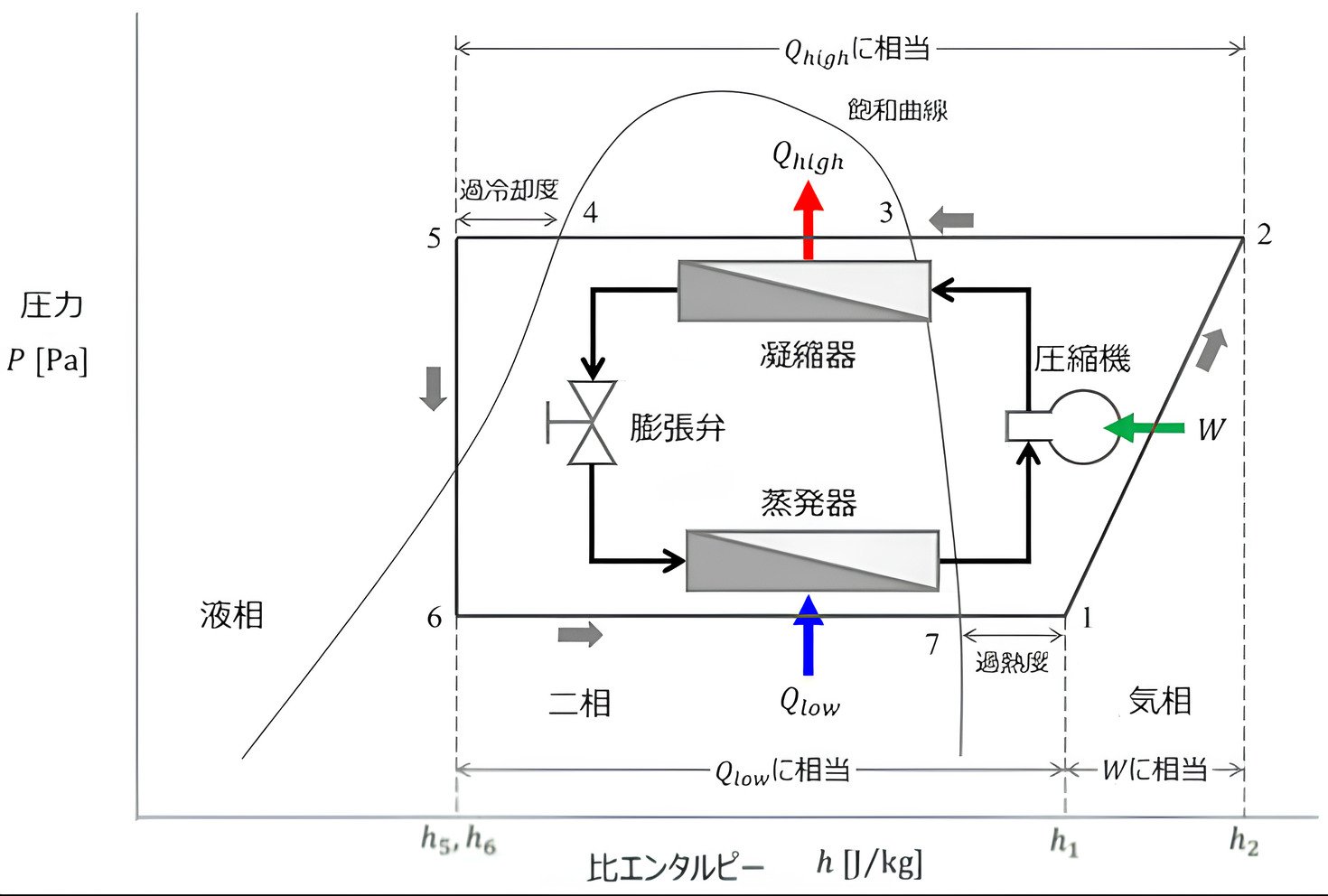
蒸発器・凝縮器・圧縮機・膨張弁
冷凍装置において,冷媒の蒸発潜熱を利用して物を冷却するには,冷媒と物とを直接接触させずに,冷却館内や容器内で冷媒を沸騰・蒸発させ.その壁(例: 配管壁)を介して冷却します.このような冷却管や容器で構成されたものを蒸発器といいます.
熱吸収した冷媒蒸気を蒸発器から取り除かなれば,一定の蒸発温度を維持することができなくなってしまいます.そのため発生した冷媒蒸気を蒸発器から常に取り除かなければなりません.熱吸収した冷媒蒸気を捨て去ってもいいですが,経済的ではないのでどうにか再利用する方法を模索する必要が有ります.
冷媒が沸騰・蒸発する温度(飽和温度)は圧力が下がるに伴って低下,逆に圧力上がると飽和温度も上昇します.この性質を活用し,蒸発器内で発生した蒸気に対して圧力を加える + 周囲(例: 外気温)から得られる外気や水で冷却(=潜熱を開放)して再び液化します.
このように冷媒は装置内を蒸発,圧力上昇,液化,膨張,再蒸発といった状態変化を繰り返しながら循環し,目的の冷凍作用を行います. この過程のことを冷凍サイクルと呼びます.
📘 REMARKS
| 蒸発器 |
低圧の液体冷媒が熱を吸収して蒸発し,周囲から熱を奪うことで冷却を行う熱器 |
| 圧縮機 |
蒸気が凝縮する圧力まで高めるために用いられる機器.空調機のの消費電力の約8割を占める |
| 凝縮器 |
高圧・高温の冷媒蒸気を冷却し,凝縮させる伝熱管や容器で構成された機器 |
| 膨張弁 |
圧力が高い凝縮器と圧力が低い蒸発器を結び通路の弁.凝縮した高圧の冷媒液を,低圧の蒸発器で蒸発した量だけ弁を調整して補給することで,蒸発器内を一定の低い圧力に保つ |
| 1 |
蒸発器をでて圧縮機に吸入される冷媒ガスは乾燥飽和蒸気より少し過熱された過熱蒸気(低圧) |
| 2 |
圧縮機から吐出され,凝縮器に入る冷媒蒸気はかなり温度の高い過熱蒸気(高圧) |
| 5 |
凝縮器で飽和液が少し過冷却され,膨張弁に入る過冷却液(高圧) |
| 6 |
膨張弁を通って減圧され,蒸発器に入る湿り蒸気(低圧) |
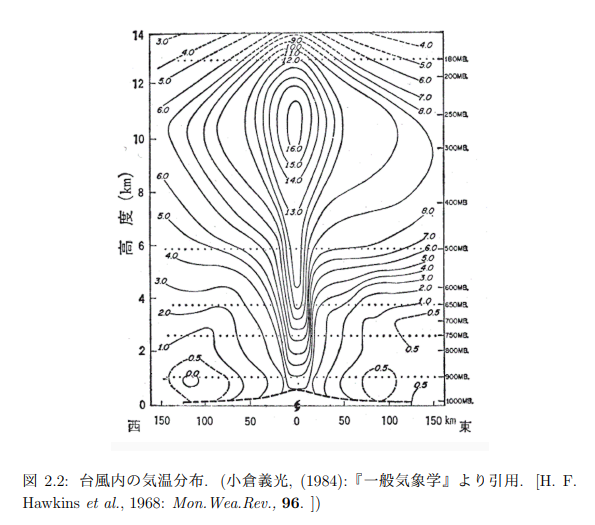
気体から液体に戻るとき,潜熱が開放されて周囲を温めます.身の回りの例として,台風の中心には強い上昇気流があり,それによって空気に含まれている水蒸気が上空に運ばれてと飽和し,そこで凝結(雲の状態へ)します.このとき潜熱を放出するので,台風中心の上空の空気は,その周りの平均気温よりも高くなっています.
上の図はx軸が台風の中心からの距離,y軸が高度及び気圧を指しています.等高線みたいな線は気候学的な高度別平均気温との差(温度偏差)をplotしています.
蒸発器と凝縮器におけるエンタルピー変化
理論冷凍サイクルにおいて,冷媒の蒸発及び凝縮は圧力一定のもとで行われます.比エンタルピー変化が
\[
dh = dq + vdp
\]
であるので,圧力一定であるので \(dp=0\) であることから
\[
dh = dq
\]
つまり,授受した熱量に相当する分だけ比エンタルピーが変化することがわかります.
冷凍装置の効率係数
圧縮機の仕事量
圧縮機に流出入する冷媒1kgが保有するエネルギーは,運動エネルギーや位置エネルギーが十分小さく無視できるとすると以下のように表せます
\[
\underbrace{h}_{\text{比エンタルピー}} = \underbrace{u}_{\text{内部エネルギー}} + \underbrace{p\nu}_{\text{冷媒流動の仕事}}
\]
- \(h\): 流動する冷媒の保有エネルギー [kJ/kg]
- \(u\): 物体を構成している膨大な数の分子・原子のもつエネルギーの総和として,物体内に蓄えられているエネルギー
- 熱エネルギーと分子・原子などの平均配置を決める相互作用エネルギー
- \(p\): 圧力
- \(\nu\): 比体積(冷媒蒸気1kgの体積) [\(m^3\)/kg]
したがって,以下のように変数を整理すると
- \(q_m\) [kg/s] : 圧縮機に単位時間に流出入する冷媒流量
- \(h_1\): 圧縮機入口の冷媒の比エンタルピー
- \(h_2\): 圧縮機出口の冷媒の比エンタルピー
圧縮機によって冷媒に加えられる単位時間あたりの圧縮仕事 \(P\) [kW] は以下のように表すことができます
\[
P = q_m(h_2 - h_1)
\]
蒸発器の熱交換量
蒸発器においては,冷媒は熱を組み上げ,その量だけ保有エネルギーが増大します.冷媒 1kg あたりが組み上げる熱量(冷凍効果)[kJ/kg]を \(r\) とすると
- \(h_1\): 蒸発器出口の冷媒の比エンタルピー
- \(h_6\): 入口の比エンタルピー
を用いて,
\[
r = h_1 - h_6
\]
また,単位時間あたりの交換熱量 \(\Phi_o\) は
\[
\Phi_o = q_m(h_6 - h_1)
\]
つまり,冷凍装置の冷凍能力は,蒸発器出入り口における冷媒の比エンタルピー差に冷媒循環量を乗じて求められることになります.
凝縮器の熱交換量
凝縮器では冷媒は熱放出し,その単位時間あたりの放出熱量 \(\Phi_k\) [kW] を凝縮負荷と呼びます.
- \(h_2\): 凝縮器入口の冷媒比エンタルピー
- \(h_5\): 凝縮器出口の冷媒比エンタルピー
より
\[
\Phi_k = q_m(h_2 - h_5)
\]
膨張弁では基本的に外部と熱交換を行いません.高圧・高温の液冷媒を断熱膨張を通して低圧・低温の液冷媒に変えるのが主な機能です. 冷媒液が圧力降下するときに,液の一部が自己蒸発する際の潜熱によって,冷媒自身の温度が下がります.
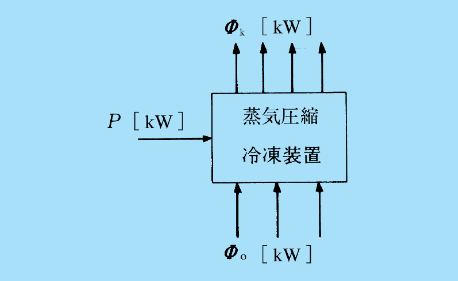
熱力学第一法則(エネルギー保存則)
単位時間あたりに冷凍装置に入るすべてのエネルギーは,単位時間あたりに装置から出るすべてのエネルギーと等しくなければなりません.ここから次の式が成立します:
\[
\Phi_k = \Phi_o + P
\]
Definition 2 (冷凍サイクルの成績係数)
冷凍作用を行うのに必要なエネルギー \(P\) と冷凍能力 \(\Phi_o\) の比を冷凍サイクルの成績係数(\(COP_c\))といい
\[
COP_c = \frac{\Phi_o}{P}
\]
この値は同じ冷凍装置であっても,運転条件によって変わります.
冷凍サイクルの成績係数が大きいほど小さい動力で大きな冷凍能力が得られると解釈できます.
実際の圧縮機では,
- 吸い込み弁と吐出し便の流れの抵抗
- 吸い込み蒸気とシリンダ壁との間の熱交換
- 蒸発器直後の連絡配管圧力損失
- 機械的摩擦損失動力
といった要因により理論断熱圧縮動力以上の圧縮動力を必要とします.つまり
\[
P = P_c + P_m
\]
- \(P\): 実際の圧縮機の駆動に必要な動力
- \(P_c\): 蒸気の圧縮に用いられる圧縮動力
- \(P_m\): 機械的摩擦損失動力の和
一般に機械効率 \(\displaystyle \frac{P_c}{P}\) は0.8~0.9 とされます.
ヒートポンプ
Definition 3 (ヒートポンプ)
冷媒を凝縮するために凝縮器で熱量 \(\Phi_k\) を放熱しているが,これを暖房やその他の加熱源として利用する装置をヒートポンプ装置と呼び,そのサイクルをヒートポンプサイクルという.
「冷媒の流れ方向自体は同じだが,吸熱と放熱の役割が冷凍機と逆になる.つまり,蒸発器で吸収した熱を暖房として利用するのがヒートポンプである」点に注意してください.
ヒートポンプサイクルの成績係数 \(COP_h\) は
\[
\begin{align}
COP_h
&= \frac{\Phi_k}{P}\\
&= \frac{\Phi_o + P}{P}\\
&= COP_c + 1
\end{align}
\]
この式より,ヒートポンプサイクルの成績係数は,同じ温度条件の冷凍サイクルの成績係数よりも1だけかならず大きい値になることがわかります.
製品としての能力
実際のエアコンなどの空調機器の「能力」は,単に冷媒回路が移動する熱量(冷却や加熱)だけでなく,室内ファンなどの補助的な消費電力の影響も加味して評価されることがあります
\[
\begin{align}
\text{冷房能力} &= \Phi_0 - \text{室内ファン消費電力}\\
\text{暖房能力} &= \Phi_k + \text{室内ファン消費電力}
\end{align}
\]
📘 理解度チェック問題
Exercise 1
容器に入った20℃の水8kgに,0℃の氷3.0kgを入れて放置した.容器は断熱されており,熱容量は無視できるとして,平衡状態の容器内の温度と容器内の氷の質量を求めよ.水の比熱を4.19kJ/(kg·K),氷の融解潜熱を334kJ/kgとする.
条件
| 水の質量 |
\(8.0 \, \text{kg}\) |
| 水の初温 |
\(20^\circ\text{C}\) |
| 氷の質量 |
\(3.0 \, \text{kg}\) |
| 氷の初温 |
\(0^\circ\text{C}\) |
| 水の比熱 |
\(4.19 \, \text{kJ/(kg·K)}\) |
| 氷の融解熱 |
\(334 \, \text{kJ/kg}\) |
水を0℃まで冷やすのに必要な熱量の計算
\[
\begin{align}
Q_{water}
&= (20 - 0) \text{K} \times 4.19 \text{kJ/kg·K} \times 8 \text{kg}\\
&= 670.4\text{kJ}
\end{align}
\]
氷が全て溶けるのに必要な熱量
\[
\begin{align}
Q_{ice}
&= 334\text{kJ/kg} \times 3.0\text{kg}\\
&= 1002\text{kJ}
\end{align}
\]
then, \(Q_{ice} > Q_{water}\) のため,氷がすべて溶け切ることはないことがわかります.
どれくらいの氷が残るのか?
水を0℃まで冷やすのに使用される氷の質量は
\[
\frac{Q_{water}}{\text{氷の融解熱}} = \frac{670.4\text{kJ}}{334\text{kJ/kg}} \approx 2.007\text{kg}
\]
したがって,平衡状態の容器内の温度と容器内の氷の質量は温度=0℃,氷の質量=0.993kgとなる.
Exercise 2
次の記述の内,正しいものを選べ
- 冷凍装置では,蒸発器で取り入れた熱と凝縮器で放出する熱量は等しい
- 蒸気圧縮冷凍装置の冷却能力は,圧縮機に加えるエネルギーに等しい
- 吸収冷凍装置の駆動源は熱であり,これを再生器に加えることにより低温を得る
- 蒸気圧縮ヒートポンプでは,装置内を循環する冷媒の流れ方向が冷凍サイクルのそれと逆方向になる
- 蒸気圧縮ヒートポンプの成績係数は,同じ温度条件での冷凍サイクルの成績係数より1だけ大きい.
- 冷凍サイクルの成績係数は,蒸発温度や凝縮温度には関係しない
- ヒートポンプの成績係数の値は常に1より大きい
- 冷凍装置における冷凍能力は,各機器への熱の出入り前後の比エンタルピーがわかれば計算できる
- 吸収冷凍機では,圧縮機を使用せずに,吸収器・発生器(再生器)・溶液ポンプなどを用いて冷媒を循環させ,冷熱を得る
- 蒸発温度と凝縮温度などの運転条件が同じでも,理論冷凍サイクルCOPに比べ,実際の装置におけるCOPは小さくなる
- 理論ヒートポンプサイクルでは,圧縮機で理論断熱圧縮動力を消費して,この圧縮動力に相当する熱と,蒸発器で取り入れた熱が冷媒に加わって凝縮負荷となり,凝縮器から放出される熱を利用する
Exercise 3 凝縮器について
次の記述の内,正しいものを選べ
- 理論凝縮負荷は冷凍能力に理論断熱圧縮動力を加えて求めることができる
Exercise 4 圧縮機について
次の記述の内,正しいものを選べ
- 二段圧縮冷凍装置は,一般に,低段圧縮機から出た冷媒ガスを一度冷却しているので,高段圧縮機の吐出しガスの温度が高くならないこと,また,圧縮機の損失を減らすことができ,圧縮機効率の低下を防ぐことができる.
- 理論断熱圧縮動力が同じ場合,圧縮機の全断熱効率が大きくなると,実際の圧縮機の駆動軸動力は小さくなる
- 圧縮機から吐出され,凝縮器に入る冷媒蒸気はかなり温度の高い過熱蒸気(高圧)
- 蒸発器をでて圧縮機に吸入される冷媒ガスは乾燥飽和蒸気より少し過熱された過熱蒸気(低圧)
Exercise 5
次の記述のうち,冷媒について正しいものを選べ
- 冷媒の蒸発潜熱は冷媒の種類関係なく一定である
- 同じ温度のもとでは,標準沸点の低い冷媒ほど圧力は高くなる
- 蒸気圧縮冷凍装置では,冷媒の蒸発の潜熱を利用して冷却作用を行う
- R 404A は共沸混合冷媒である
- 一般に,HFC冷媒は,HCFC冷媒と比べると誘電率が大きく,その電気絶縁性がやや劣る
- 一般に,アンモニア冷媒液は冷凍機油より比重が小さく,フルオロカーボン冷媒液は冷凍機油よりも比重が大きい
- フルオロカーボンの冷凍効果はアンモニアに比べ著しく大きいので,冷媒として広く用いられている
- アンモニアの標準沸点はR22の標準沸点より高い
- R134a冷媒は,塩素原子を含む
- 装置から漏洩した冷媒ガスは,フルオロカーボンの場合には床面近くに,アンモニアは天井近くに滞留しやすい
- 非共沸混合冷媒では,液と蒸気が共存する二相域において,液の組成と蒸気の組成は異なる
Exercise 6
冷凍能力 4.5 kWの冷凍装置があり,圧縮機の消費動力は 1.5 kWである.この装置の凝縮器で放出される熱量 [kW] はいくらか.また,この装置の冷凍サイクル成績係数はいくらか?
凝縮器で放出される熱量(凝縮負荷) \(\Phi_k\) は
\[
\Phi_k = 4.5 \text{kW} + 1.5 \text{kW}= 6 \text{kW}
\]
成績係数 \(COP_c\) は
\[
COP_c = \frac{4.5 \text{kW}}{1.5 \text{kW}} = 3
\]
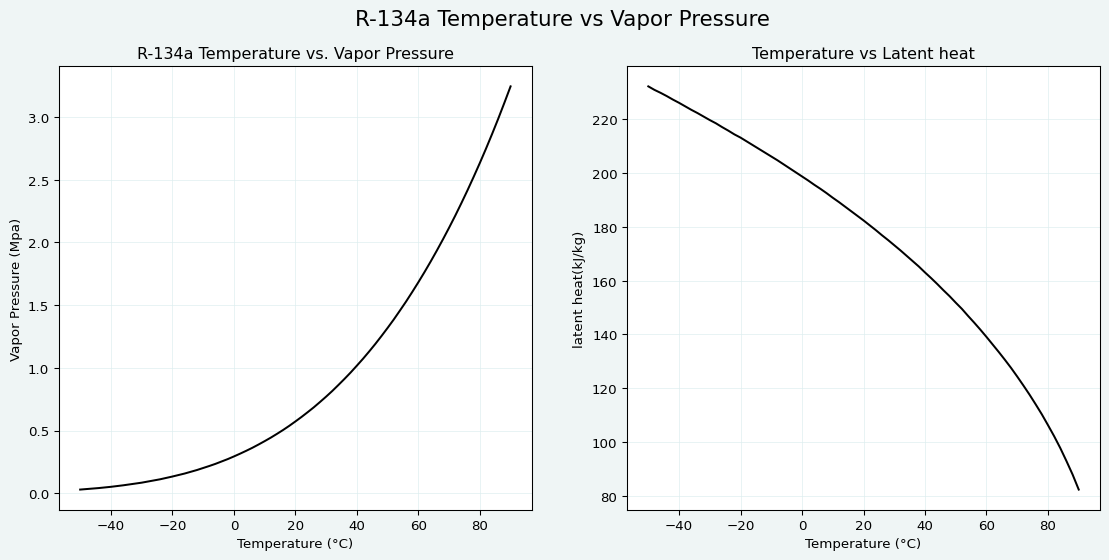
Appendix
数値目安
Code
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# read data
df = pd.read_csv("./r134_property.csv")
enthalpy = df['steam_enthalpy'] - df['liquid_enthalpy']
# plot temperature and pressure(mPa)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
# Set plot background color
fig.patch.set_facecolor('#EFF5F5')
fig.suptitle('R-134a Temperature vs Vapor Pressure', fontsize=16) # Overall title
ax1.plot(
df["temperature"], # X-axis: Vapor Pressure
df["Mpa"], # Y-axis: Temperature
color='black',
linestyle='solid', # Equivalent to 'dot' dash in Plotly
# marker='o', # Add markers
markersize=4, # Adjust marker size as desired
label='R-134a Vapor Pressure' # Optional: Add a label for legend
)
ax2.plot(
df["temperature"], # X-axis: Vapor Pressure
enthalpy, # Y-axis: kj/kg
color='black',
linestyle='solid', # Equivalent to 'dot' dash in Plotly
# marker='o', # Add markers
markersize=4, # Adjust marker size as desired
label='R-134a Vapor Pressure' # Optional: Add a label for legend
)
# Set axis 1 titles
ax1.set_title("R-134a Temperature vs. Vapor Pressure")
ax1.set_xlabel("Temperature (°C)")
ax1.set_ylabel("Vapor Pressure (Mpa)")
ax1.grid(True, which='both', color='#DDEEEF', linestyle='-', linewidth=0.5)
ax1.set_axisbelow(True)
# Set axis 2 titles
# ax2.set_yscale('log')
ax2.grid(True, which='both', color='#DDEEEF', linestyle='-', linewidth=0.5)
ax2.set_axisbelow(True)
ax2.set_xlabel("Temperature (°C)")
ax2.set_ylabel("latent heat(kJ/kg)") # Indicate log scale in label
ax2.set_title("Temperature vs Latent heat")
plt.show()
内部エネルギーとは?
Definition 4 内部エネルギー
物体の内部の分子運動による運動エネルギーと,分子間力によるポテンシャルエネルギーを,内部エネルギーと呼ぶ
内部エネルギーは,物体内部の分子の運動エネルギーと分子間力によるポテンシャルエネルギーから構成されます.運動エネルギーを \(E_k\), ポテンシャルエネルギーを \(E_p\) とすると
\[
\begin{align}
U
&= \sum_N(\text{分子の}E_k) + \sum_N(\text{分子間力による}E_p)\\
&= \sum_N\left(\frac{1}{2}mv^2 + \epsilon\right) + \sum_N(\text{分子間力による}E_p)\\
&= \sum_N\left(\frac{1}{2}m\overline{v}^2 + \epsilon\right) + \sum_N(\text{分子間力による}E_p)
\end{align}
\]
- \(\displaystyle\frac{1}{2}m\overline{v}^2\) は分子1個の並進運動(分子が回転しない運動)の平均運動エネルギー
- \(\epsilon\): 内部運動の運動エネルギー,H₂などの二原子分子やH₂O多原子分子の回転運動,または分子間距離の伸縮による振動運動