物質量と気体の体積

物質量

物質の量を表すときには，質量や体積を用いることが多いです．しかし，物質が化学変化するときには，物質を構成する原子，分子，イオンなどの粒子の結合の組み合わせが変化 します．そのため，化学で物質の量を表すときには，その中に含まれる粒子の「個数」で考えると便利になります．この粒子の個数に着目して表した物質の量を「物質量」といい，モル (mol) という単位で 表します．

定義 1 (アボガドロ定数)

原子や分子 1 mol あたりの粒子の数を示す次元をもつ物理量で

N_A = 6.0 × 10²³/mol

質量数 12 の炭素原子  ¹²C は 1.99 × 10⁻²³ g という決まった質量を持ちますがこのときの炭素原子の数は

$$ \frac{12\text{g}}{1.99 \times 10^{-23}} \approx 6.0 \times 10^{23} $$

計算でき，これをアボガドロ数といいます．アボガドロ数に mol⁻¹ の単位をつけたのがアボガドロ定数です．物質 1 molあたりの質量を モル質量 [g/mol] と呼びます．

例 1 (実験でアボガドロ定数を求める)

１円玉は1gのアルミニウムからできています．室温でのアルミニウム密度は2.7g/cm³なので体積は

$$ \text{1円玉体積} = \frac{1\text{g}}{2.7\text{g/cm}^3} = 1/2.7\text{cm}^3 $$

金属の固体では，金属の原子が規則正しく配列して金属結晶をつくっていて，結晶中の規則的な粒子の配列を結晶格子といいますその中に現れる最小の繰り返し単位を「単位格子」といい，アルミニウムは 面心立方格子の構造で，1 辺の長さが 4.04 × 10⁻⁸ cm の立方体（単位格子）中に原子が正味４個分，含まれています．

以上より

$$ N_A = \frac{\text{1円玉体積[cm]}^3}{\text{単位格子体積[cm]}^3} \times 4 \times \frac{\text{アルミニウムモル質量[g/mol]}}{\text{1円玉質量[g]}} $$

となるはずなので

import numpy as np

coin_volumn = np.float64(1 / 2.7)
grid_length = np.float64(4.04 * 10 ** (-8))
al_mol_mass = np.float64(27)

number_of_molecules = coin_volumn / (grid_length ** 3) * 4 * al_mol_mass

print(f"{{{number_of_molecules:.2e}}}")

{6.07e+23}

よってアボガドロ定数が計算できました．

---

定義 2 (アボガドロの法則)

同温・同圧で同体積の気体の中には，気体の種類によらず，同数の分子が含まれる．

実測によると [0℃, 1.013 × 10⁵ Pa] において，多くの気体 1 mol の体積は 22.4 Lになります． この物質 1 molあたりの体積をモル体積と呼び，標準気圧での気体のモル体積は 22.4L/mol になります．

気体の物質量はこの関係式を用いると以下のように求めることができます

$$ \text{気体の物質量[mol]} = \frac{\text{標準状態での気体の体積[L]}}{22.4 \text{L/mol}} $$

例 2 (二酸化炭素の体積を求める)

二酸化炭素の個体である「ドライアイス」が11g与えられているとき，これを [0℃, 1.013 × 10⁵ Pa] のもとで気化させたときの二酸化炭素の体積を求めてみます．

まず二酸化炭素 CO₂ は 44g/mol = 12 + 2 × 16 とします．

元素名	元素記号	原子番号	原子量
炭素	C	6	12.0107
酸素	O	8	15.9994

11.0gのドライアイスの物質量は

$$ \frac{11.0\text{g}}{44 \text{g/mol}} = 0.25\text{mol} $$

アボガドロの法則より， [0℃, 1.013 × 10⁵ Pa] において，気体 1 mol の体積は 22.4 Lになるので，気化した二酸化炭素の体積は

22.4L/mol × 0.25mol = 5.6L

と推定することができます．室温（約23℃）でドライアイスを昇華させたとき，1 mol の二酸化炭素が占める体積は 22.4 L にはなりません．直感的イメージとして， ボイル・シャルルの法則より同じ気体のもとでは温度と体積は比例するので，もうすこし大きい体積となります．

---

例 3 (一般気体定数)

1 molの気体は，アボガドロの法則より，気体の種類関係なく同温・同圧で同体積の気体の中に同数の分子が含まれます．ボイル=シャルルの法則という理想気体の性質に関する経験法則，及び 0 ^∘C, 1気圧(1.013 × 10⁵ [Pa]) の標準状態では22.4Lの体積の中に含まれることから気体定数を以下のように計算できます

$$ \begin{align} R_0 &= \frac{pv}{T}\\ &= \frac{1.013 \times 10^5 \times 22.4}{273 \times 10^3}\\ &= 8.31 \text{[J/mol}\cdot\text{K]} \end{align} $$

これを n モルの理想気体に当てはめると

pv = nR₀T

という理想気体の状態方程式を得ます．

---

気体の密度と分子量

密度は単位体積あたりの質量を表した物理量で，固体・液体の密度は [g/cm3]，気体の密度は体積１ L あたりの質量 [g/L] の単位で表します． つまり，気体 1L あたりの質量を「気体の密度」になります．

ノートシャボン玉でガス缶の中身を調べる

• 水素 H₂, 酸素 O₂, 二酸化炭素 CO₂ がそれぞれ充填された３つのガス缶がある
• どの缶にどの気体が入っているのかわからない

このとき，どの缶にどの気体が入っているか知りたいとします．調べる一つの方法として，各気体で同じ大きさくらいに膨らませたシャボン玉をつくり密度を比較する方法が有ります． 標準状態における気体の密度は

$$ \frac{\text{分子量[g]}}{22.4\text{L/mol}} $$

で計算できるので，

$$ \begin{align} \text{H}_2\text{の密度} &= \frac{2.0}{22.4} \approx 0.089\text{g/L}\\ \text{O}_2\text{の密度} &= \frac{32}{22.4} \approx 1.4\text{g/L}\\ \text{CO}_2\text{の密度} &= \frac{44}{22.4} \approx 2.0\text{g/L} \end{align} $$

密度が重いほど，同じ環境下では下降速度は速くなることから．同程度の大きさのシャボン玉で下降するとき速さを比較すれば，どの缶にどんな気体が入っているのか推測することができます．

なお，空気の平均分子量は，空気の組成を N₂ : O₂ = 4 : 1 とすると

空気の平均分子量 = 28 × 0.8 + 32 × 0.2 = 28.8g/mol

となることから，各期待の密度を計算するまでもなく，水素が入ったシャボン玉は上昇し，酸素が入ったシャボン玉は比較的ゆっくり下降，二酸化炭素が入ったシャボン玉は酸素のシャボン玉より速く下降するとわかります．

気体の内部エネルギーとモル比熱

気体の内部エネルギーを，温度 T と体積 V を独立変数として，U = U(T, V) と表すと

$$ \operatorname{grad} U \equiv \left(\left(\frac{\partial U}{\partial T}\right)_V, \left(\frac{\partial U}{\partial V}\right)_T\right) $$

これをもちいて整理すると

$$ dU = \left(\frac{\partial U}{\partial T}\right)_VdT + \left(\frac{\partial U}{\partial V}\right)_TdV $$

熱力学第一法則より 気体が外部になす微小仕事 dW = PdV より

$$ dQ = \left(\frac{\partial U}{\partial T}\right)_VdT + \left[ \left(\frac{\partial U}{\partial V}\right)_T + P\right]dV \label{temp-vol-eq} $$

定積モル比熱と定圧モル比熱

体積一定の容器に入れた気体に熱を加える場合を考えます． で dV = 0 とおけるので

$$ dQ = \left(\frac{\partial U}{\partial T}\right)_VdT $$

ここから体積一定のもとで，気体の温度を単位温度上げるのに必要な熱量は

$$ \frac{dQ}{dT} = \left(\frac{\partial U}{\partial T}\right)_V $$

これをモル数 n で割ると定積モル比熱になります．

定義 3 定積モル比熱

定積モル比熱 C_v [J/mol･K] は以下のように定義される

$$ C_v = \frac{1}{n} \left(\frac{\partial Q}{\partial T}\right)_V = \frac{1}{n} \left(\frac{\partial U}{\partial T}\right)_V $$

圧力一定の条件下で1モルあたりの物質の温度を 1 K 上げるのに必要な熱量を考えます．これは定圧モル比熱 C_p と呼び，

$$ C_p = C_v + \left[ \left(\frac{\partial U}{\partial V}\right)_T + P\right]\frac{1}{n}\left(\frac{\partial V}{\partial T}\right)_P $$

マイヤーの関係式

単原子分子理想気体では状態方程式

$$ \frac{PV}{T} = nR $$

が成立するので

$$ \left(\frac{\partial V}{\partial T}\right)_P = n\frac{R}{P} $$

また，内部エネルギーも

$$ U = \frac{3}{2}nRT $$

であるので $\displaystyle \left(\frac{\partial U}{\partial V}\right)_T = 0$ より

C_p = C_v + R

というマイヤーの関係式が得られます．

📘 理解度チェック

練習 1 センター2016物理追試第５問「ぶら下がるシリンダーと熱力学第１法則」

1. シリンダーが (a) の状態で静止しているとき，P を P₀, M, g, S の関数として表せ
2. シリンダー内の気体を温めると，シリンダーはゆっくり下降し，(b) の状態で静止した．このとき，体積の変化 ΔV と 内部エネルギー ΔU は ΔT の関数としてどのように表せるか？

ノートSolution

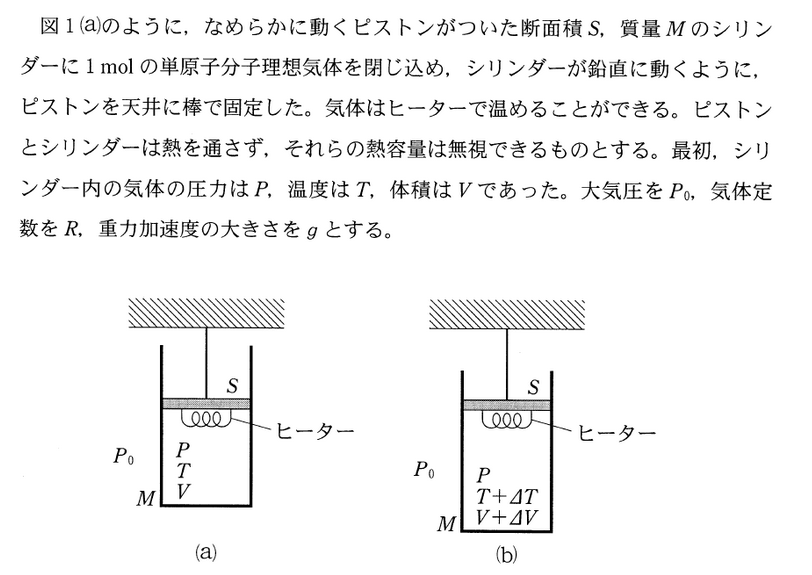
1. シリンダーが (a) の状態で静止しているとき，P を P₀, M, g, S の関数として表せ

下向きの力の一つとして

質量 × 加速度 = 力

よって, Mg という力が下向きに働いています． また，シリンダー内部の圧力 P も下向きの力として働くので

下向きの力 = S × P + Mg

上向きの力として，P₀ × S があり，初期状態では静止している = 上向きと下向きの力が均衡しているので

S × P + Mg = S × P₀

したがって，

$$ P = P_0 = \frac{Mg}{S} $$

2. シリンダー内の気体を温めると，シリンダーはゆっくり下降し，(b) の状態で静止した．このとき，体積の変化 ΔV と 内部エネルギー ΔU は ΔT の関数としてどのように表せるか？

単原子分子理想気体では内部エネルギーは

$$ U = \frac{3}{2}RT $$

したがって

$$ \Delta U = \frac{3}{2}R\Delta T $$

また，状態変化後も圧力は P で同じなので，理想気体の状態方程式より

$$ \frac{V}{T} = \frac{V + \Delta V}{T + \Delta T} $$

したがって，

$$ \Delta V = \frac{V}{T}\Delta T $$

練習 2 運動エネルギーと温度と圧力

密閉された炉に一箇所小さな孔が空いている．

• 孔の厚さは0
• 炉外の空気は温度が0℃で圧力は100kPa
• 炉内の空気は温度調整して57℃で一定
• 空気は理想気体とする

十分時間が経った後は圧力が一定になるとして，この定常的な状態での炉内の圧力を求めよ．

ただし，分子の自乗平均速度は平均速度の自乗と一致するとする．

ノートSolution

炉内を1，炉外を2とすると，平衡状態では炉外へ出る分子と炉外から入る分子の数が等しいはずなので，

Av₁N₁t = Av₂N₂t

• v_i 分子の平均速度
• A: 孔の断面積
• N_i: 個数密度
• t: 単位時間

理想気体においては

$$ \frac{3}{2}k_BT = \frac{1}{2}m\overline{v^2} $$

と温度は自乗平均速度に比例する．また理想気体の状態方程式より，個数密度は圧力 P に比例し，温度 T に反比例するので

$$ \begin{align} \frac{v_1}{v_2} &= \sqrt{\frac{T_1}{T_2}}\\ \frac{N_1}{N_2} &= \frac{P_1}{P_2}\frac{T_2}{T_1} \end{align} $$

したがって，

$$ \begin{align} p_1 &= p_2\sqrt{\frac{T_1}{T_2}}\\ &= 100\text{kPa} \times \sqrt{\frac{330.15}{273.15}}\\ &\approx 110\text{kPa} \end{align} $$