import CoolProp.CoolProp as CP
fluid = "R22"
# 温度設定(すべて [K] に変換)
T_evap = -15 + 273.15 # 蒸発温度
T_cond = 30 + 273.15 # 凝縮温度
dT_subcool = 5 # 過冷却
dT_superheat = 5 # 過熱
# 飽和圧力(蒸発器側と凝縮器側)
P_evap = CP.PropsSI(
"P", "T", T_evap, "Q", 1, fluid
) # 温度 T_evap で品質(乾き度)Q = 1 のとき(=飽和蒸気)の圧力 P
P_cond = CP.PropsSI(
"P", "T", T_cond, "Q", 0, fluid
) # 温度 T_cond で品質(乾き度)Q = 0 のときの圧力 P
# 状態1: 蒸発器出口(過熱蒸気)
T1 = T_evap + dT_superheat
h1 = CP.PropsSI("H", "T", T1, "P", P_evap, fluid)
s1 = CP.PropsSI("S", "T", T1, "P", P_evap, fluid)
# 状態2: 圧縮機出口(断熱圧縮)
h2 = CP.PropsSI("H", "P", P_cond, "S", s1, fluid)
T2 = CP.PropsSI("T", "P", P_cond, "H", h2, fluid)
# ========= 等エントロピー線を生成 =========
# 入口圧~出口圧まで対数刻みでサンプリング
P_line = np.logspace(np.log10(P_evap), np.log10(P_cond), 200) # [Pa]
h_line = CP.PropsSI("H", "P", P_line, "S", s1, fluid) # [J/kg]
# 状態3: 凝縮器出口(過冷却液)
T3 = T_cond - dT_subcool
h3 = CP.PropsSI("H", "T", T3, "P", P_cond, fluid)
# 状態4: 膨張弁出口(等エンタルピー膨張)
h4 = h3
T4 = CP.PropsSI("T", "P", P_evap, "H", h4, fluid)
# 冷凍能力(1 kgあたり)
q_in = h1 - h4 # 蒸発器での吸熱
w_in = h2 - h1 # 圧縮機の仕事
q_out = h2 - h3 # 凝縮器での放熱
COP = q_in / w_in # 成績係数
# 結果表示
print("=== 冷凍サイクル各点の状態(単位: SI) ===")
print(f"状態1(過熱蒸気): T={T1 - 273.15:.2f}°C, h={h1 / 1000:.2f} kJ/kg")
print(f"状態2(圧縮後) : T={T2 - 273.15:.2f}°C, h={h2 / 1000:.2f} kJ/kg")
print(f"状態3(過冷却液): T={T3 - 273.15:.2f}°C, h={h3 / 1000:.2f} kJ/kg")
print(f"状態4(膨張後) : T={T4 - 273.15:.2f}°C, h={h4 / 1000:.2f} kJ/kg")
print("\n=== 性能指標 ===")
print(f"冷凍能力 q_in : {q_in / 1000:.2f} kJ/kg")
print(f"圧縮機仕事 w_in : {w_in / 1000:.2f} kJ/kg")
print(f"COP (成績係数) : {COP:.2f}")
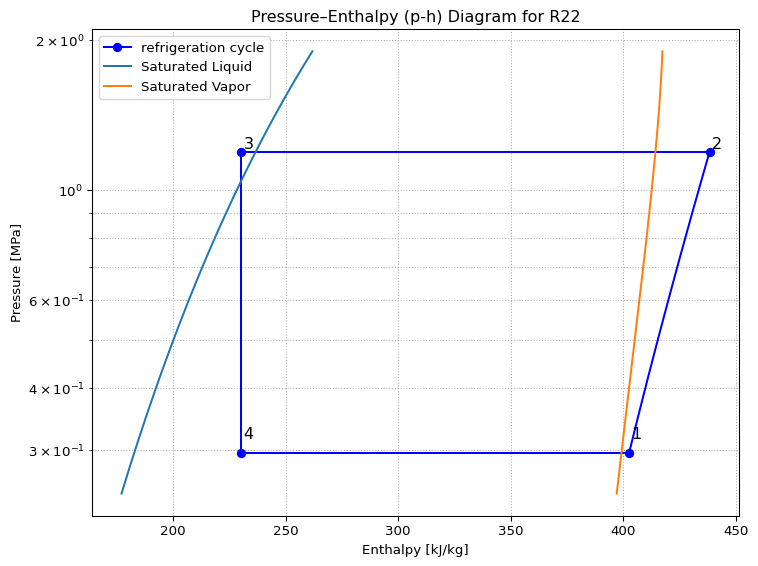
# plot
h_points = [h2 / 1e3, h3 / 1e3, h4 / 1e3, h1 / 1e3]
P_points = [P_cond / 1e6, P_cond / 1e6, P_evap / 1e6, P_evap / 1e6]
plt.figure(figsize=(8, 6))
plt.plot(
h_points,
P_points,
marker="o",
linestyle="-",
color="blue",
label="refrigeration cycle",
)
# Add labels at each point
for i, (h, P) in enumerate(zip(h_points, P_points), start=1):
plt.text(
h + 1, P + 0.02, f"{(i % 4) + 1}", fontsize=12, color="black"
) # adjust offsets as needed
plt.plot(h_line / 1000, P_line / 1e6, linestyle="-", color="blue")
plt.xlabel("h [kJ/kg]")
plt.ylabel("P [MPa]")
plt.grid(True)
# Saturation curve
T_min = -20 + 273.15
T_crit = 49 + 273.15 # [K]
T_sat = np.linspace(T_min, T_crit - 1e-5, 200)
p_sat = PropsSI("P", "T", T_sat, "Q", 0, fluid)
h_liq = PropsSI("H", "T", T_sat, "Q", 0, fluid) / 1000 # [kJ/kg]
h_vap = PropsSI("H", "T", T_sat, "Q", 1, fluid) / 1000 # [kJ/kg]
plt.plot(h_liq, p_sat / pa_converter, label="Saturated Liquid")
plt.plot(h_vap, p_sat / pa_converter, label="Saturated Vapor")
plt.yscale("log")
plt.xlabel("Enthalpy [kJ/kg]")
plt.ylabel("Pressure [MPa]")
plt.title(f"Pressure–Enthalpy (p-h) Diagram for {fluid}")
plt.legend()
plt.grid(True, which="both", ls=":")
plt.tight_layout()
plt.show()