上極限集合と下極限集合
Definition 1 集合列
集合 \(\Gamma\) が \(\mathbb N\) のとき,集合族 \(\{A_\gamma\}_{\gamma\in \Gamma}\) は
\[
\{A_1, A_2, \cdots, A_n, \cdots \}
\]
と表される.これを集合列という.
集合列の和集合・直和・共通部分
\[
\begin{align}
\text{集合列の和集合:} \ \ & \bigcup_{n=1}^\infty A_n\\
\text{集合列の直和:} \ \ & \bigsqcup_{n=1}^\infty A_n\\
\text{集合列の共通部分:} \ \ & \bigcap_{n=1}^\infty A_n
\end{align}
\]
Definition 2 上極限集合
\[
\lim_{n\to\infty}\sup A_n = \bigcap_{n=1}^\infty\bigcup_{k=n}^\infty A_k
\]
\(x\in \bigcap_{n=1}^\infty\bigcup_{k=n}^\infty A_k\) をまず考えます.これはすべての \(n\) に対して
\[
x \in \bigcup_{k=n}^\infty A_k
\]
を意味します.一方,\(x \in \bigcup_{k=n}^\infty A_k\) は \(k\geq n\) を満たすある \(k\) に対して
\[
x\in A_k
\]
これらふたつをあわせると
\[
\bigcap_{n=1}^\infty\bigcup_{k=n}^\infty A_k = \{x | \text{すべての n に対して,ある} k\geq n \text{が存在して} x \in A_k\}
\]
上極限集合を無限に多くの \(k\) に対して \(x\in A_k\) と解釈する
\(x\in\lim\sup A_n\) のとき,ある \(k_1\) に対して \(x \in A_{k_1}\) となります.ここで
\[
\bigcap_{n=1}^\infty\bigcup_{k=n}^\infty A_k = \left(\bigcap_{n=1}^{k_1}\bigcup_{k=n}^{\infty} A_k\right) \bigcap \left(\bigcap_{n>k_1}^\infty\bigcup_{k=n}^\infty\right)
\]
であることから,\(k\geq k_1 + 1\) をみたすある \(k_2\) についても
\[
x \in A_{k_2}
\]
とならなくてはいけません.これを繰り返していくと \(k_1 < k_2< \cdots < k_n < \cdots\) で
\[
x \in A_{k_1}, x \in A_{k_2}, \cdots, x \in A_{k_n}, \cdots
\]
つまり,\(x\in\lim\sup A_n\) であるならば,無限に多くの \(k\) に対して \(x\in A_k\) ということになります.
逆に,「無限に多くの \(k\) に対して \(x\in A_k\)」であるならば,
\[
\text{任意の $n$ について $k\geq n$ を満たす} \ \ x\in A_{k} \ \ \text{となるような $k$ が存在する}
\]
であるので,
\[
\bigcap_{n=1}^\infty\bigcup_{k=n}^\infty A_k = \{x | \text{すべての n に対して,ある} k\geq n \text{が存在して} x \in A_k\}
\]
が成立します.
Definition 3 下極限集合
\[
\lim_{n\to\infty}\inf A_n = \bigcup_{n=1}^\infty\bigcap_{k=n}^\infty A_k
\]
下極限集合は,
\[
\lim_{n\to\infty}\inf A_n = \{x | \text{ある $n$ が存在して,$k\geq n$ となるようなすべての $k$ について $x \in A_k$}\}
\]
と解釈できます
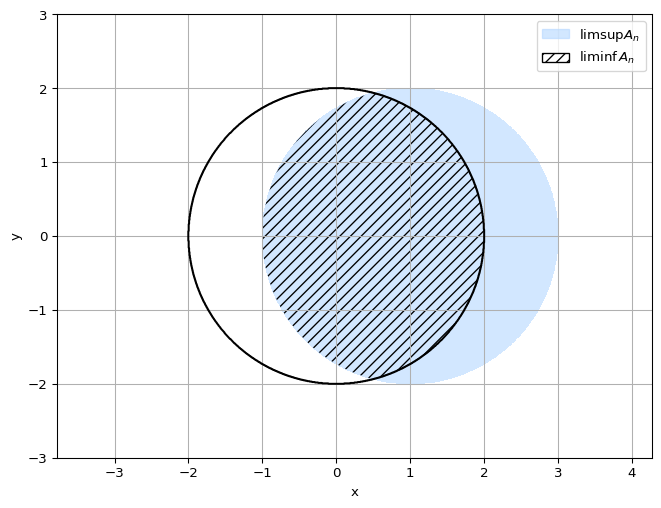
Example 1 supとinfの関係
\(i \in \mathbb N\) として,集合 \(A_i\) を以下のように定義します
\[
A_i = \left\{(x, y) | t_i = 1 - \frac{1}{i}, (x - t_i)^2 + y^2 < 4\right\}
\]
このとき,
\[
\begin{align}
\lim_{n\to\infty} \sup A_n &= \text{青の境界を含まない開集合}\\
\lim_{n\to\infty} \inf A_n &= \text{黒斜線部のの境界を含まない開集合}
\end{align}
\]
また,
\[
\lim_{n\to\infty} \inf A_n \subseteq \lim_{n\to\infty} \sup A_n
\]
であることがわかります.
Code
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
x = np.linspace(-2.5, 3, 1000)
y = np.linspace(-3, 3, 1000)
X, Y = np.meshgrid(x, y)
# Intersection region
region1 = (X - 1)**2 + Y**2 <= 4
region2 = X**2 + Y**2 <= 4
intersection_common = region1 & region2
# Plot
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, region1, levels=[0.5, 1], colors='#B4D7FF', alpha=0.6)
plt.contour(X, Y, region2, levels=[0.5], colors='black')
plt.contourf(X, Y, region1, levels=[0.5, 1], colors='none', hatches=['///'])
# 凡例用パッチ作成
patch_region_sup = mpatches.Patch(color='#B4D7FF', alpha=0.6, label='$\lim\sup A_n$')
patch_region_inf = mpatches.Patch(facecolor='white', hatch='///', label='$\lim\inf A_n$', edgecolor='black')
plt.legend(handles=[patch_region_sup, patch_region_inf])
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.grid(True)
plt.show()
事象列の上極限集合と下極限集合
\((\Omega, \mathcal{F}, P)\) を確率空間とします.事象の列 \(A_n \in \mathcal{F}\) があったとして,
\[
\lim_{n\to\infty}\sup A_n
\]
を考えてみます.
\[
\omega \in \lim_{n\to\infty}\sup A_n = \bigcap_{k=1}^\infty\bigcup_{n=k}^\infty A_n
\]
とすれば,\(\omega\) は どんなに大きな\(k\) をとってもそれ以降の \(A_n\) に必ず含まれることを意味しています.もし \(\omega\) が有限個の \(\{A_{n_1}, \cdots, A_{n_m}\}\) にのみ属するならば矛盾してしまうので,無限個の \(A_n\) に属していなくてはならないことになります.つまり,
- \(\mathbb P(\lim\sup A_n)\) は「\(\omega \in A_k\) を満たすような事象が,たびたび,しかし何回でも起こる確率」と解釈できます
次に,
\[
\lim_{n\to\infty}\inf A_n
\]
これは,ある \(n\) 以降全ての \(k\geq n\) で \(\omega \in A_k\) となっているので,
- 「十分先では常に \(A_k\) が起こっているという事象」を意味します.
\(\mathbb P(\lim\sup A_n)\) は「\(\omega \in A_k\) を満たすような事象が,たびたび,しかし何回でも起こる確率」と解釈できることから
\[
P(A_k\ , \ \text{i.o.})
\]
と表記する場合もあります.i.o. は infinitely oftenの略です.