P-valueの定義
Definition 1 P value
データにばらつきがある場合,ばらつきだけの原因で評価指標が観測された以上の大きな値を取る確率
P値はNHSTの文脈で用いられる指標です.統計的文脈に則した定義を与えるとすると,
\(H_o: \theta \in \Theta_0\) vs \(H_o: \theta \notin \Theta_0\) なるNHSTにおいて,棄却域が
\[
R = \{\pmb x | W(\pmb x) > c\}
\]
で与えられる検定を考えます.このとき
\[
p(\pmb x) = \sup_{\theta \in \Theta_0} P_\theta (W(\pmb X) \geq W(\pmb x))
\]
をP値もしくは有意確率といいます.
Theorem 1 Type I エラーのバウンド
すべての \(\theta \in \Theta_0\) とすべての \(\alpha \in (0, 1)\) について
\[
P_\theta(p(\pmb X) \leq \alpha) \leq \alpha
\]
が成り立つ.
\(\theta \in \Theta_0\) を任意に固定して
\[
p(\pmb x | \theta) = P_\theta(W(\pmb X) \geq W(\pmb x))
\]
とおきます.\(-W(\pmb X)\) の分布関数を \(F_\theta(w)\) とすると
\[
\begin{align}
p(\pmb x | \theta)
&= P_\theta(-W(\pmb X) \leq -W(\pmb x))\\[5pt]
&= F_\theta(-W(\pmb x))
\end{align}
\]
\(F_\theta(-W(\pmb X))\) は分布関数 \(F_\theta\) に \(-W(\pmb X)\) を代入したものなので,\((0, 1)\) 上に一様分布します. したがって,確率測度 \(P_\theta\) に対して
\[
P_\theta(p(\pmb X | \theta) \leq \alpha) = P_\theta(F_\theta(-W(\pmb X))\leq \alpha) = \alpha
\]
定義より
\[
p(\pmb x) = \sup_{\theta^\prime \in \Theta_0} p(\pmb x | \theta^\prime) \geq p(\pmb x | \theta)
\]
であるので
\[
P_\theta(p(\pmb X) \leq \alpha) \leq P_\theta(p(\pmb X | \theta) \leq \alpha) = \alpha
\]
この定理は,帰無仮説が真であるとき,p値が \(\alpha\) 以下となる確率(=Type I error rate)は高々 \(\alpha\) であることを保証しています.
わかりやすいイメージとして,指示関数 \(\mathbf{1}\{p(\pmb X) \leq \alpha\}\) を考えます.この関数は
- p値が \(\alpha\) 以下のとき \(1\)(帰無仮説を棄却)
- p値が \(\alpha\) より大きいとき \(0\)(帰無仮説を棄却しない)
を返します.帰無仮説が真のもとで繰り返しサンプリングを行い,この指示関数の値を記録すると,その平均(=棄却する割合)は
\[
E_\theta[\mathbf{1}\{p(\pmb X) \leq \alpha\}] = P_\theta(p(\pmb X) \leq \alpha) \leq \alpha
\]
となります.つまり,帰無仮説が真であるにもかかわらず誤って棄却してしまう割合は,長期的に見て \(\alpha\) 以下に抑えられるということです.
Example 1
\(X_1, \cdots. X_n \overset{\mathrm{iid}}{\sim} N(\mu, \sigma^2_0)\) とし,\(\sigma^2_0\) は既知であるとする.
- \(H_0: \mu = \mu_0\)
- \(H_1: \mu =\neq \mu_0\)
となる両側検定については,検定統計量は
\[
W(\bar X) = \sqrt{n}|\bar X - \mu_0|/\sigma_0
\]
となり,有意水準 \(\alpha\) について,対応する棄却域は
\[
R = \{\bar x | W(\bar x) > z_{\alpha/2}\}
\]
このとき,\(Z = \sqrt{n}(\bar X - \mu_0)/\sigma_0\) とおくと,\(W(\bar X) = |Z|\) になります.また,\(H_0\) のもとで \(Z \sim N(0, 1)\) であるので
\[
\begin{align}
p(\bar x)
&= P_{\mu_0}(W(\bar X) \geq W(\bar x))\\
&= P(|Z| \geq \sqrt{n}|\bar x - \mu|/\sigma_0)
\end{align}
\]
\(\bar x \in R\) のときは
\[
\begin{align}
p(\bar x)
&= P(|Z| \geq \sqrt{n}|\bar x - \mu_0|/\sigma_0)\\
&\leq P(|Z| \geq z_{\alpha/2}) = \alpha
\end{align}
\]
したがって,定理 Theorem 1 より
\[
P_{\mu_0}(p(\bar X) \leq \alpha) = \alpha
\]
となります.仮にデータを観測して \(p(\bar x) < 0.01\) となるとき.\(H_0\) のもとで,P値が0.01より小さくなる確率は 0.01 より小さいことがわかります.
統計的判定とドメイン領域判定
医薬品の臨床試験においては、\(\text{p-value}<\alpha\) のとき「統計的に有意である」と判定し,帰無仮説(処置効果が存在しない)を棄却する,というプロトコルが用いられます.
しかし,この判定はあくまで統計的判定であり,医学的に意味のある処置効果が存在することを直接示すものではないです.P値はあくまで,
- データにばらつきがある場合,ばらつきだけの原因で評価指標が観測された以上の大きな値を取る確率
を表す量であり,
\[
P_\theta(p(\pmb X) \leq \alpha) \leq \alpha \, \ (\theta \in \Theta_0)
\]
を用いたNeyman-Pearson流の意思決定フレームワークにおけるType I Error制御にすぎません.「医薬品の効果があった」という医学的判定とは異なります. 医学的判定において重要なのは,
- 効果量の大きさが臨床的に意味のある水準か
- 副作用や安全性とのバランスは妥当か
- 除外すべき患者がデータに含まれていないか?
といったP-valueの枠外の観点と照らし合わせて,結果を解釈して意思決定を行うことです.
統計的判定が得られなければ,医学的判断の対象にはなりえない,といったプロトコルを事前に作成して統計的判定の指標としてP値を用いるのはよいですが, P値そのものは医学的有効性や臨床的価値の判断とは切り分けて解釈されるべきです.
p-valueをベイズ的に考える
p-value を用いた統計的判定では、対立仮説 \(H_1\) が成立すると結論づけるために,まず帰無仮説 \(H_0\) を設定し,そのもとで観測データがどの程度「起こりにくいか」を評価する、という手続きを取ります.
ここで,p-valueをベイズ的な観点で考えてみます. データ確認前に持っている仮説に対する信念を事前確率 \(P(H_0), P(H_1)\) として表すとして,
\[
R = \frac{P(H_1)}{P(H_0)}
\]
という事前オッズを考えることができます.これはデータを観測する前の段階で,どちらの仮説を支持するかを表す量となります
\[
R \geq 1
\]
であるならば,\(H_0\) よりも \(H_1\) のほうが起こりやすいと想定していることになります.
\[
\left\{
\begin{array}{c}
H_0: \Delta \leq 0\\
H_1: \Delta > 0\\
\end{array}\right.
\]
および検定統計量を \(T\), データから計算される \(T\) の値を \(t_0\) とする検定をおこなったとき,p-valueは定義より
\[
\text{p-value} = Pr(T \geq t_0 | H_0)
\]
ここでベイズの定理を用いると
\[
\begin{align}
\operatorname{Pr}\left(H_1 \mid T \geq t_0\right) &
=\frac{\operatorname{Pr}\left(H_1, T \geq t_0\right)}{\operatorname{Pr}\left(T \geq t_0\right)} \\
& =\frac{\operatorname{Pr}\left(T \geq t_0 \mid H_1\right) \operatorname{Pr}\left(H_1\right)}{\operatorname{Pr}\left(T \geq t_0|H_0\right) \operatorname{P}\left(H_0\right) + \operatorname{Pr}\left(T \geq t_0|H_1\right) \operatorname{P}\left(H_1\right)}\\
&= \frac{\operatorname{Pr}\left(T \geq t_0 \mid H_1\right) R}{\operatorname{Pr}\left(T \geq t_0|H_0\right) + \operatorname{Pr}\left(T \geq t_0|H_1\right) R}\\
&= \frac{\operatorname{Pr}\left(T \geq t_0 \mid H_1\right) R}{\text{p-value} + \operatorname{Pr}\left(T \geq t_0|H_1\right) R}
\end{align}
\]
\(\operatorname{Pr}(T\geq t_0 | H_1)\) は検出力に対応することを考えると,
\[
\operatorname{Pr}\left(H_1 \mid T \geq t_0\right) = \frac{\text{power} \times R}{\text{p-value} + \text{power} \times R}
\]
シミュレーション: 検出力・p-value・事前オッズと事後確率の関係
検出力(power),p-value,事前オッズ \(R\) を動かしたときの \(\Pr(H_1 | T \geq t_0)\) を計算してみます.
テーブル表示
import pandas as pd
import numpy as np
def posterior_prob(power, p_value, R):
"""Pr(H1 | T >= t0) を計算"""
return (power * R) / (p_value + power * R)
# パラメータの組み合わせ
Rs = [0.5, 1.0, 2.0]
powers = [0.05, 0.1, 0.2, 0.4, 0.6, 0.8]
p_values = [0.001, 0.01, 0.05, 0.1]
# マルチインデックステーブル作成
index = pd.MultiIndex.from_product([Rs, powers], names=["R", "Power"])
df = pd.DataFrame(index=index, columns=[f"{p}" for p in p_values])
for R in Rs:
for power in powers:
for p in p_values:
df.loc[(R, power), f"{p}"] = posterior_prob(power, p, R)
df.columns.name = "p-value"
df = df.astype(float).round(3)
df
| R |
Power |
|
|
|
|
| 0.5 |
0.05 |
0.962 |
0.714 |
0.333 |
0.200 |
| 0.10 |
0.980 |
0.833 |
0.500 |
0.333 |
| 0.20 |
0.990 |
0.909 |
0.667 |
0.500 |
| 0.40 |
0.995 |
0.952 |
0.800 |
0.667 |
| 0.60 |
0.997 |
0.968 |
0.857 |
0.750 |
| 0.80 |
0.998 |
0.976 |
0.889 |
0.800 |
| 1.0 |
0.05 |
0.980 |
0.833 |
0.500 |
0.333 |
| 0.10 |
0.990 |
0.909 |
0.667 |
0.500 |
| 0.20 |
0.995 |
0.952 |
0.800 |
0.667 |
| 0.40 |
0.998 |
0.976 |
0.889 |
0.800 |
| 0.60 |
0.998 |
0.984 |
0.923 |
0.857 |
| 0.80 |
0.999 |
0.988 |
0.941 |
0.889 |
| 2.0 |
0.05 |
0.990 |
0.909 |
0.667 |
0.500 |
| 0.10 |
0.995 |
0.952 |
0.800 |
0.667 |
| 0.20 |
0.998 |
0.976 |
0.889 |
0.800 |
| 0.40 |
0.999 |
0.988 |
0.941 |
0.889 |
| 0.60 |
0.999 |
0.992 |
0.960 |
0.923 |
| 0.80 |
0.999 |
0.994 |
0.970 |
0.941 |
上記テーブルから以下のことがわかります:
- p-value が小さいほど:\(\Pr(H_1 | T \geq t_0)\) は大きくなる
- 検出力が高いほど:\(\Pr(H_1 | T \geq t_0)\) は大きくなる
- 事前オッズ \(R\) が大きいほど:\(\Pr(H_1 | T \geq t_0)\) は大きくなる
特に,検出力が低い場合(power = 0.05)では,\(R = 1\), p-value が 0.05 であっても事後確率は約 50% にとどまり,\(H_1\) が正しいとは言い難い状況になります.
シミュレーション: One-sample t検定と p-value の分布
ガンマ分布からサンプルを生成して one-sample t 検定を行います.
- \(H_0: \mu = 0\)
- \(H_1: \mu \neq 0\)
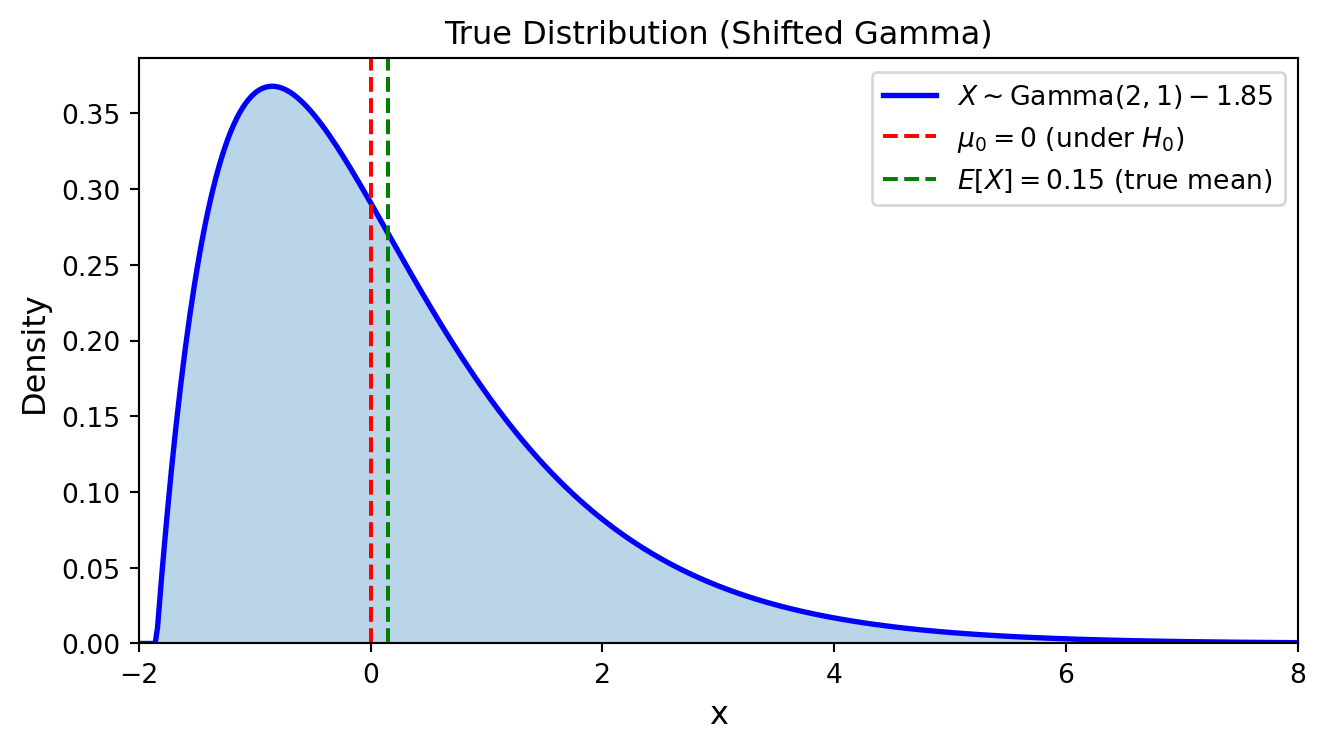
真の分布として \(X \sim \text{Gamma}(2, 1) - 1.85\) を仮定します(\(E[X] = 0.15 > 0\),右に歪んだ分布).
真の分布
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# シフトしたガンマ分布の確率密度関数
x = np.linspace(-2, 8, 500)
shift = 1.85
pdf = stats.gamma.pdf(x + shift, a=2, scale=1)
fig, ax = plt.subplots(figsize=(7, 4))
ax.plot(x, pdf, 'b-', lw=2, label=r'$X \sim \mathrm{Gamma}(2, 1) - 1.85$')
ax.fill_between(x, pdf, alpha=0.3)
ax.axvline(x=0, color='red', linestyle='--', lw=1.5, label=r'$\mu_0 = 0$ (under $H_0$)')
ax.axvline(x=0.15, color='green', linestyle='--', lw=1.5, label=r'$E[X] = 0.15$ (true mean)')
ax.set_xlabel('x', fontsize=12)
ax.set_ylabel('Density', fontsize=12)
ax.set_title('True Distribution (Shifted Gamma)', fontsize=12)
ax.legend()
ax.set_xlim(-2, 8)
ax.set_ylim(0, None)
plt.tight_layout()
plt.show()
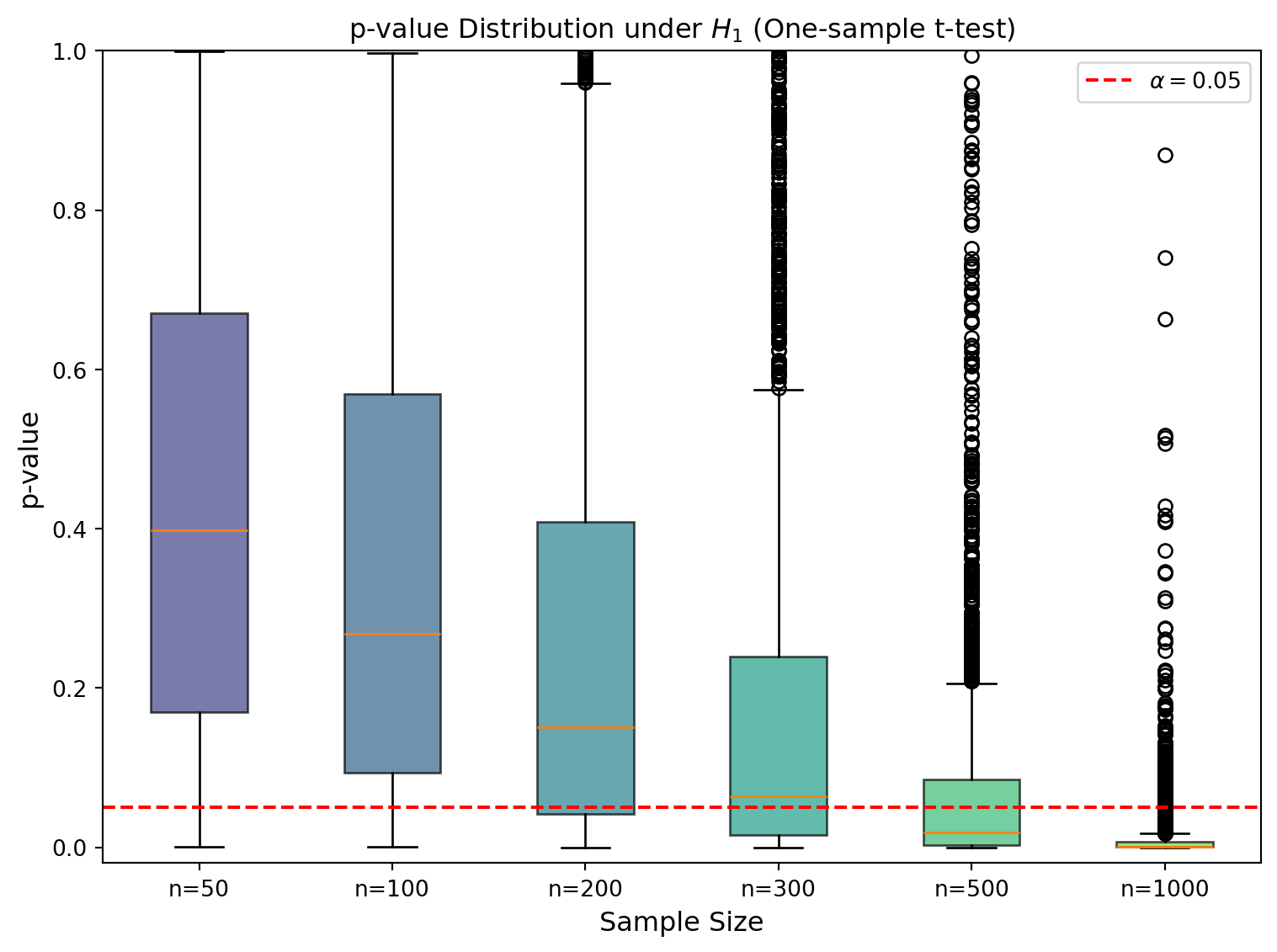
\(H_1\) が真である状況で,サンプルサイズ \(n\) を変えたときの p-value の分布を確認します.
まず,理論検出力を計算します.\(H_0: \mu = 0\) に対する片側 t 検定の検出力は,非心度パラメータ
\[
\delta = \frac{\mu - \mu_0}{\sigma / \sqrt{n}} = \frac{0.15}{\sqrt{2} / \sqrt{n}} = 0.15 \sqrt{n/2}
\]
を用いて,非心 t 分布から計算できます(\(\text{Gamma}(2,1)\) の分散は 2).
理論検出力
import polars as pl
# パラメータ
alpha = 0.05
mu_true = 0.15
sigma = np.sqrt(2) # Gamma(2,1) の標準偏差
sample_sizes = [50, 100, 200, 300, 500, 1000]
# 理論検出力の計算
power_results = []
for n in sample_sizes:
# 非心度パラメータ
ncp = mu_true / (sigma / np.sqrt(n))
# 臨界値 (中心t分布)
t_crit = stats.t.ppf(1 - alpha / 2, df=n-1)
# 検出力 (非心t分布)
power = 1 - stats.nct.cdf(t_crit, df=n-1, nc=ncp)
power_results.append({"n": n, "非心度 $\delta$": round(ncp, 3), "理論検出力": round(power, 3)})
pl.DataFrame(power_results)
shape: (6, 3)
| i64 |
f64 |
f64 |
| 50 |
0.75 |
0.11 |
| 100 |
1.061 |
0.182 |
| 200 |
1.5 |
0.32 |
| 300 |
1.837 |
0.449 |
| 500 |
2.372 |
0.658 |
| 1000 |
3.354 |
0.918 |
p-value シミュレーション
np.random.seed(42)
# パラメータ
sample_sizes = [50, 100, 200, 300, 500, 1000]
n_simulations = 2000
# シミュレーション
results = {n: [] for n in sample_sizes}
for n in sample_sizes:
for _ in range(n_simulations):
# ガンマ分布からサンプル生成 (E[X] = 2 - 1.85 = 0.15, 右に歪んだ分布)
X = np.random.gamma(shape=2, scale=1, size=n) - 1.85
# one-sample t検定 (H1: mean != 0)
t_stat, p_two_sided = stats.ttest_1samp(X, popmean=0, alternative="two-sided")
# 片側検定に変換
results[n].append(p_two_sided)
# Box plot
fig, ax = plt.subplots(figsize=(8, 6))
data = [results[n] for n in sample_sizes]
bp = ax.boxplot(data, tick_labels=[f"n={n}" for n in sample_sizes], patch_artist=True)
# 色設定
colors = plt.cm.viridis(np.linspace(0.2, 0.8, len(sample_sizes)))
for patch, color in zip(bp["boxes"], colors):
patch.set_facecolor(color)
patch.set_alpha(0.7)
ax.axhline(y=0.05, color="red", linestyle="--", label=r"$\alpha = 0.05$")
ax.set_xlabel("Sample Size", fontsize=12)
ax.set_ylabel("p-value", fontsize=12)
ax.set_title(r"p-value Distribution under $H_1$ (One-sample t-test)", fontsize=12)
ax.legend()
ax.set_ylim(-0.02, 1.0)
plt.tight_layout()
plt.show()
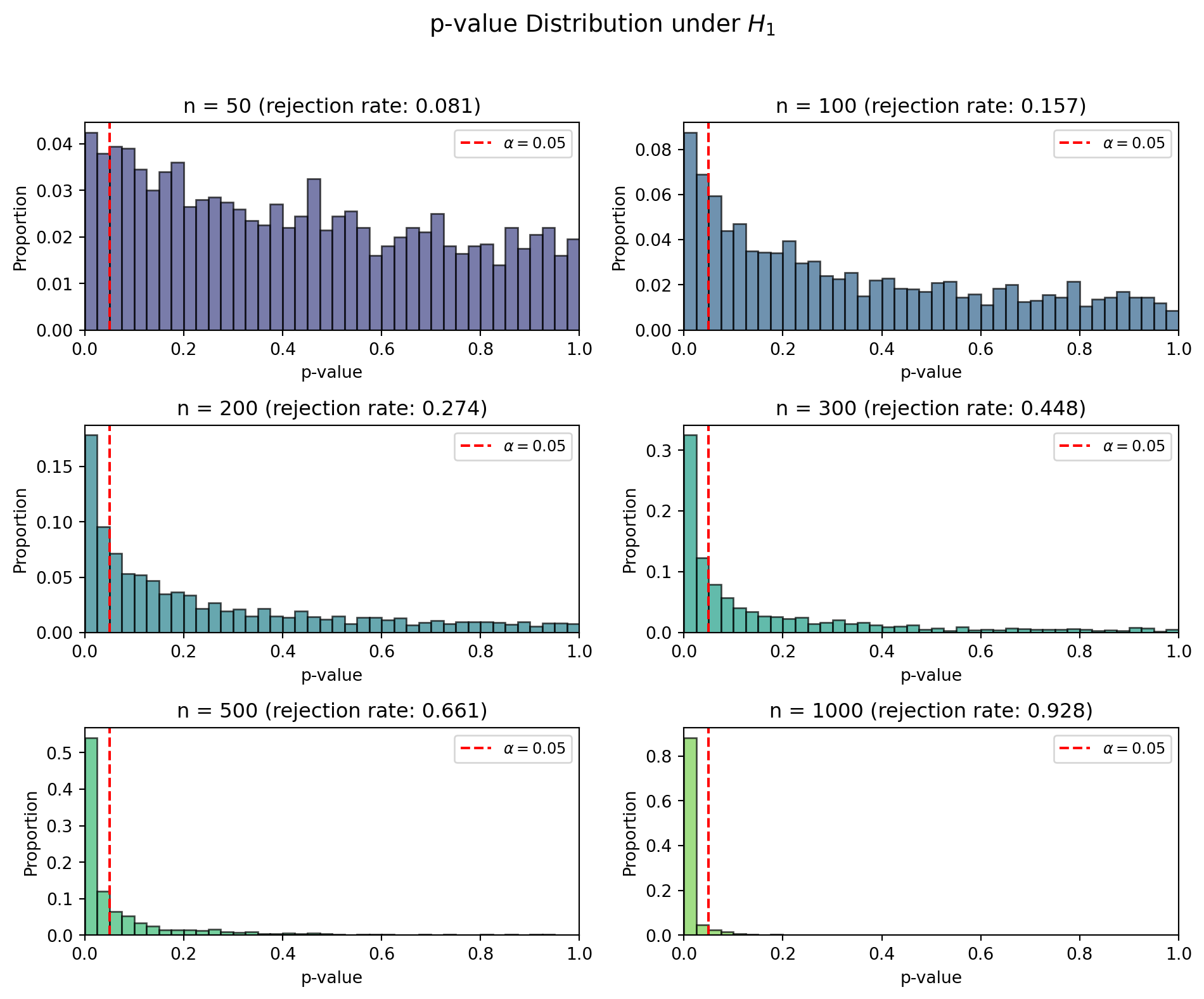
p-value 分布のヒストグラム
fig, axes = plt.subplots(3, 2, figsize=(10, 8))
axes = axes.flatten()
for idx, n in enumerate(sample_sizes):
ax = axes[idx]
bins = np.arange(0, 1.025, 0.025) # 0.05刻み
ax.hist(
results[n],
bins=bins,
weights=np.ones(len(results[n])) / len(results[n]),
alpha=0.7,
color=colors[idx],
edgecolor="black",
)
ax.axvline(x=0.05, color="red", linestyle="--", lw=1.5, label=r"$\alpha = 0.05$")
# シミュレーションでの棄却率
rejection_rate = np.mean(np.array(results[n]) < 0.05)
ax.set_title(f"n = {n} (rejection rate: {rejection_rate:.3f})", fontsize=12)
ax.set_xlabel("p-value", fontsize=10)
ax.set_ylabel("Proportion", fontsize=10)
ax.set_xlim(0, 1)
ax.legend(fontsize=9)
plt.suptitle(r"p-value Distribution under $H_1$", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()
\(H_1\) が真である状況では,サンプルサイズが大きくなるほど検出力が上がり,p-value は小さい値に集中していきます.シミュレーションによる棄却率は理論検出力とほぼ一致することが確認できます.
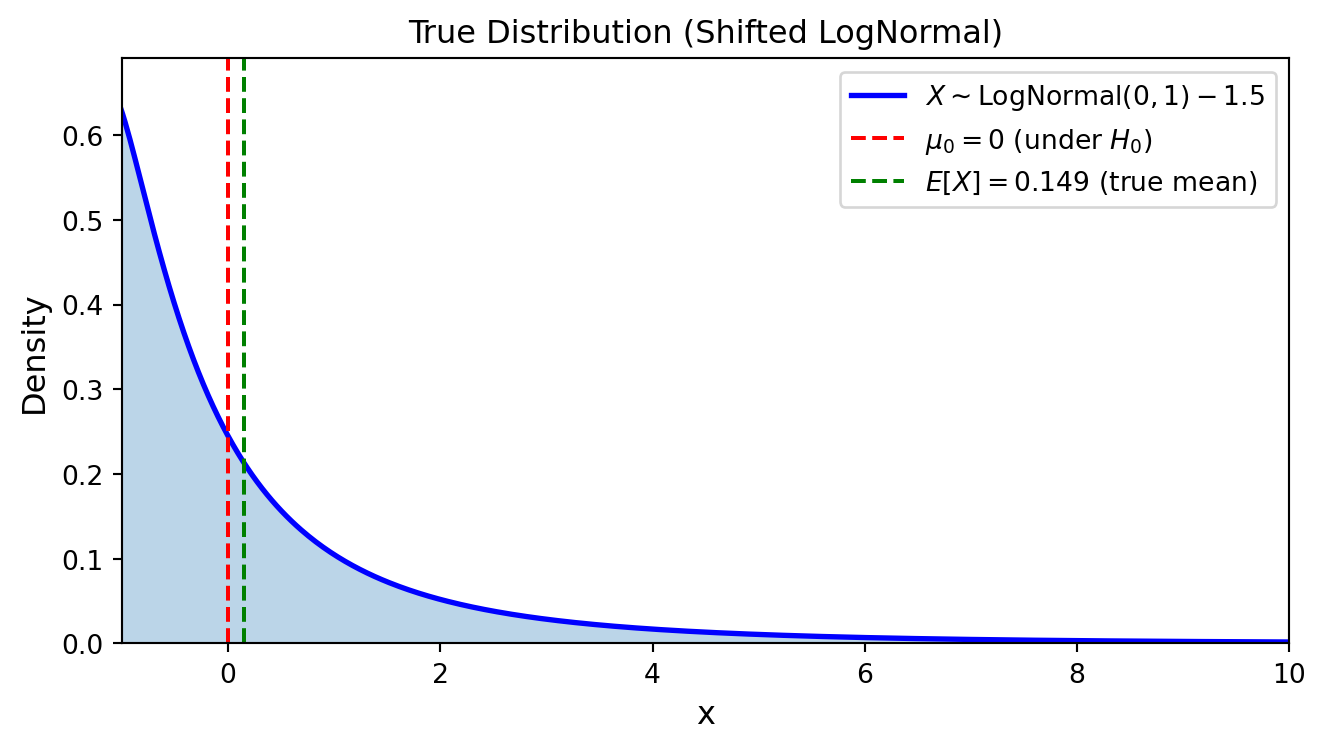
対数正規分布の場合
より裾が重い分布として,\(X \sim \text{LogNormal}(0, 1) - 1.5\) を考えます(\(E[X] = e^{0.5} - 1.5 \approx 0.149 > 0\)). この確率変数列に対して, one-sample t 検定を行います.
対数正規分布の真の分布
# 対数正規分布 - 1.5 の確率密度関数
shift_ln = 1.5
x_ln = np.linspace(-1.5, 10, 500)
pdf_ln = stats.lognorm.pdf(x_ln + shift_ln, s=1, scale=np.exp(0))
mu_ln = np.exp(0.5) - shift_ln # E[X] = exp(mu + sigma^2/2) - shift
sigma_ln = np.sqrt(
(np.exp(1) - 1) * np.exp(1)
) # Var[X] = (exp(sigma^2) - 1) * exp(2mu + sigma^2)
fig, ax = plt.subplots(figsize=(7, 4))
ax.plot(x_ln, pdf_ln, "b-", lw=2, label=r"$X \sim \mathrm{LogNormal}(0, 1) - 1.5$")
ax.fill_between(x_ln, pdf_ln, alpha=0.3)
ax.axvline(x=0, color="red", linestyle="--", lw=1.5, label=r"$\mu_0 = 0$ (under $H_0$)")
ax.axvline(
x=mu_ln,
color="green",
linestyle="--",
lw=1.5,
label=f"$E[X] = {mu_ln:.3f}$ (true mean)",
)
ax.set_xlabel("x", fontsize=12)
ax.set_ylabel("Density", fontsize=12)
ax.set_title("True Distribution (Shifted LogNormal)", fontsize=12)
ax.legend()
ax.set_xlim(-1, 10)
ax.set_ylim(0, None)
plt.tight_layout()
plt.show()
理論検出力(対数正規分布)
# 理論検出力の計算
power_results_ln = []
for n in sample_sizes:
ncp = mu_ln / (sigma_ln / np.sqrt(n))
t_crit = stats.t.ppf(1 - alpha / 2, df=n - 1)
power = 1 - stats.nct.cdf(t_crit, df=n - 1, nc=ncp)
power_results_ln.append(
{"n": n, "非心度 $\delta$": round(ncp, 3), "理論検出力": round(power, 3)}
)
pl.DataFrame(power_results_ln)
shape: (6, 3)
| i64 |
f64 |
f64 |
| 50 |
0.487 |
0.069 |
| 100 |
0.688 |
0.101 |
| 200 |
0.973 |
0.161 |
| 300 |
1.192 |
0.22 |
| 500 |
1.539 |
0.336 |
| 1000 |
2.176 |
0.585 |
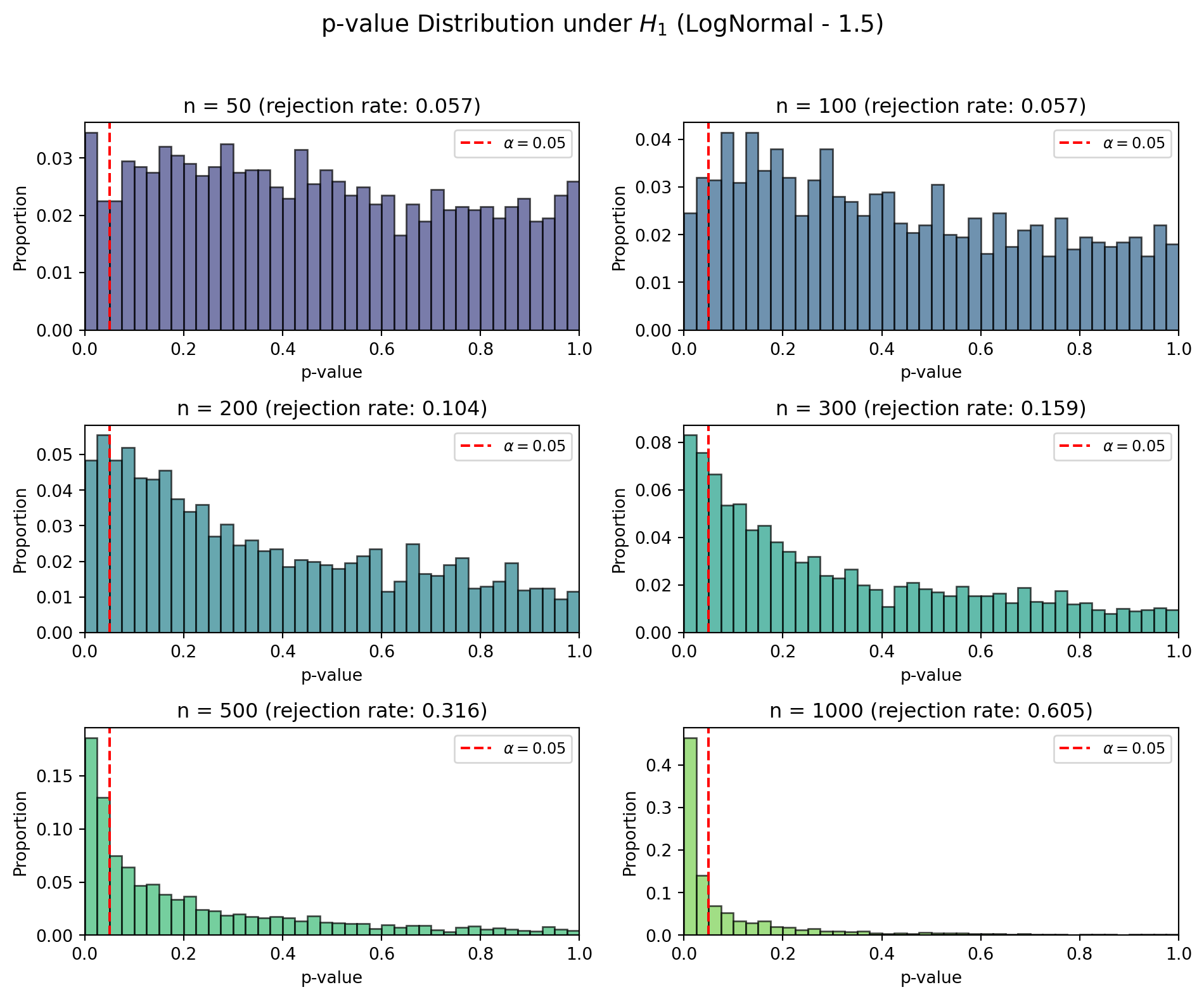
p-value シミュレーション(対数正規分布)
np.random.seed(42)
# シミュレーション
results_ln = {n: [] for n in sample_sizes}
means_ln = {n: [] for n in sample_sizes}
for n in sample_sizes:
for _ in range(n_simulations):
X = np.random.lognormal(mean=0, sigma=1, size=n) - 1.5
means_ln[n].append(np.mean(X))
t_stat, p_one_sided = stats.ttest_1samp(X, popmean=0, alternative="two-sided")
results_ln[n].append(p_one_sided)
# ヒストグラム
fig, axes = plt.subplots(3, 2, figsize=(10, 8))
axes = axes.flatten()
for idx, n in enumerate(sample_sizes):
ax = axes[idx]
bins = np.arange(0, 1.025, 0.025)
ax.hist(
results_ln[n],
bins=bins,
weights=np.ones(len(results_ln[n])) / len(results_ln[n]),
alpha=0.7,
color=colors[idx],
edgecolor="black",
)
ax.axvline(x=0.05, color="red", linestyle="--", lw=1.5, label=r"$\alpha = 0.05$")
rejection_rate = np.mean(np.array(results_ln[n]) < 0.05)
ax.set_title(f"n = {n} (rejection rate: {rejection_rate:.3f})", fontsize=12)
ax.set_xlabel("p-value", fontsize=10)
ax.set_ylabel("Proportion", fontsize=10)
ax.set_xlim(0, 1)
ax.legend(fontsize=9)
plt.suptitle(r"p-value Distribution under $H_1$ (LogNormal - 1.5)", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()
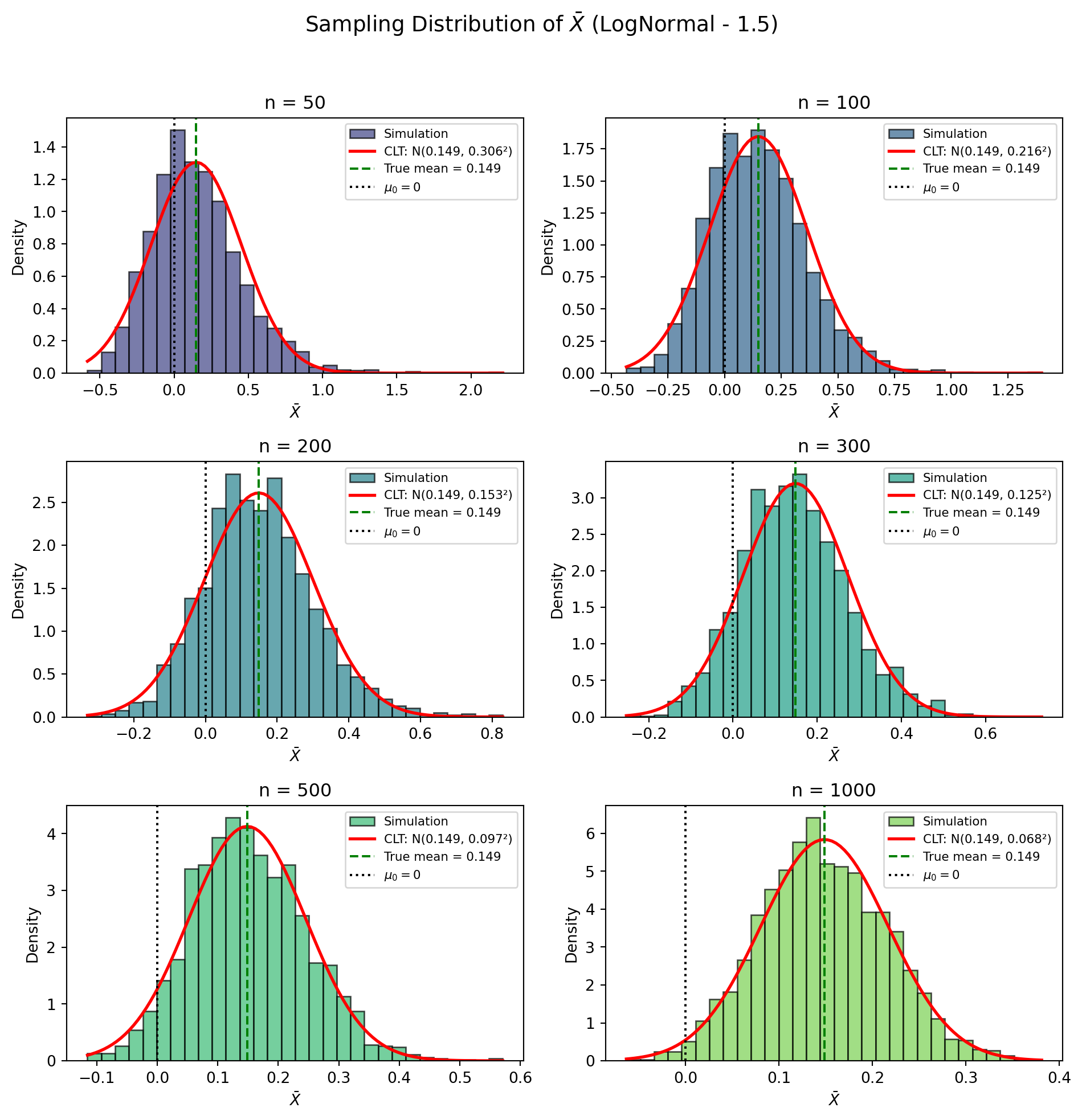
標本平均の分布(対数正規分布)
fig, axes = plt.subplots(3, 2, figsize=(10, 10))
axes = axes.flatten()
for idx, n in enumerate(sample_sizes):
ax = axes[idx]
mean_data = np.array(means_ln[n])
# ヒストグラム
ax.hist(
mean_data,
bins=30,
density=True,
alpha=0.7,
color=colors[idx],
edgecolor="black",
label="Simulation",
)
# 理論的な正規分布(CLT)
se = sigma_ln / np.sqrt(n)
x_norm = np.linspace(mean_data.min(), mean_data.max(), 100)
ax.plot(
x_norm,
stats.norm.pdf(x_norm, loc=mu_ln, scale=se),
"r-",
lw=2,
label=f"CLT: N({mu_ln:.3f}, {se:.3f}²)",
)
ax.axvline(
x=mu_ln, color="green", linestyle="--", lw=1.5, label=f"True mean = {mu_ln:.3f}"
)
ax.axvline(x=0, color="black", linestyle=":", lw=1.5, label=r"$\mu_0 = 0$")
ax.set_title(f"n = {n}", fontsize=12)
ax.set_xlabel(r"$\bar{X}$", fontsize=10)
ax.set_ylabel("Density", fontsize=10)
ax.legend(fontsize=8)
plt.suptitle(
r"Sampling Distribution of $\bar{X}$ (LogNormal - 1.5)", fontsize=14, y=1.02
)
plt.tight_layout()
plt.show()
対数正規分布はガンマ分布より裾が重く歪みも大きいため,t検定の正規性仮定からの乖離が大きくなります.標本平均の分布を見ると,サンプルサイズが小さいときは右に歪んでいますが,\(n\) が大きくなるとCLTにより正規分布に近づいていくことが確認できます.
Appendix: \(H_1: \mu > 0\) のときのp-valueの分布
\(\{X_i\}_{i=1}^n \overset{\mathrm{iid}}{\sim} G(\mu, \sigma^2)\) となる確率変数列に対するone-sample t testを考えます.
\[
\left\{\begin{array}{c}
H_0: \mu \leq 0\\
H_1: \mu > 0
\end{array}\right.
\]
と帰無仮説と対立仮説を設定し,検定統計量 \(T\) は
\[
T = \frac{\bar X - \mu_0}{\hat\sigma / \sqrt{n}}
\]
とします.データから \(T = t_0\) を得られたとして,このときのp-valueは定義より
\[
\text{p-value} = \operatorname{Pr}(T > t_0 | H_0) = 1 - F_{t(n-1)}(t_0)
\]
CLTが成立するとすると
\[
\bar{X} \sim N\left(\mu, \frac{\sigma^2}{n}\right)
\]
したがって,\(H_1\) が真のときの \(T\) は漸近的に
\[
T = \frac{\bar{X} - \mu_1}{\sigma/\sqrt{n}}\frac{\sigma}{\hat\sigma} + \frac{\mu_1 - \mu_0}{\sigma/\sqrt{n}}\frac{\sigma}{\hat\sigma}
\]
RHSの第一項は連続写像定理およびSlutskyの定理より \(N(0, 1)\) に分布収束.RHSの第二項が非心パラメータ \(\delta\) として
\[
\delta = \frac{\mu_1}{\sigma/\sqrt{n}}
\]
したがって,
\[
T \sim N\left(\frac{\mu_1}{\sigma/\sqrt{n}}, 1\right)
\]
このとき,p-valueの分布関数 \(F_p\) は
\[
\begin{align}
F_p(\alpha)
&= \operatorname{Pr}(\text{p-value}\leq \alpha)\\[5pt]
&= \operatorname{Pr}(1 - F_{t(n-1)}(T) \leq \alpha)\\[5pt]
&= 1 - \operatorname{Pr}(F_{t(n-1)}(T) \leq 1- \alpha)\\[5pt]
&= 1 - \operatorname{Pr}(T \leq F_{t(n-1)}^{-1}(1- \alpha))\\[5pt]
&= 1 - \Phi\left(F_{t(n-1)}^{-1}(1- \alpha) - \frac{\mu_1}{\sigma/\sqrt{n}}\right)
\end{align}
\]
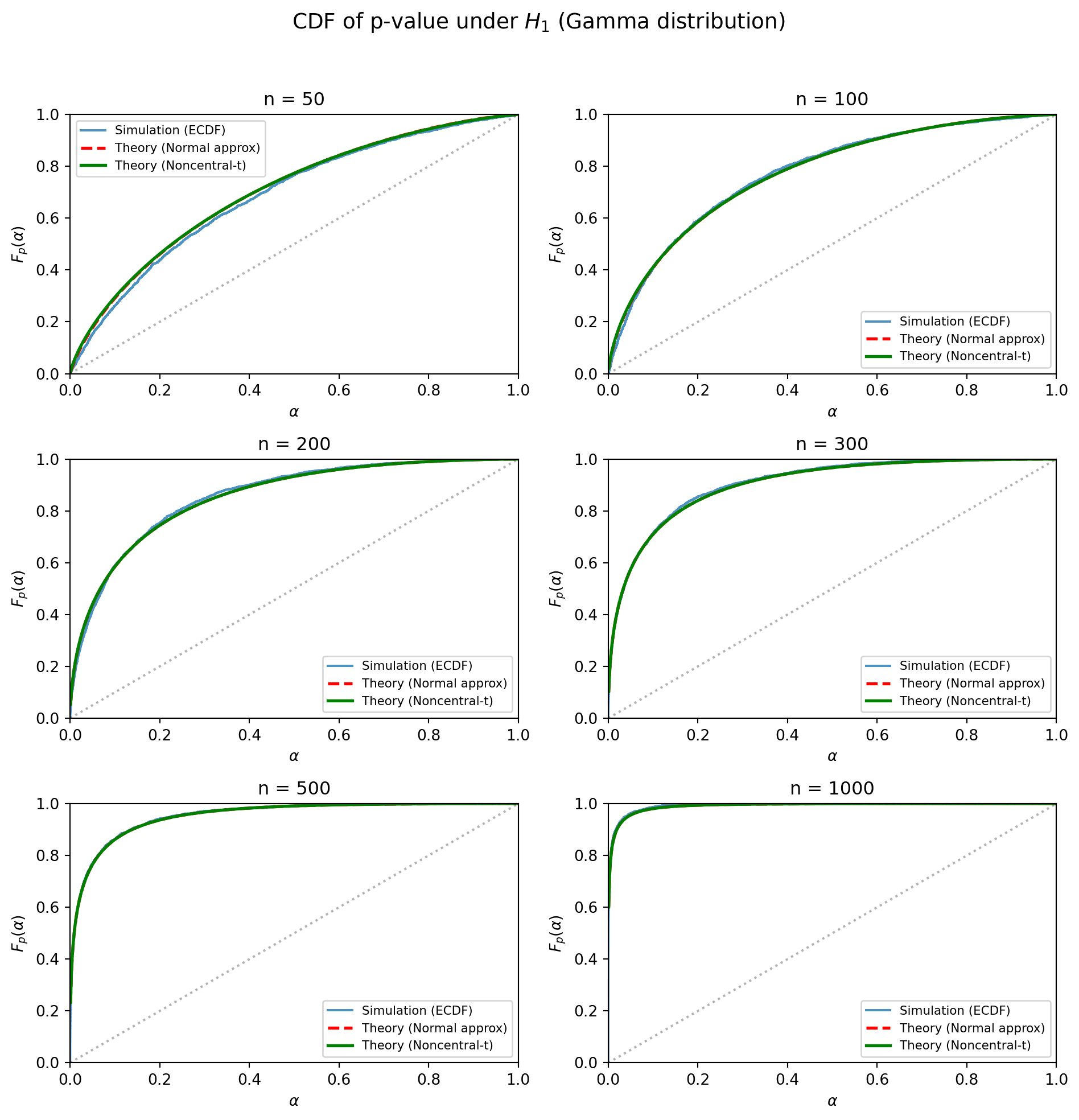
Example 2 (ガンマ分布one-sample test p-value CDFのシミュレーション)
Code
# パラメータ(Gamma分布の場合)
mu_1 = 0.15 # 真の平均
sigma = np.sqrt(2) # Gamma(2,1) の標準偏差
def theoretical_pvalue_cdf(alpha, n, mu_1, sigma):
"""
理論的なp-value分布のCDF(漸近近似)
F_p(alpha) = 1 - Φ(F_{t(n-1)}^{-1}(1-alpha) - μ_1/(σ/√n))
"""
delta = mu_1 / (sigma / np.sqrt(n)) # 非心度
t_quantile = stats.t.ppf(1 - alpha, df=n - 1)
return 1 - stats.norm.cdf(t_quantile - delta)
# プロット
fig, axes = plt.subplots(3, 2, figsize=(10, 10))
axes = axes.flatten()
alpha_grid = np.linspace(0.001, 1, 500)
# シミュレーション
results_one_sieded = {n: [] for n in sample_sizes}
for n in sample_sizes:
for _ in range(n_simulations):
# ガンマ分布からサンプル生成 (E[X] = 2 - 1.85 = 0.15, 右に歪んだ分布)
X = np.random.gamma(shape=2, scale=1, size=n) - 1.85
# one-sample t検定 (H1: mean != 0)
t_stat, p_one_sided = stats.ttest_1samp(X, popmean=0, alternative="greater")
# 片側検定に変換
results_one_sieded[n].append(p_one_sided)
for idx, n in enumerate(sample_sizes):
ax = axes[idx]
# シミュレーションによる経験的CDF
sorted_pvals = np.sort(results_one_sieded[n])
empirical_cdf = np.arange(1, len(sorted_pvals) + 1) / len(sorted_pvals)
ax.step(
sorted_pvals, empirical_cdf, where="post", label="Simulation (ECDF)", alpha=0.8
)
# 理論的CDF(漸近正規近似)
theoretical_cdf = [theoretical_pvalue_cdf(a, n, mu_1, sigma) for a in alpha_grid]
ax.plot(alpha_grid, theoretical_cdf, "r--", lw=2, label="Theory (Normal approx)")
# 非心t分布による理論CDF(より正確)
delta = mu_1 / (sigma / np.sqrt(n))
t_quantiles = stats.t.ppf(1 - alpha_grid, df=n - 1)
theoretical_cdf_nct = 1 - stats.nct.cdf(t_quantiles, df=n - 1, nc=delta)
ax.plot(alpha_grid, theoretical_cdf_nct, "g-", lw=2, label="Theory (Noncentral-t)")
ax.set_xlabel(r"$\alpha$", fontsize=10)
ax.set_ylabel(r"$F_p(\alpha)$", fontsize=10)
ax.set_title(f"n = {n}", fontsize=12)
ax.legend(fontsize=8)
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.plot([0, 1], [0, 1], "k:", alpha=0.3, label="Uniform (under $H_0$)")
plt.suptitle(r"CDF of p-value under $H_1$ (Gamma distribution)", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()
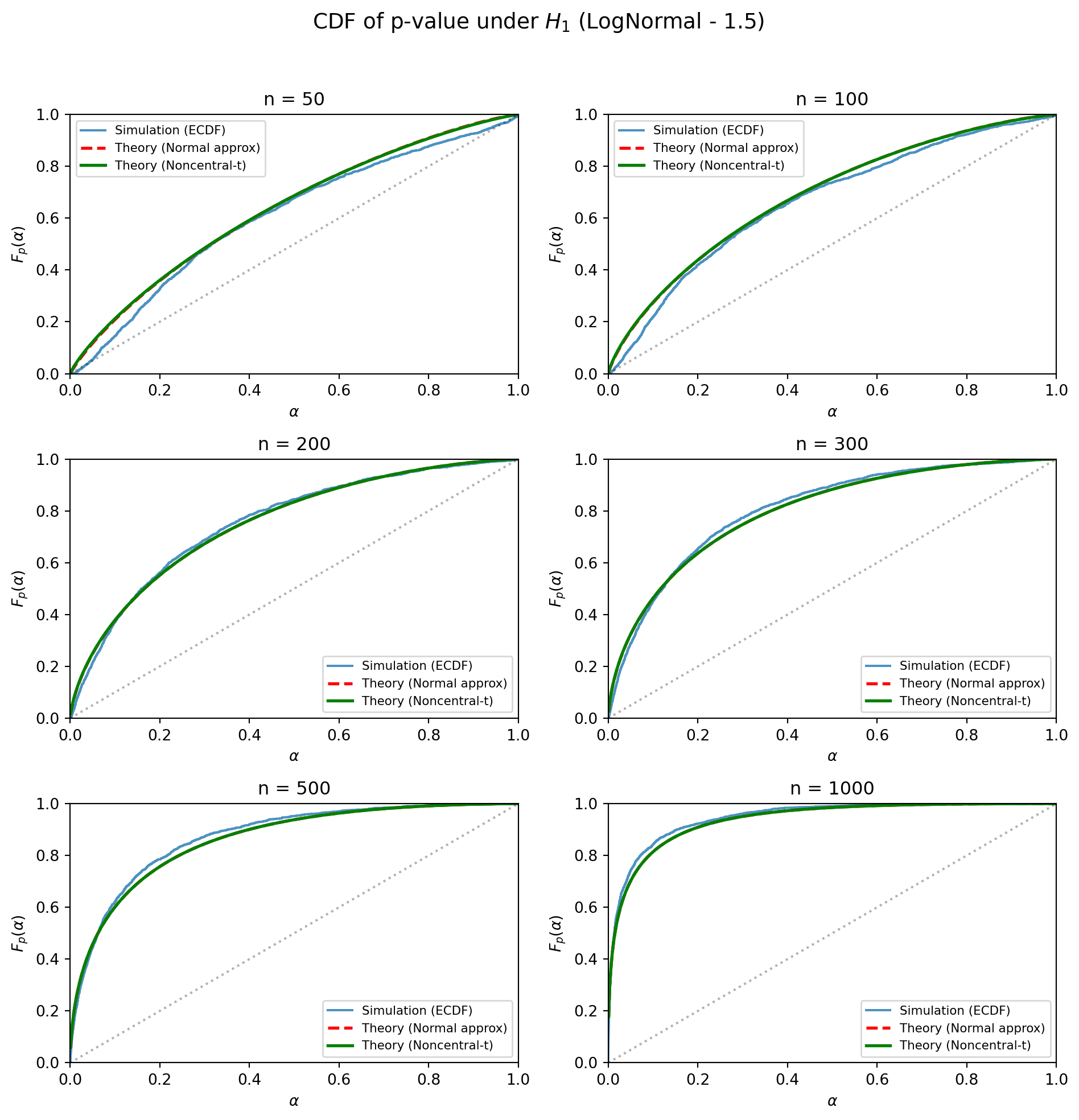
Example 3 (対数正規分布 one-sample test p-value CDFのシミュレーション)
Code
# パラメータ(対数正規分布の場合)
# mu_ln, sigma_ln は既に定義済み
# プロット
fig, axes = plt.subplots(3, 2, figsize=(10, 10))
axes = axes.flatten()
alpha_grid = np.linspace(0.001, 1, 500)
# シミュレーション
results_ln_one_sided = {n: [] for n in sample_sizes}
means_ln = {n: [] for n in sample_sizes}
for n in sample_sizes:
for _ in range(n_simulations):
X = np.random.lognormal(mean=0, sigma=1, size=n) - 1.5
means_ln[n].append(np.mean(X))
t_stat, p_one_sided = stats.ttest_1samp(X, popmean=0, alternative="greater")
results_ln_one_sided[n].append(p_one_sided)
for idx, n in enumerate(sample_sizes):
ax = axes[idx]
# シミュレーションによる経験的CDF
sorted_pvals = np.sort(results_ln_one_sided[n])
empirical_cdf = np.arange(1, len(sorted_pvals) + 1) / len(sorted_pvals)
ax.step(
sorted_pvals, empirical_cdf, where="post", label="Simulation (ECDF)", alpha=0.8
)
# 理論的CDF(漸近正規近似)
theoretical_cdf = [
theoretical_pvalue_cdf(a, n, mu_ln, sigma_ln) for a in alpha_grid
]
ax.plot(alpha_grid, theoretical_cdf, "r--", lw=2, label="Theory (Normal approx)")
# 非心t分布による理論CDF(より正確)
delta = mu_ln / (sigma_ln / np.sqrt(n))
t_quantiles = stats.t.ppf(1 - alpha_grid, df=n - 1)
theoretical_cdf_nct = 1 - stats.nct.cdf(t_quantiles, df=n - 1, nc=delta)
ax.plot(alpha_grid, theoretical_cdf_nct, "g-", lw=2, label="Theory (Noncentral-t)")
ax.set_xlabel(r"$\alpha$", fontsize=10)
ax.set_ylabel(r"$F_p(\alpha)$", fontsize=10)
ax.set_title(f"n = {n}", fontsize=12)
ax.legend(fontsize=8)
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.plot([0, 1], [0, 1], "k:", alpha=0.3, label="Uniform (under $H_0$)")
plt.suptitle(r"CDF of p-value under $H_1$ (LogNormal - 1.5)", fontsize=14, y=1.02)
plt.tight_layout()
plt.show()