感染症有病率推定量と意思決定
Exercise 1.1
人口 \(1000\) 人からなる地域Aの公衆衛生政策担当者を想定します.とある感染症が世界的に流行しており,公衆衛生担当者として全市民にワクチン接種を強制するか否かの意思決定に直面しています.
▶ 政策意思決定に関連する情報
政策意思決定に関連する情報として以下のことがわかっています
- ワクチンの費用は摂取人数あたり100円(=つまり,ワクチンを矯正すると一人あたり施策実施費用は100円,otherwise 0円)
- 健康な人の一人あたりのGDPは1000円だが,感染症に罹患すると500円まで下がる
- 感染症に罹患した人にワクチンを投与すると,一人あたりのGDPは500円→1000円まで回復する
▶ 仮定
地域の住民 \(i\) が感染症に罹患しているか否かを表す確率変数 \(Y_i\) は
\[
Y_i \overset{\mathrm{iid}}{\sim} \operatorname{Bernoulli}(\theta)
\]
そして,街全体の感染者人数を
\[
Y = \sum_{i=1}^{1000} Y_i
\]
と表すとします.\(\theta\) は公衆衛生政策担当者にとっては未知であるが,事前の情報として,少し古い情報だが地域Aと似たような地域では 平均 \(0.1\), 区間 \(0.01\) から \(0.25\) の間で分布していることがわかっているとします.
▶ 直面している意思決定問題
Decision変数 \(d\) を以下のように表すとする
\[
\begin{align*}
d = \left\{\begin{array}{c}
1 & \text{ワクチン接種強制}\\
0 & \text{otherwise}
\end{array}\right.
\end{align*}
\]
地域Aの \(U = \text{GDP}(Y, d) - \text{施策費用}\times d\) の期待値を最大化する観点から公衆衛生政策担当者は \(d\) をどのように決定すればよいか?
データに基づいて公衆衛生政策担当者の行う判断を決定(decision)とするとき,その決定は \(d\) という変数で上記のように表されています.このとき,決定 \(d\) の集合について一般に決定空間とと呼び,多くの場合 \(D\) で表されます.
問題設定より,決定空間 \(D\) は
\[
D = \{\text{住民へのワクチン接種強制実施}, \text{住民へのワクチン接種強制不実施}\}
\]
となります.
▶ パラメータ空間
意思決定にあたって関心があるのは,街で感染した人の割合 \(\theta\) です.大まかに言えば,\(\theta\) のパラメーター空間 \(\Theta\) は0と1の間のすべての値になるので
\[
\Theta = [0, 1]
\]
▶ 損失関数
地域Aの \(U = \text{GDP} - \text{施策費用}\) の期待値の最大化問題は,
\[
\begin{align*}
\mathop{\mathrm{argmax}}_d\, \mathbb E[U]
&= \mathbb E[\sum_{i=1}^{1000} (\text{GDP}(Y, d)_i - 100d)]\\
&= \sum_{i=1}^{1000}\mathbb E[\text{GDP}(Y_i, d)_i - 100d]\\
&= 1000 \times \mathbb E[\text{GDP}(Y_i, d)_i - 100d]
\end{align*}
\]
したがって,
\[
\mathop{\mathrm{argmax}}_d\, \mathbb E[\text{GDP}_i(Y_i, d) - 100d]
\tag{1.1}\]
の問題を解けば良いことがわかります.最大化問題の形式でも良いですが,これを損失関数の形で表現し直します.このとき, \(c_{ij}\) を成分とする損失行列 \(C\) は
|
|
|
\(Y_i=1\)
|
\(Y_i=0\)
|
|
\(d=1\)
|
\(100\)
|
\(100\)
|
|
\(d=0\)
|
\(500\)
|
\(0\)
|
- \(Y_i=0, Y_i=1\) のどちらでも \(d=1\) のときは一人あたりGDPは \(1000\), but 施策費用 \(100\) が発生 → 損失は \(100\)
- \(Y_i=1\) のとき \(d=0\) は 一人あたりGDPが \(1000 \to 500\) へ下がる → 損失は \(500\)
このコスト行列をベースにワクチン接種強制についての決定変数 \(d\) に応じた損失関数 \(L(d)\) を用いて@eq-objective-func を表現し直すと
\[
\mathop{\mathrm{argmin}}_d\, \mathbb E[L(d)] = \sum_{j\in\{0, 1\}} C(d, Y_i=j)p(Y_i =j)
\]
\(d\) に応じた損失関数 \(L(d)\) の期待値を計算すると
\[
\begin{align*}
\mathbb E[L(d=1)] &= 100\\
\mathbb E[L(d=0)] &= 500 \times \mathbb E[Y_i = 1] = 500 \times p(Y_i = 1)
\end{align*}
\]
ここから損失最小化問題の解として
\[
d = \left\{\begin{array}{c}
1 & \text{if } p(Y_i = 1) > 0.2\\
\{0, 1\} & \text{if } p(Y_i = 1) = 0.2\\
0 & \text{if } p(Y_i = 1) < 0.2
\end{array}\right.
\]
となることがわかります.
▶ \(p(Y_i=1)\)と信念
問題文より
\[
Y_i \overset{\mathrm{iid}}{\sim} \operatorname{Bernoulli}(\theta)
\]
したがって,\(p(Y_i=1) = \theta\) となりますが,\(\theta\) は政策担当者にとって未知の変数です.
一方,\(\theta\) について「少し古い情報だが地域Aと似たような地域では 平均 \(0.1\), 区間 \(0.01\) から \(0.25\) の間で分布している」という情報があります. この政策担当者の \(\theta\) に対する事前の信念が\(p(\theta)\) という形で表現されるとします.このとき,
\[
\begin{align*}
p(Y_i=1)
&= \int_\Theta p(Y_i = 1, \theta) \,\mathrm{d} \theta\\
&= \int_\Theta p(Y_i = 1\vert \theta) p(\theta) \,\mathrm{d} \theta\\
&= \int_\Theta \theta p(\theta) \,\mathrm{d} \theta\\
&= \mathbb E[\theta]
\end{align*}
\]
「少し古い情報だが地域Aと似たような地域では 平均 \(0.1\), 区間 \(0.01\) から \(0.25\) の間で分布している」を表す政策担当者の信念を表す分布 \(p(\theta)\) は無数に存在し得りますが, 「あやゆるモデルは誤りであるが,いくつかは有用である」(Box and Draper, 11987)という格言に従って,信念を近似する関数を
\[
\theta \sim \operatorname{Beta}(2, 18)
\tag{1.2}\]
などで近似し,観察データに基づいて信念を更新,更新された信念に基いて意思決定をしていきます.
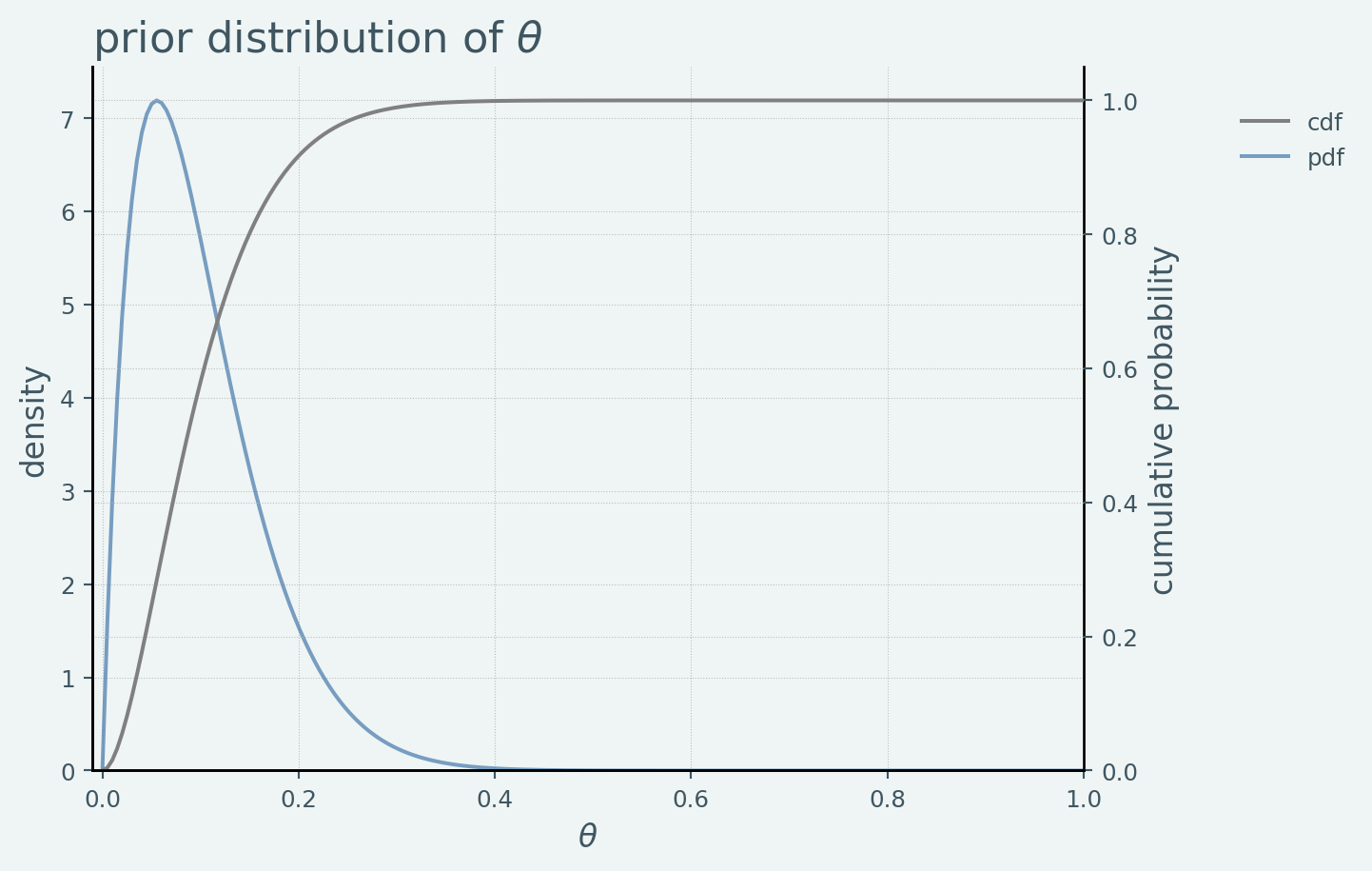
▶ ベータ分布による信念の近似
Equation 1.2 を政策担当者の信念の近似分布とすると以下のようなPDF, CDFになります.
Code
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt
import regmonkey_style.stylewizard as sw
sw.set_templates("regmonkey_scatter")
a = 2
b= 18
x = np.linspace(0, 1, 200)
rv = beta(a, b)
fig, ax1 = plt.subplots(1, 1)
ax2 = ax1.twinx()
ax1.plot(x, rv.pdf(x))
ax2.plot(x, rv.cdf(x), color='gray')
ax1.set_xlabel(r'$\theta$')
ax1.set_ylabel(r'density')
ax2.set_ylabel(r'cumulative probability')
ax1.set_ylim(0,)
ax1.set_xlim(-0.01,1)
ax2.set_xlim(-0.01,1)
ax2.set_ylim(0,)
ax1.spines[['right']].set_visible(True)
ax1.set_title(r"prior distribution of $\theta$")
ax1.legend(labels=['pdf'],loc=2, borderaxespad=0., bbox_to_anchor=(1.15, 0.9))
ax2.legend(labels=['cdf'],loc=2, borderaxespad=0., bbox_to_anchor=(1.15, 0.95))
plt.show()
\(X\sim \operatorname{Beta}(a, b)\) とすると,
\[
\begin{align*}
\operatorname{mode}(X) &= \frac{a-1}{a + b - 2}\\
\mathbb E[X] &= \frac{a}{a+b}
\end{align*}
\]
であるので,\(\mathbb E[\theta] = \frac{2}{2+18} = 0.1\) となるので 「少し古い情報だが地域Aと似たような地域では 平均 \(0.1\), 区間 \(0.01\) から \(0.25\) の間で分布している」という情報をある程度近似していると判断することができます.また,区間 \(0.01\) から \(0.25\) の確率は
Code
from IPython.display import display, Markdown
prob = rv.cdf(0.25) - rv.cdf(0.01)
display(Markdown(rf"$Pr(0.01 \leq \theta \leq 0.25) = {prob:.4f}$"))
\(Pr(0.01 \leq \theta \leq 0.25) = 0.9537\)
事前分布の更新
ワクチン接種強制の意思決定をするにあたって,地域Aの住民から無作為に43人選び感染の検査を行うことにした. 感染者人数がデータ \(x\) で表されるとき,その標本空間 \(\mathcal{X}\) は
\[
\mathcal{X} = \{0, 1, \cdots, 43\}
\]
また標本モデルは
\[
X \vert \theta \sim \operatorname{binomial}(43, \theta)
\]
▶ ベイズルールに基づく事後分布の更新
ベイズルールより \(X\) を観測した後の \(\theta\) に関する事後分布は,\(p(\theta)\) を事前分布とすると
\[
p(\theta\vert X) = \frac{p(X\vert \theta)p(\theta)}{p(X)}
\]
また,
\[
\begin{align*}
p(X) &= \int^1_0 {_{n}}C_x \theta^x(1-\theta)^{n-x} p(\theta) \,\mathrm{d}\theta \\[8pt]
&= \int^1_0 \frac{_{n}C_x}{B(a, b)} \theta^x(1-\theta)^{n-x}\theta^{a - 1}(1-\theta)^{b - 1}\,\mathrm{d}\theta\\[8pt]
&=\int^1_0 \frac{_{n}C_x}{B(a, b)} \theta^{a+x-1}(1-\theta)^{b + n-x - 1}\,\mathrm{d}\theta\\
&= \frac{_{n}C_x}{B(a, b)}B(a + x, b + n - x)
\end{align*}
\]
したがって,事後分布 \(p(\theta\vert X)\) は
\[
\begin{align*}
p(\theta\vert X)
= \frac{1}{B(a+x, b+n-x-1)}\theta^{a+x-1}(1-\theta)^{b+n-x-1}
\end{align*}
\]
よって,事後分布は以下のように更新されます
\[
\theta\vert X \sim \operatorname{Beta}(a+x, b+n-x)
\tag{1.3}\]
▶ cmdstanpyによる推定
政策担当者が\(N=43\) の調査をした結果,サンプルにおける感染者人数 \(X\) は \(11\) であることがわかったとします.
Equation 1.2, Equation 1.3 より
\[
\begin{align*}
\mathbb E[\theta \vert X] &= \frac{13}{63} \approx 0.20635\\
\operatorname{mode}(\theta \vert X) &= \frac{12}{61} \approx 0.1967
\end{align*}
\]
となるはずです.これをcmdstanpyで計算します.stan modelを以下のように記述します.
data {
int<lower=0> N; // number of observations
// array[N] int<lower=0, upper=1> Y; // outcomes
int<lower=0> X;
real<lower=0> alpha; // prior hyperparameter
real<lower=0> beta; // prior hyperparameter
}
parameters {
real<lower=0, upper=1> theta; // probability of success
}
model {
theta ~ beta(alpha, beta); // prior
X ~ binomial(N, theta);
}
generated quantities {
int predicted_y = bernoulli_rng(theta);
}
次に,fitさせます.
from cmdstanpy import CmdStanModel
data = {
"alpha": 2,
"beta": 18,
"N" : 43,
"X" : 11
}
model = CmdStanModel(stan_file="../../stancode/binomial_toymodel_01.stan")
fit = model.sample(data=data, seed=1212)
fit.summary()
10:28:26 - cmdstanpy - INFO - compiling stan file /home/runner/work/cmdstan_for_regression_monkey/cmdstan_for_regression_monkey/stancode/binomial_toymodel_01.stan to exe file /home/runner/work/cmdstan_for_regression_monkey/cmdstan_for_regression_monkey/stancode/binomial_toymodel_01
10:28:32 - cmdstanpy - INFO - compiled model executable: /home/runner/work/cmdstan_for_regression_monkey/cmdstan_for_regression_monkey/stancode/binomial_toymodel_01
10:28:32 - cmdstanpy - INFO - CmdStan start processing
10:28:32 - cmdstanpy - INFO - CmdStan done processing.
| lp__ |
-32.592600 |
0.021198 |
0.770842 |
-34.073300 |
-32.303900 |
-32.074400 |
1322.35 |
22039.2 |
1.00144 |
| theta |
0.206433 |
0.001319 |
0.051222 |
0.129039 |
0.203101 |
0.295836 |
1509.17 |
25152.8 |
1.00249 |
| predicted_y |
0.211750 |
0.006514 |
0.408600 |
0.000000 |
0.000000 |
1.000000 |
3934.19 |
65569.9 |
1.00000 |
Code
import plotly.figure_factory as ff
theta_posterior = fit.stan_variable("theta")
# Create distplot with curve_type set to 'normal'
fig = ff.create_distplot(
[theta_posterior],
["posterior_theta"],
show_hist=True,
bin_size=0.01,
show_rug=False,
)
# Add title
fig.update_layout(title_text="Posterior theta distribution", yaxis=dict(range=[0, 9]))
fig.show()
以上のように \(\mathbb E[\theta\vert X]\) は解析解と近しい結果が出力されます. また,\(\mathbb E[\theta\vert X] > 0.2\) となるので,事後分布に基づく政策意思決定として,\(d = 1\), つまりワクチン接種強制という結論が導かれることになります.