三角関数の加法定理

三角関数
Author

Ryo Nakagami

Published

2025-03-05

加法定理

Theorem 1 : 加法定理

\[ \begin{align} \sin (\alpha + \beta) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta\\ \cos (\alpha + \beta) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{align} \]

「咲いたコスモス，コスモス咲いた」なり「しこってこすってこすってしこって」と語呂合わせで加法定理を覚えたりしますが，ここでは加法定理を図形的に考えてみたいと思います．

Figure 1

Figure 1 のように半径 \(1\) の単位円周上に \(\angle DOB = \alpha + \beta\) となる点 \(B\) をとります． 同じく \(\angle AOD = \alpha\) となるように点をとると，\(\angle BOA = \beta\) となります．このとき，点 \(B\) の \(y\) 成分は \(\sin(\alpha + \beta)\) となります．

点 \(B\) から直線 \(OA\) 上に垂線を下ろし，その交点を \(C\) とすると \(OB = 1\) より

\[ \begin{align} BC & = \sin\beta\\ OC &= \cos\beta \end{align} \]

となることがわかります．点 \(C\) から垂線を下ろし，\(x\) 軸との交点を \(E\), \(B\) から直線 \(CE\) との交点を \(F\) とすると

\[ \begin{align} CE &= \sin \alpha\cos\beta\\ CF &= \cos\alpha\sin\beta \end{align} \]

したがって，\(CE + CF = \sin(\alpha + \beta)\) となることから

\[ \sin (\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \]

となることが図形的にわかります．同様に

\[ \begin{align} OE &= \cos\alpha\cos\beta\\ BF&= \sin\alpha\sin\beta \end{align} \]

より

\[ \cos(\alpha + \beta) = OE - BF = \cos\alpha\cos\beta - \sin\alpha\sin\beta \]

▶  ２角の差 \(\alpha - \beta\) の場合

\(\sin(-\beta) = -\sin(\beta)\) および \(\cos(-\beta) = \cos\beta\) より

\[ \begin{align} \sin (\alpha - \beta) &= \sin (\alpha + (-\beta))\\ &= \sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta)\\ &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{align} \]

同様に

\[ \begin{align} \cos (\alpha - \beta) &= \cos (\alpha + (-\beta))\\ &= \cos \alpha \cos (-\beta) - \sin \alpha \sin (-\beta)\\ &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \end{align} \]

以上より

\[ \begin{align} \sin (\alpha \pm \beta) &= \sin \alpha \cos \beta \pm \cos \alpha \sin \beta\\ \cos (\alpha \pm \beta) &= \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \end{align} \]

📘 REMARKS

\(\sin \theta\) は奇関数，\(\cos \theta\) は偶関数であることに留意すると

\[ \begin{align} \text{奇関数} \times \text{偶関数} &= \text{奇関数}\\ \text{偶関数} \times \text{偶関数} &= \text{偶関数}\\ \text{偶関数} + \text{偶関数} &= \text{偶関数}\\ \text{奇関数} + \text{奇関数} &= \text{奇関数} \end{align} \]

であるので，加法定理のRHSとLHSがそれぞれ対応していることがわかります．

オイラーの公式と加法定理

Theorem 2 : オイラーの公式

\[ \exp(i\theta) = \cos\theta + i\sin\theta \]

オイラーの公式を用いた加法定理の導出

\[ \begin{align} \exp(i(\alpha + \beta)) &= \exp(i\alpha)\exp(i\beta)\\ &= (\cos\alpha + i\sin\alpha)(\cos\beta + i\sin\beta)\\ &= \cos\alpha\cos\beta - \sin\alpha\sin\beta + i(\sin\alpha\cos\beta + \cos\alpha\sin\beta) \end{align} \]

\(\exp(i(\alpha + \beta)) = \cos(\alpha + \beta) + i\sin(\alpha + \beta)\) であることから実部と虚部の比較より

\[ \begin{align} \sin (\alpha + \beta) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta\\ \cos (\alpha + \beta) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \end{align} \]

二角の差の場合は

\[ \exp(i(\alpha - \beta))= \exp(i\alpha)\exp(-i\beta) \]

から同様に示すことが出来ます．

正接の加法定理

Proof

正弦と余弦の加法定理より

\[ \begin{align} \tan(\alpha \pm \beta) &= \frac{\sin(\alpha \pm \beta)}{\cos(\alpha \pm \beta)}\\ &= \frac{\sin \alpha \cos \beta \pm \cos \alpha \sin \beta}{\cos \alpha \cos \beta \mp \sin \alpha \sin \beta} \end{align} \]

分子と分母を \(\cos \alpha \cos \beta\) で割ると

\[ \begin{align} \tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \end{align} \]

Exercise 1

\(\tan 1^\circ\) が無理数であることを示せ

Solution

\(\tan 1^\circ\) がとある有理数 \(a\) であると仮定すると，加法定理より

\[ \tan 2^\circ = \frac{2a}{1 - a^2} \]

となり，有理数の四則演算は有理数で閉じていることから \(\tan 2^\circ\) も有理数であることがわかる．同様に \(4^\circ, 8^\circ, 16^\circ, 32^\circ\) も有理数であることがわかる．

ここで，

\[ \tan 30^\circ = \frac{\sqrt{3}}{3} \]

より \(\tan 30^\circ\) は無理数であることに着目する．一方，\(\tan 30^\circ\) は加法定理より

\[ \begin{align} \tan 30^\circ &= \tan (32^\circ - 2^\circ)\\ &= \frac{\tan 32^\circ + \tan 2^\circ}{1 + \tan 32^\circ\tan 2^\circ} \end{align} \]

このとき，\(\tan 32^\circ, \tan 2^\circ\) はともに有理数であるので， \(\tan 30^\circ\) は無理数であることと矛盾． したがって，\(\tan 1^\circ\) は無理数である．

倍角の公式とサインカーブ

Theorem 3 : 倍角の公式

\[ \begin{align} \sin 2\theta &= 2\sin\theta\cos\theta\\ \cos 2\theta &= \cos^2\theta - \sin^2\theta\\ &= 1 - 2\sin^2\theta = 2\cos^2\theta - 1\\ \tan 2\theta &= \frac{2\tan\theta}{1 - \tan^2\theta} \end{align} \]

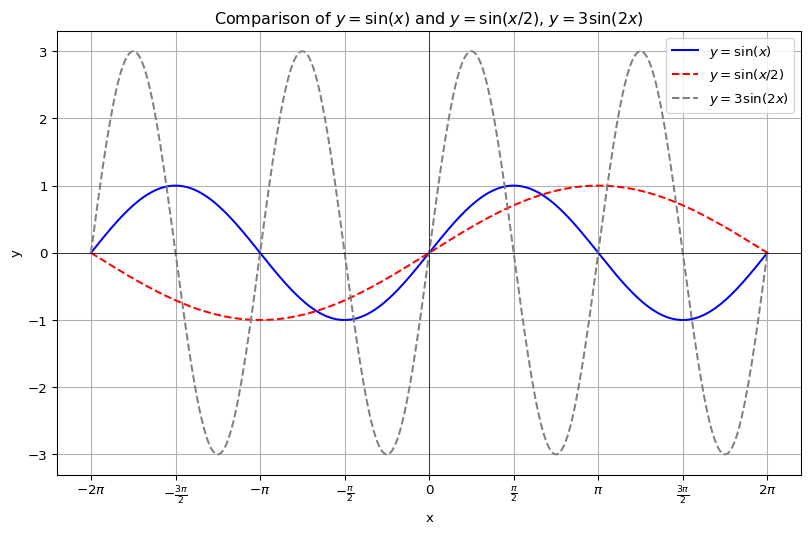
\(y = \sin x\) は振幅 \(1\) で周期 \(2\pi\) の周期関数ですが，

\[ y = \alpha\sin \beta x \quad \alpha > 0, \beta > 0 \]

と変形すると，振幅 \(\alpha\) で周期 \(\displaystyle \frac{2\pi}{\beta}\) の周期関数となります．

Code 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

# Define the x values
x = np.linspace(-2 * np.pi, 2 * np.pi, 400)

# Define the y values for both functions
y1 = np.sin(x)
y2 = np.sin(x / 2)
y3 = 3 * np.sin(2 * x)

# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x, y1, label=r"$y = \sin(x)$", color="b")
plt.plot(x, y2, label=r"$y = \sin(x/2)$", color="r", linestyle="--")
plt.plot(x, y3, label=r"$y = 3\sin(2x)$", color="gray", linestyle="--")

# Add labels, title, and legend
plt.xlabel("x")
plt.ylabel("y")
plt.title("Comparison of $y = \sin(x)$ and $y = \sin(x/2)$, $y = 3\sin(2x)$")
plt.axhline(0, color="black", linewidth=0.5)
plt.axvline(0, color="black", linewidth=0.5)
plt.legend()
plt.grid(True)

# Set x-ticks to multiples of pi
xticks = np.arange(-2 * np.pi, 2.5 * np.pi, np.pi / 2)
xtick_labels = [
    r"$-2\pi$",
    r"$-\frac{3\pi}{2}$",
    r"$-\pi$",
    r"$-\frac{\pi}{2}$",
    "0",
    r"$\frac{\pi}{2}$",
    r"$\pi$",
    r"$\frac{3\pi}{2}$",
    r"$2\pi$",
]
plt.xticks(xticks, xtick_labels)

# Show the plot
plt.show()

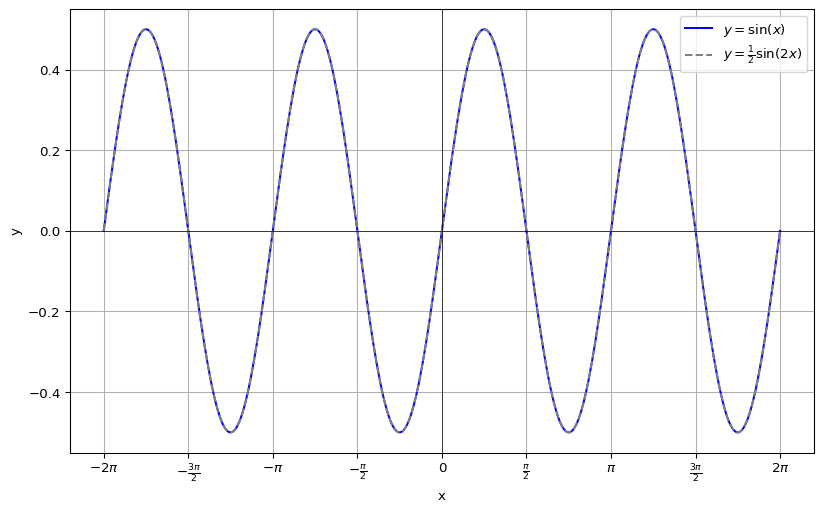
次に，\(y = \sin x \cos x\) のグラフを考えてみます．加法定理より

\[ \begin{align} \sin 2x &= \sin (x + x)\\ &= 2\sin x\cos x \end{align} \]

であることから

\[ \sin x \cos x = \frac{1}{2}\sin 2x \]

つまり，\(y = \sin x \cos x\) のグラフは振幅 \(\displaystyle \frac{1}{2}\)，周期 \(\pi\) のサインカーブとなることがわかります．

Code 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

# Define the x values
x = np.linspace(-2 * np.pi, 2 * np.pi, 400)

# Define the y values for both functions
y1 = np.sin(x) * np.cos(x)
y2 = np.sin(2 * x) /2

# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x, y1, label=r"$y = \sin(x)$", color="b")
plt.plot(x, y2, label=r"$y = \frac{1}{2}\sin(2x)$", color="gray", linestyle="--")

# Add labels, title, and legend
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(0, color="black", linewidth=0.5)
plt.axvline(0, color="black", linewidth=0.5)
plt.legend()
plt.grid(True)

# Set x-ticks to multiples of pi
xticks = np.arange(-2 * np.pi, 2.5 * np.pi, np.pi / 2)
xtick_labels = [
    r"$-2\pi$",
    r"$-\frac{3\pi}{2}$",
    r"$-\pi$",
    r"$-\frac{\pi}{2}$",
    "0",
    r"$\frac{\pi}{2}$",
    r"$\pi$",
    r"$\frac{3\pi}{2}$",
    r"$2\pi$",
]
plt.xticks(xticks, xtick_labels)

# Show the plot
plt.show()

Theorem 4 : 半角の公式

\[ \begin{align} \sin^2 \frac{\theta}{2} &= \frac{1 - \cos\theta}{2}\\ \cos^2 \frac{\theta}{2} &= \frac{1 + \cos\theta}{2}\\ \tan^2 \frac{\theta}{2} &= \frac{1 - \cos\theta}{1 + \cos\theta} \end{align} \]

Example 1

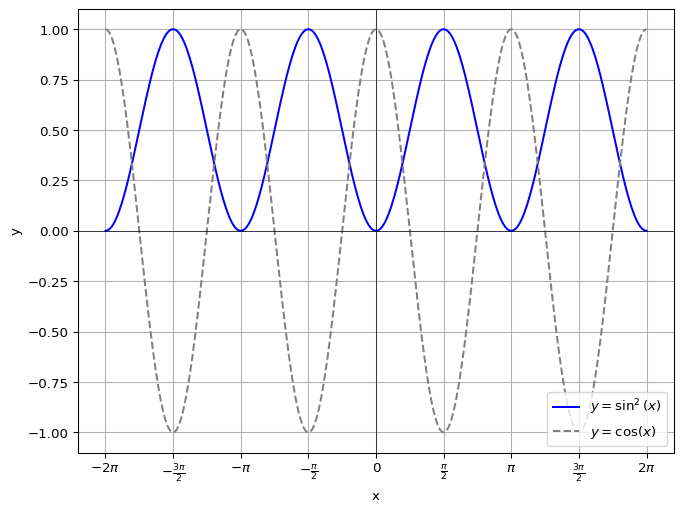
\(y = \sin^2 x\) について考えてみます．正弦関数は奇関数であるので，\(\sin^2 x\) は偶関数になるはずです．半角の公式を用いると

\[ \sin^2 x = \frac{1 - \cos 2x}{2} \]

となるので，振幅 \(\displaystyle\frac{1}{2}\), 周期 \(\pi\) のコサインカーブを \(\displaystyle\frac{1}{2}\) 平行移動したものであることがわかります．

Code 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

# Define the x values
x = np.linspace(-2 * np.pi, 2 * np.pi, 400)

# Define the y values for both functions
y1 = (1 - np.cos(2 * x))/2
y2 = np.cos(2 * x)

# Create the plot
plt.figure(figsize=(8, 6))
plt.plot(x, y1, label=r"$y = \sin^2(x)$", color="b")
plt.plot(x, y2, label=r"$y = \cos(x)$", color="gray", linestyle="--")

# Add labels, title, and legend
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(0, color="black", linewidth=0.5)
plt.axvline(0, color="black", linewidth=0.5)
plt.legend( loc='lower right',)
plt.grid(True)

# Set x-ticks to multiples of pi
xticks = np.arange(-2 * np.pi, 2.5 * np.pi, np.pi / 2)
xtick_labels = [
    r"$-2\pi$",
    r"$-\frac{3\pi}{2}$",
    r"$-\pi$",
    r"$-\frac{\pi}{2}$",
    "0",
    r"$\frac{\pi}{2}$",
    r"$\pi$",
    r"$\frac{3\pi}{2}$",
    r"$2\pi$",
]
plt.xticks(xticks, xtick_labels)


# Show the plot
plt.show()

和積の公式

Theorem 5 : 正弦関数の和積の公式

\[ \begin{align} \sin \alpha + \sin\beta &= 2 \sin \frac{\alpha+\beta}{2}\cos \frac{\alpha-\beta}{2}\\ \sin \alpha - \sin\beta &= 2 \cos \frac{\alpha+\beta}{2}\sin \frac{\alpha-\beta}{2}\\ \cos \alpha + \cos\beta &= 2 \cos \frac{\alpha+\beta}{2}\cos \frac{\alpha-\beta}{2}\\ \cos \alpha - \cos\beta &= -2 \sin \frac{\alpha+\beta}{2}\sin \frac{\alpha-\beta}{2} \end{align} \]

Proof

加法定理より

\[ \begin{align} \sin (\gamma + \delta) &= \sin\gamma \cos\delta + \cos\gamma \sin\delta\\ \sin (\gamma - \delta) &= \sin\gamma \cos\delta - \cos\gamma \sin\delta \end{align} \]

これを整理すると

\[ \begin{align} \sin (\gamma + \delta) + \sin (\gamma - \delta) &= 2\sin\gamma \cos\delta\\ \sin (\gamma + \delta) - \sin (\gamma - \delta) &= 2\cos\gamma \sin\delta \end{align} \]

ここで，\(\gamma + \delta = \alpha, \gamma - \delta = \beta\) とおくと

\[ \begin{gather} \gamma = \frac{ \alpha + \beta}{2}, \quad \delta = \frac{\alpha - \beta}{2} \end{gather} \]

となるので

\[ \begin{align} \sin \alpha + \sin\beta &= 2 \sin \frac{\alpha+\beta}{2}\cos \frac{\alpha-\beta}{2}\\ \sin \alpha - \sin\beta &= 2 \cos \frac{\alpha+\beta}{2}\sin \frac{\alpha-\beta}{2} \end{align} \]

余弦関数も同様に

\[ \begin{align} \cos (\gamma + \delta) &= \cos\gamma \cos\delta - \sin\gamma \sin\delta\\ \cos (\gamma - \delta) &= \cos\gamma \cos\delta + \sin\gamma \sin\delta \end{align} \]

であるので

\[ \begin{align} \cos (\gamma + \delta) + \cos (\gamma - \delta) &= 2\cos\gamma \cos\delta\\ \cos (\gamma + \delta) - \cos (\gamma - \delta) &= -2\sin\gamma \sin\delta \end{align} \]

から導くことができます．

Example 2

\(x + y + z = \pi\) を満たす実数 \(x, y, z\) について

\[ \sin x + \sin y + \sin z = 4 \cos\frac{x}{2}\cos\frac{y}{2}\cos\frac{z}{2} \]

が成り立ちます．LHSを式変形すると

\[ \begin{align} \sin x + \sin y + \sin z &= \sin x + \sin y + \sin (\pi - (x + y))\\ &= \sin x + \sin y + \sin (x + y)\\ &= 2\sin\frac{x+y}{2}\cos\frac{x-y}{2} + 2\sin\frac{x+y}{2}\cos\frac{x+y}{2}\\ &= 2\sin\frac{x+y}{2}\left(\cos\frac{x-y}{2} + \cos\frac{x+y}{2}\right)\\ &= 2\sin\frac{x+y}{2}\times 2\cos\frac{\frac{x-y}{2} + \frac{x-y}{2}}{2}\cos\frac{\frac{x-y}{2} - \frac{x-y}{2}}{2}\\ &=4\sin\frac{x+y}{2}\cos\frac{x}{2}\cos\frac{-y}{2}\\ &=4\sin\frac{\pi-z}{2}\cos\frac{x}{2}\cos\frac{y}{2}\\ &=4\cos\frac{z}{2}\cos\frac{x}{2}\cos\frac{y}{2} \end{align} \]

References