\((Y_i, \pmb{x}_i)\) をrandom vectorとして，\(Y_i \in \mathbb R, \pmb{x}_i \in \mathbb R^k\) とします． 線形回帰では，\((Y_i, \pmb{x}_i)\) について次のようにパラメーターに関して線形な関係があるとして回帰問題を考えます．
\[ \begin{align*} Y_i &= \pmb{x}_i^T\pmb{\beta} + \epsilon_i \quad (\epsilon_i \text{: errors}) \end{align*} \]
これを行列表現にした場合，\(\pmb{Y} = (Y_1, \cdots, Y_n)^T\), \(\pmb{X} = (\pmb{x}_1, \cdots, \pmb{x}_n)^T\) として
\[ \pmb{Y} = \pmb{X}\pmb{\beta} + \pmb{\epsilon} \]
Assumption: OLSの仮定
mutually independent and identical distribution
\[ (Y_i, \pmb{x_i^T}), i = 1, \cdots, n \text{ は i.i.d} \]
Linear model
\[ \pmb{Y} = \pmb{X}\pmb{\beta} + \pmb{\epsilon} \]
error term is conditional-mean zero
\[ \mathbb E[\epsilon_i\vert \pmb{x}_i] = 0 \]
finite moments
\[ \begin{align*} \mathbb E[Y_i^2] &< \infty\\ \mathbb E[\|\pmb{x}_i^2\|] &< \infty \end{align*} \]
Full rank condition
\(\operatorname{rank}(\pmb{X}) = k\)，つまり完全な多重共線性がない
議論の単純化のため，以下では
\[ \epsilon_1, \cdots, \epsilon_m \overset{\mathrm{iid}}{\sim} N(0, \sigma^2) \tag{27.1}\]
つまり， Homoscedasticityの仮定の下で話を進めます．
▶ \(\pmb\beta\) の推定
仮定 (2), (3) より \(\mathbb E[Y_i\vert \pmb{x}_i] = \pmb{x}_i^T\pmb{\beta}\) であるので，
\[ \pmb{\beta} = \arg\min_{b} \mathbb E[(Y_i - \pmb{x}_i^T\pmb{b})^2] \tag{27.2}\]
the joint distribution \((Y_i, \pmb{x}_i)\) は事前には知られていないので、sample analogを用いて以下のように推定します
\[ \begin{align*} \widehat{\pmb{\beta}} &= \arg\min_{b} \frac{1}{N}\sum_{i=1}^N(Y_i - \pmb{x}_i^T\pmb{b})^2\\ &= \arg\min_{b} (\pmb{Y} - \pmb{X}\pmb{\beta})^T(\pmb{Y} - \pmb{X}\pmb{\beta}) \end{align*} \]
上記について，\(b\) のFOCをとると
\[ \pmb{X}^T(\pmb{Y} - \pmb{X}\widehat{\pmb{\beta}}) = 0 \]
仮定 (5) より \(\operatorname{rank}(\pmb{X}) = k\), つまりfull rankであるので \((\pmb{X}^T\pmb{X})^{-1}\) がとれます．従って，
\[ \widehat{\pmb{\beta}} = (\pmb{X}^T\pmb{X})^{-1}(\pmb{X}^T\pmb{Y}) \tag{27.3}\]
▶ \(\widehat{\pmb{\beta}}\) の漸近分散
population \(\pmb{\beta}\) を用いてerror termを以下のように表します
\[ \begin{align*} \pmb{Y}_i &= \pmb{x}_i^T\pmb{\beta} + (\pmb{Y_i} - \pmb{x}_i^T\pmb{\beta})\\ &= \pmb{x}_i^T\pmb{\beta} + \epsilon_i \end{align*} \]
両辺に \([\pmb{X}^T\pmb{X}]^{-1}\pmb{X}^T\) をかけると Equation 27.3 より
\[ \widehat{\pmb{\beta}} = \pmb{\beta} + \left[\sum\pmb{x}_i\pmb{x}_i^T\right]^{-1}\sum \pmb{x}_i\epsilon_i \]
つぎに \(\sqrt{n}(\widehat{{\pmb{\beta}}} - \pmb{\beta})\) で漸近分散を考えると，
\[ \sqrt{n}(\widehat{{\pmb{\beta}}} - \pmb{\beta}) = n\left[\sum\pmb{x}_i\pmb{x}_i^T\right]^{-1}\frac{1}{\sqrt{n}}\sum \pmb{x}_i\epsilon_i \]
\(\mathbb E[\pmb{x}_ie_i] = 0\) であるので，\(\frac{1}{\sqrt{n}}\sum \pmb{x}_i\epsilon_i\) は location は 0であることがわかります．従って，
\[ \frac{1}{\sqrt{n}}\sum \pmb{x}_i\epsilon_i = \sqrt{n}\left\{\frac{1}{n}\sum \pmb{x}_i\epsilon_i - 0\right\}\overset{\mathrm{d}}{\to} N(0, \mathbb E[\pmb{x}_i\pmb{x}^T\epsilon_i^2]) \]
また，\(\frac{1}{n}\sum\pmb{x}_i\pmb{x}_i^T\) が \(\mathbb E[\pmb{x}_i\pmb{x}_i^T]\) に確率収束するので，スラツキーの定理とCLTにより
\[ \begin{align*} \sqrt{n}(\widehat{{\pmb{\beta}}} - \pmb{\beta}) \overset{\mathrm{d}}{\to} N(0, \mathbb E[\pmb{x}_i\pmb{x}]^{-1}\mathbb E[\pmb{x}_i\pmb{x}^T\epsilon_i^2]\mathbb E[\pmb{x}_i\pmb{x}]^{-1}) \end{align*} \]
\[ \mathbb E[\pmb{x}_i\pmb{x}^T\epsilon_i^2] = \sigma^2\mathbb E[\pmb{x}_i\pmb{x}^T] \]
が成立するので
\[ \sqrt{n}(\widehat{{\pmb{\beta}}} - \pmb{\beta}) \overset{\mathrm{d}}{\to} N(0, \sigma^2\mathbb E[\pmb{x}_i\pmb{x}]^{-1}) \]
\(\pmb{X}\) で条件付けた分散は
\[ \begin{align*} \operatorname{Var}(\widehat{\pmb{\beta}}\vert \pmb{X}) & = \mathbb E[(\pmb{X}^T\pmb{X})^{-1}\pmb{X}^T\pmb\epsilon\pmb\epsilon^T\pmb{X}(\pmb{X}^T\pmb{X})^{-1}\vert \pmb{X}]\\ &= (\pmb{X}^T\pmb{X})^{-1}\pmb{X}^T\mathbb E[\pmb\epsilon\pmb\epsilon^T\vert \pmb{X}](\pmb{X}^T\pmb{X})^{-1}\pmb{X}^T\\ &= \sigma^2(\pmb{X}^T\pmb{X})^{-1} \end{align*} \]
▶ \(\pmb{Y}\) の条件付き同時分布
Equation 27.1 より\(\pmb{Y}\) の条件付き同時確率密度は
\[ \begin{align*} p&(Y_1, \cdots, Y_n\vert \pmb{x_1}, \cdots, \pmb{x_n}, \pmb{\beta}, \sigma^2)\\ &= \prod p(Y_i\vert \pmb{x_i}, \pmb{\beta}, \sigma^2) \quad \because\text{i.i.d}\\ &= (2\pi\sigma^2)^{-n/2}\exp\{- \frac{1}{2\sigma^2}\sum_{i=1}^n (Y_i - \pmb{x}_i^T\pmb{\beta})^2\} \end{align*} \tag{27.4}\]
つまり，
\[ \{\pmb{Y} \vert \pmb{X}, \pmb{\beta}, \sigma\} \sim \operatorname{N}(\pmb{X}\pmb{\beta}, \sigma^2\pmb{I}) \]
Equation 27.4 の尤度最大化は
\[ \min\sum_{i=1}^n (Y_i - \pmb{x}_i^T\pmb{\beta})^2 \]
を解くことで得られますが，これは Equation 27.2 の問題と対応していることがわかります．
▶ \(\pmb\beta\) の事後分布の導出
\(\pmb{\beta}\) についての事前分布を
\[ \pmb{\beta} \sim \operatorname{N}(\pmb{\beta}_0, \pmb{\Sigma}_0) \]
事後分布は
\[ \begin{align*} p&(\pmb\beta\vert \pmb Y, \pmb X, \sigma^2)\\ &\propto p(\pmb Y\vert \pmb X, \pmb \beta, \sigma^2)\times p(\pmb\beta)\\ &\propto \exp\{-\frac{1}{2}(-2\pmb\beta^T\pmb X^T\pmb y/\sigma^2 + \pmb\beta^T\pmb X^T\pmb X\pmb\beta/\sigma^2) - \frac{1}{2}(-2 \pmb\beta^T\pmb\Sigma_0^{-1}\pmb\beta_0 + \pmb\beta^T\pmb\Sigma_0^{-1}\pmb\beta)\} \\ &= \exp\{\pmb\beta^T(\pmb\Sigma_0^{-1}\pmb\beta_0 + \pmb X^T\pmb Y/\sigma^2) - \frac{1}{2}\pmb\beta^T(\pmb\Sigma_0^{-1} + \pmb X^T\pmb X/\sigma^2)\pmb\beta\} \end{align*} \]
多変量正規分布を仮定しているので，以下のようにまとめることができます
\[ \begin{align*} \operatorname{Var}(\pmb\beta\vert\pmb Y, \pmb X, \sigma^2) &= (\pmb\Sigma_0^{-1} + \pmb X^T\pmb X/\sigma^2)^{-1}\\ \mathbb E[\pmb\beta\vert\pmb Y, \pmb X, \sigma^2] &= (\pmb\Sigma_0^{-1} + \pmb X^T\pmb X/\sigma^2)^{-1}(\pmb\Sigma_0^{-1}\pmb\beta_0 + \pmb X^T\pmb Y/\sigma^2) \end{align*} \tag{27.5}\]
▶ \(\sigma^2\) の事前分布
多くの正規モデルでは \(\sigma^2\) の準共役事前分布は逆ガンマ分布です． \(\gamma = 1/\sigma^2\) を観測の精度とみなし，
\[ \gamma \sim \operatorname{Ga}(v_0/2, v_0\sigma^2_0/2) \]
と事前分布を設定すると
\[ \begin{align*} p&(\gamma\vert\pmb Y, \pmb X, \pmb\beta)\\[5pt] &\propto p(\gamma)\times p(\pmb Y \vert \gamma, \pmb X, \pmb\beta)\\ &\propto \left[\gamma^{v_0/2 -1} \exp(-\gamma\times v_0\sigma^2_0/2)\right] \times \left[\gamma^{n/2}\exp(-\gamma \times \operatorname{SSR}(\pmb\beta)/2)\right]\\ &= \gamma^{(v_0+n)/2 -1} \exp(-\gamma [v_0\sigma^2_0 + \operatorname{SSR}(\pmb\beta)]/2)\\[5pt] &\text{where }\quad \operatorname{SSR}(\pmb\beta) = (\pmb Y - \pmb X\pmb\beta)^T(\pmb Y - \pmb X\pmb\beta) \end{align*} \]
これはガンマ分布とみなせるので，\(\gamma = 1/\sigma^2\) より，事後分布は
\[ \{\sigma^2\vert\pmb Y, \pmb X, \pmb\beta\} \sim \operatorname{inverse-gamma}((v_0+n)/2, [v_0\sigma^2_0 + \operatorname{SSR}(\pmb\beta)]/2) \]
従って，ベイジアンアップデートは以下のような手順で行います.
▶ Step 1: \(\pmb\beta\) の更新
\[ \pmb\beta_{(s+1)}\sim \operatorname{N}(\pmb m, \pmb V) \]
▶ Step 2: \(\sigma^2\) の更新
\[ \sigma^{2}_{(s+1)}\sim \operatorname{inverse-gamma}((v_0+n)/2, [v_0\sigma^2_0 + \operatorname{SSR}(\pmb\beta_{(s+1)})]/2) \]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from sklearn import linear_model
from regmonkey_style import stylewizard as sw
from jax import numpy as jnp, scipy as jscipy
from jax import grad
import scipy.statsdf = pd.read_stata(
"https://github.com/QuantEcon/lecture-python/blob/master/source/_static/lecture_specific/ols/maketable1.dta?raw=true"
).dropna(subset=["logpgp95", "avexpr"])
df.head()| shortnam | euro1900 | excolony | avexpr | logpgp95 | cons1 | cons90 | democ00a | cons00a | extmort4 | logem4 | loghjypl | baseco | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | AGO | 8.000000 | 1.0 | 5.363636 | 7.770645 | 3.0 | 3.0 | 0.0 | 1.0 | 280.000000 | 5.634789 | -3.411248 | 1.0 |
| 2 | ARE | 0.000000 | 1.0 | 7.181818 | 9.804219 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| 3 | ARG | 60.000004 | 1.0 | 6.386364 | 9.133459 | 1.0 | 6.0 | 3.0 | 3.0 | 68.900002 | 4.232656 | -0.872274 | 1.0 |
| 5 | AUS | 98.000000 | 1.0 | 9.318182 | 9.897972 | 7.0 | 7.0 | 10.0 | 7.0 | 8.550000 | 2.145931 | -0.170788 | 1.0 |
| 6 | AUT | 100.000000 | 0.0 | 9.727273 | 9.974877 | NaN | NaN | NaN | NaN | NaN | NaN | -0.343900 | NaN |
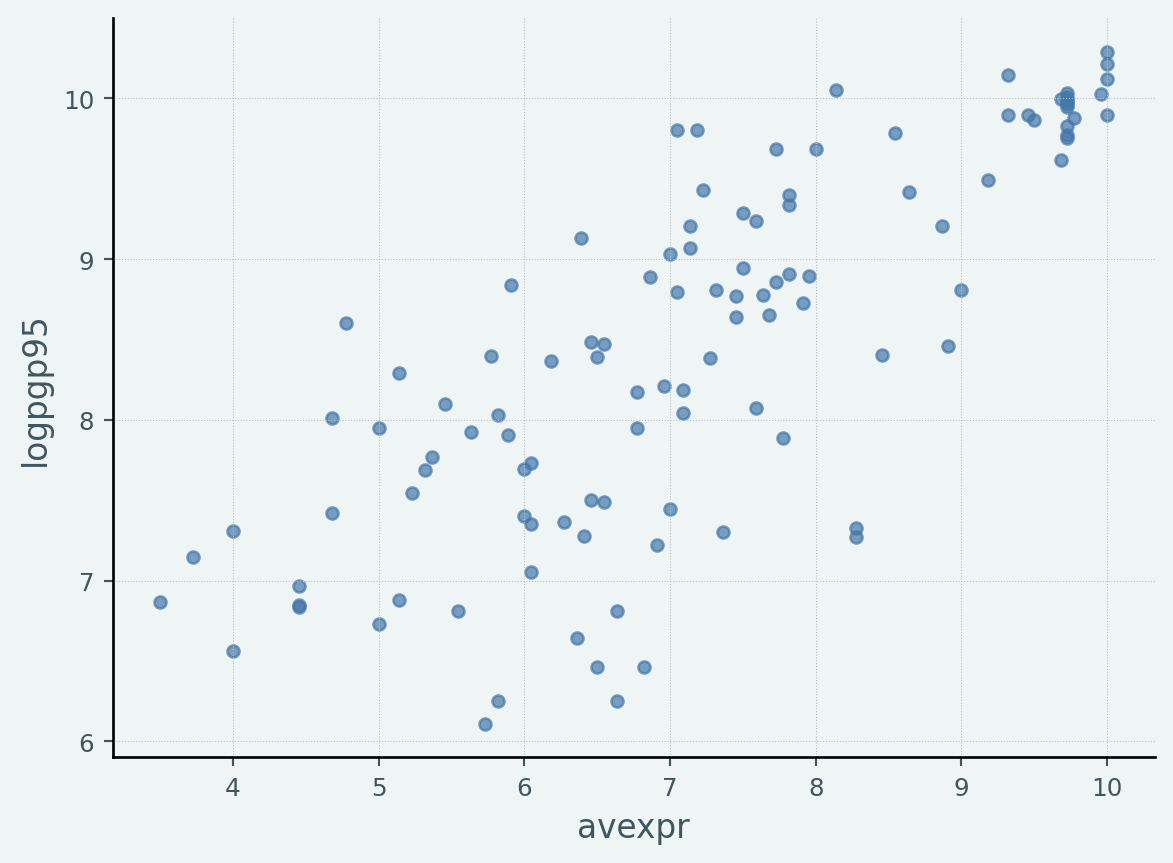
sw.set_templates("regmonkey_scatter")
df.plot(x='avexpr', y='logpgp95', kind='scatter')
plt.show()
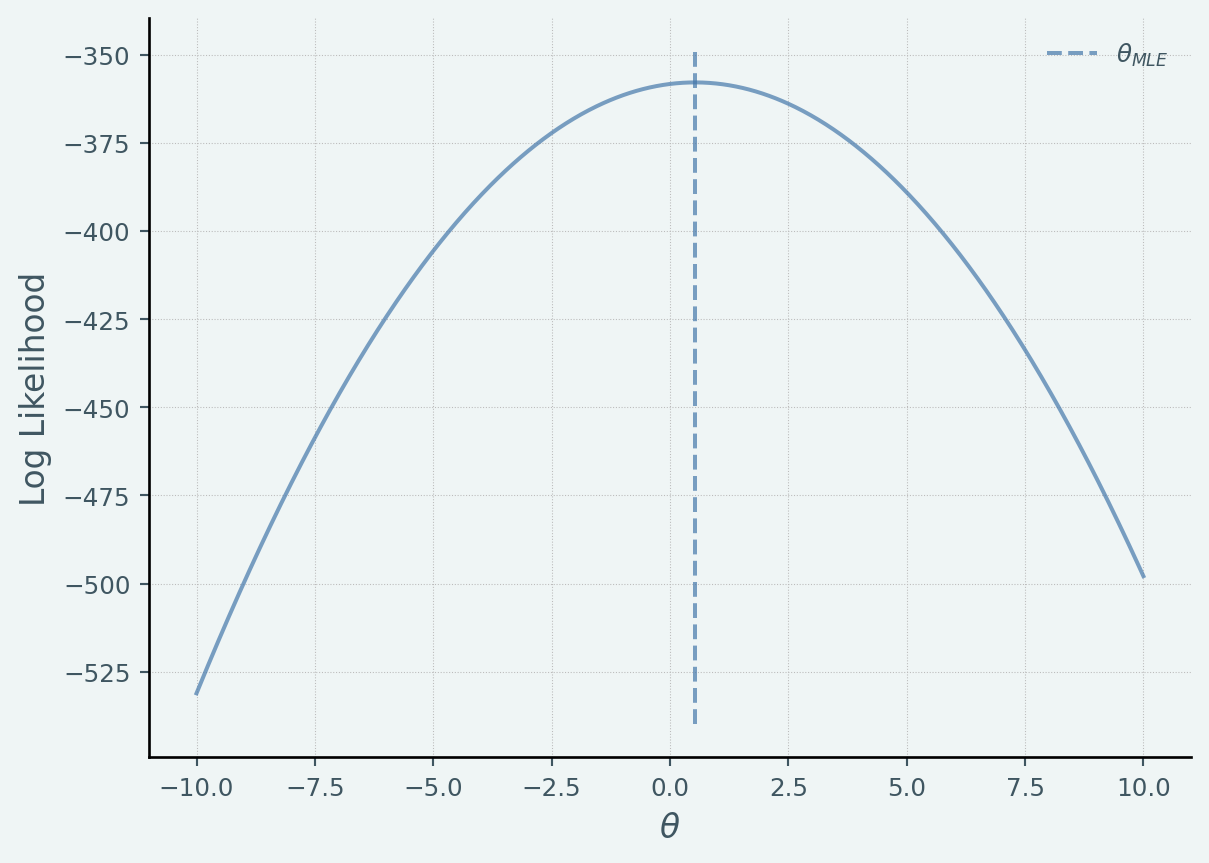
▶ MLE
def LogLikelihood(y, x, theta):
N = x.shape[0]
return np.log(scipy.stats.multivariate_normal.pdf(y.ravel(), (theta*x).ravel(), np.eye(N)*sigma_n**2))
x = df['avexpr'].values
y = df['logpgp95'].values
# FWL
x_mle = x - np.mean(x)
y_mle = y - np.mean(y)
# MLE
np.random.seed(42)
sigma_n = 10
T = np.linspace(-10,10,1000)
LL = [LogLikelihood(y_mle, x_mle, t1) for t1 in T]
fig, ax = plt.subplots()
ax.plot(T, LL)
beta_mle = np.sum(x_mle*y_mle)/np.sum(np.square(x_mle))
ax.vlines(beta_mle,*ax.get_ylim(), linestyle='--', label='$\\theta_{MLE}$')
ax.set_xlabel("$\\theta$");ax.set_ylabel("Log Likelihood");
plt.legend(bbox_to_anchor=[1,1]);
print("MLE beta: {}".format(beta_mle))MLE beta: 0.5318712592124939
▶ OLS
df_ols = df.copy()
df_ols['const'] = 1
reg_ols = sm.OLS(endog=df_ols['logpgp95'], exog=df_ols[['const', 'avexpr']], \
missing='drop')
results = reg_ols.fit()
print(results.summary()) OLS Regression Results
==============================================================================
Dep. Variable: logpgp95 R-squared: 0.611
Model: OLS Adj. R-squared: 0.608
Method: Least Squares F-statistic: 171.4
Date: Sat, 19 Oct 2024 Prob (F-statistic): 4.16e-24
Time: 10:17:22 Log-Likelihood: -119.71
No. Observations: 111 AIC: 243.4
Df Residuals: 109 BIC: 248.8
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.6261 0.301 15.391 0.000 4.030 5.222
avexpr 0.5319 0.041 13.093 0.000 0.451 0.612
==============================================================================
Omnibus: 9.251 Durbin-Watson: 1.689
Prob(Omnibus): 0.010 Jarque-Bera (JB): 9.170
Skew: -0.680 Prob(JB): 0.0102
Kurtosis: 3.362 Cond. No. 33.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.▶ Rdige
reg_l2 = sm.OLS(endog=df_ols['logpgp95'], exog=df_ols[['const', 'avexpr']], \
missing='drop')
result_l2 = reg_l2.fit_regularized(L1_wt=0., alpha=[1/2,1/2])
result_l2.paramsarray([0.55745346, 1.05775113])reg_l2 = sm.OLS(endog=y_mle, exog=x_mle, \
missing='drop')
result_l2 = reg_l2.fit_regularized(L1_wt=0., alpha=[1])
result_l2.paramsarray([0.39242079])from sklearn.linear_model import Ridge
from sklearn.linear_model import ridge_regression
coef, intercept = ridge_regression(x.reshape(-1,1), y, alpha=1.0, return_intercept=True)
print(coef, intercept)[0.5319232] 4.625326▶ bayesian regression
from IPython.display import set_matplotlib_formats
import seaborn as sns
from jax import random, vmap
import jax.numpy as jnp
from jax.scipy.special import logsumexp
import numpyro
from numpyro import handlers
from numpyro.diagnostics import hpdi
import numpyro.distributions as dist
from numpyro.infer import MCMC, NUTS
def model(x=None, y=None):
#a = numpyro.sample("a", dist.Normal(0.0, 1))
M, A = 0.0, 0.0
if x is not None:
bM = numpyro.sample("bM", dist.Normal(0.0, 1))
M = bM * x
sigma = numpyro.sample("sigma", dist.Gamma(1.0))
#mu = a + M
mu = M
numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)
# Start from this source of randomness. We will split keys for subsequent operations.
rng_key = random.PRNGKey(0)
rng_key, rng_key_ = random.split(rng_key)
kernel = NUTS(model)
num_samples = 200
mcmc = MCMC(kernel, num_warmup=100, num_samples=num_samples)
mcmc.run(
rng_key_, x=x_mle, y=y_mle
)
mcmc.print_summary()
samples_1 = mcmc.get_samples()
mean std median 5.0% 95.0% n_eff r_hat
bM 0.53 0.04 0.53 0.46 0.58 166.41 1.00
sigma 0.72 0.05 0.72 0.65 0.81 50.98 1.00
Number of divergences: 0def model(x=None, y=None):
a = numpyro.sample("a", dist.Normal(5.0, 1))
M, A = 0.0, 0.0
if x is not None:
bM = numpyro.sample("bM", dist.Normal(0.0, 1))
M = bM * x
sigma = numpyro.sample("sigma", dist.InverseGamma(1.0))
mu = a + M
numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)
# Start from this source of randomness. We will split keys for subsequent operations.
rng_key = random.PRNGKey(42)
rng_key, rng_key_ = random.split(rng_key)
kernel = NUTS(model)
num_samples = 2000
mcmc = MCMC(kernel, num_warmup=1000, num_samples=num_samples)
mcmc.run(
rng_key_, x=x, y=y
)
mcmc.print_summary()
samples_1 = mcmc.get_samples()
mean std median 5.0% 95.0% n_eff r_hat
a 4.67 0.29 4.66 4.22 5.15 647.40 1.00
bM 0.53 0.04 0.53 0.46 0.59 649.07 1.00
sigma 0.72 0.05 0.72 0.65 0.80 935.07 1.00
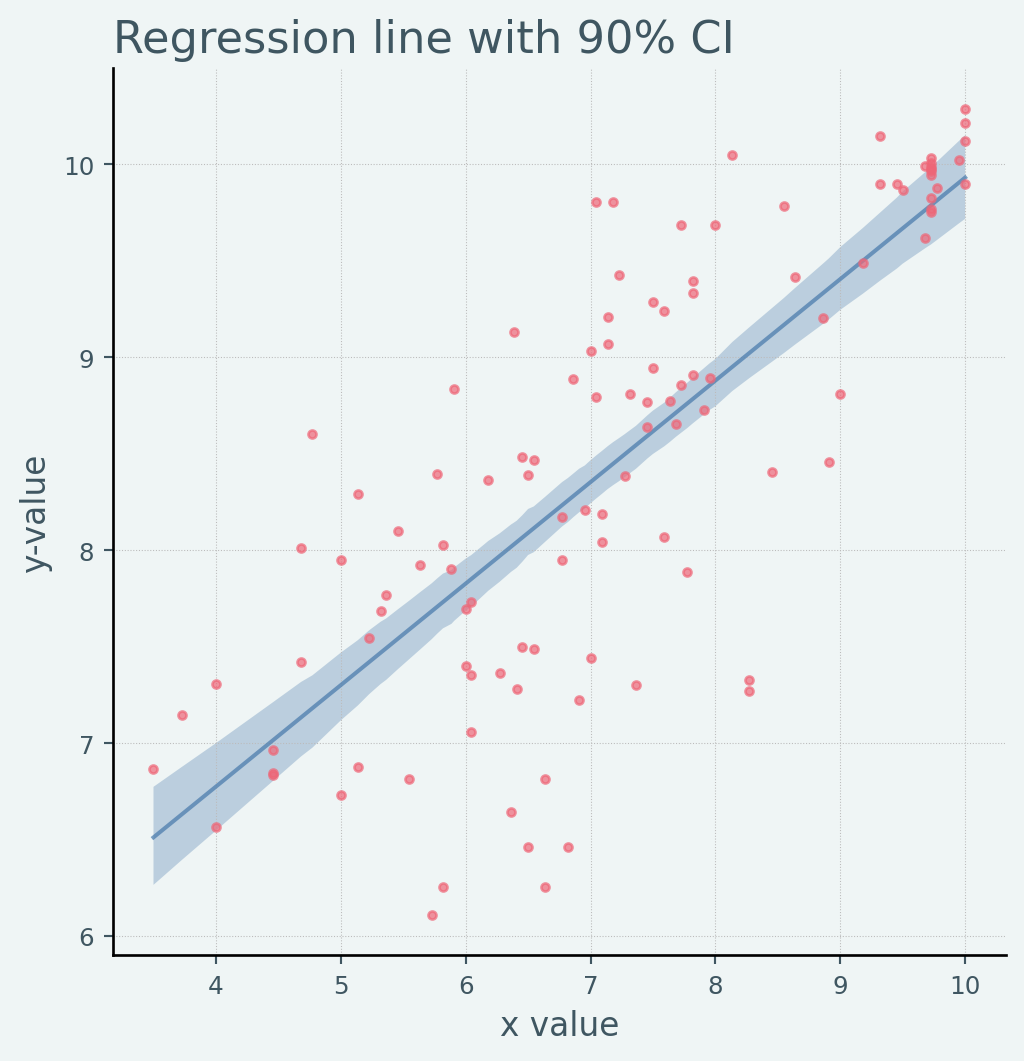
Number of divergences: 0def plot_regression(x_data, y_mean, y_hpdi, y_data):
# Sort values for plotting by x axis
idx = jnp.argsort(x_data)
x = x_data[idx]
mean = y_mean[idx]
hpdi = y_hpdi[:, idx]
y = y_data[idx]
# Plot
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 6))
ax.plot(x, mean)
ax.plot(x, y, "o")
ax.fill_between(x, hpdi[0], hpdi[1], alpha=0.3, interpolate=True)
return ax
# Compute empirical posterior distribution over mu
posterior_mu = (
jnp.expand_dims(samples_1["a"], -1)
+ jnp.expand_dims(samples_1["bM"], -1) * x
)
mean_mu = jnp.mean(posterior_mu, axis=0)
hpdi_mu = hpdi(posterior_mu, 0.9)
ax = plot_regression(x, mean_mu, hpdi_mu, y)
ax.set(
xlabel="x value", ylabel="y-value", title="Regression line with 90% CI"
);
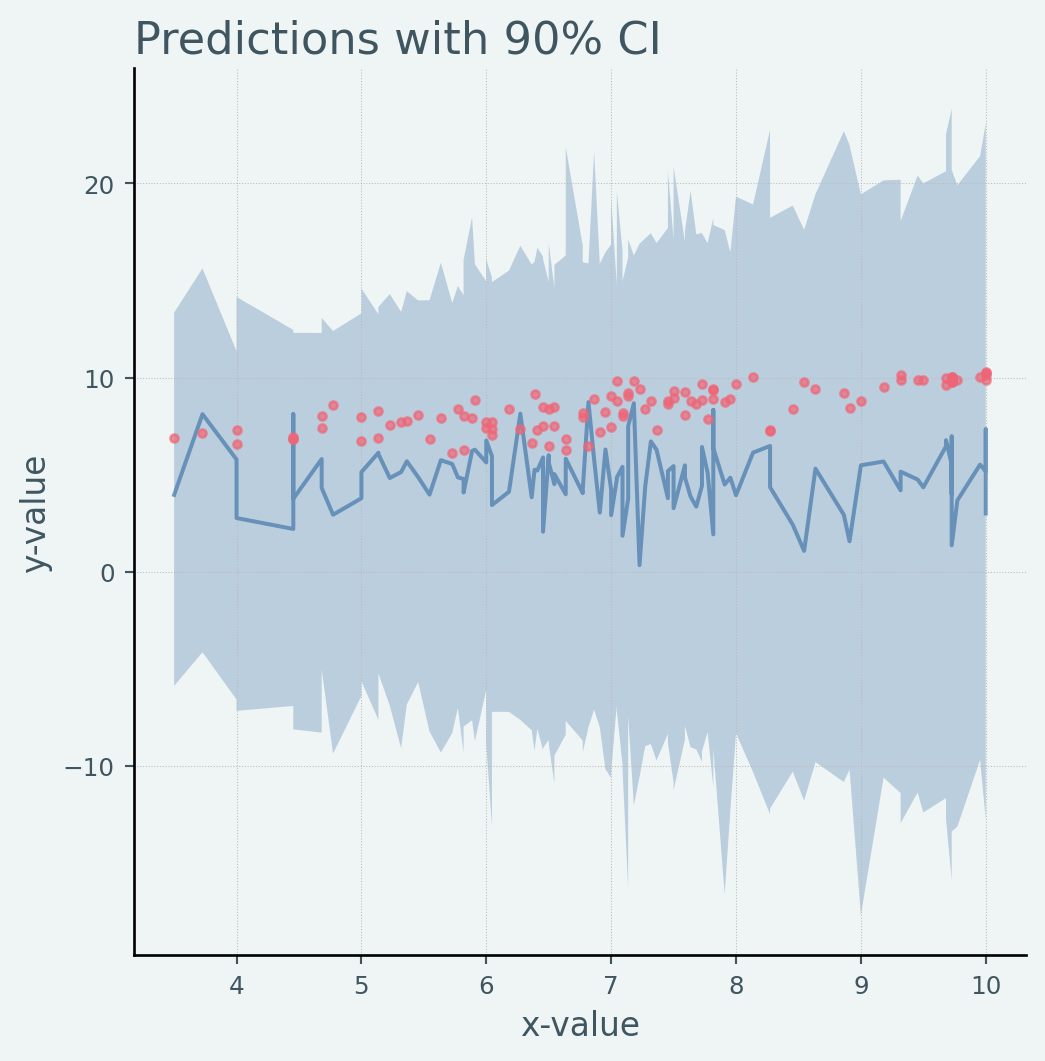
from numpyro.infer import Predictive
rng_key, rng_key_ = random.split(rng_key)
prior_predictive = Predictive(model, num_samples=100)
prior_predictions = prior_predictive(rng_key_, x)[
"obs"
]
mean_prior_pred = jnp.mean(prior_predictions, axis=0)
hpdi_prior_pred = hpdi(prior_predictions, 0.9)
ax = plot_regression(x, mean_prior_pred, hpdi_prior_pred, y)
ax.set(xlabel="x-value", ylabel="y-value", title="Predictions with 90% CI");
df_bayes = df.copy()
rng_key, rng_key_ = random.split(rng_key)
predictive = Predictive(model, samples_1)
predictions = predictive(rng_key_, x=x)["obs"]
df_bayes["Mean Predictions"] = jnp.mean(predictions, axis=0)
df_bayes.loc[:, ["shortnam", "logpgp95", "Mean Predictions"]].head()| shortnam | logpgp95 | Mean Predictions | |
|---|---|---|---|
| 1 | AGO | 7.770645 | 7.498785 |
| 2 | ARE | 9.804219 | 8.472743 |
| 3 | ARG | 9.133459 | 8.029100 |
| 5 | AUS | 9.897972 | 9.564693 |
| 6 | AUT | 9.974877 | 9.770352 |
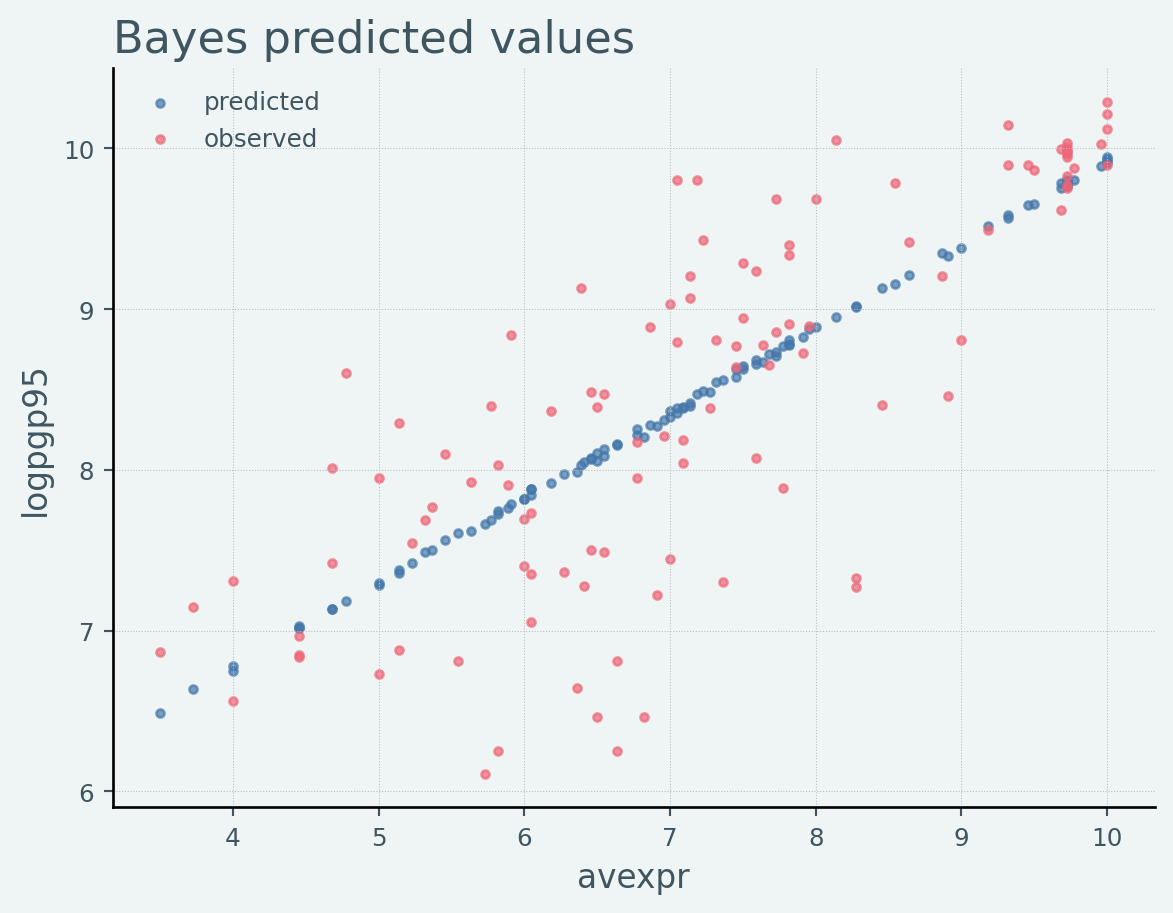
# Plot predicted values
fix, ax = plt.subplots()
ax.scatter(df_bayes['avexpr'], df_bayes["Mean Predictions"],
label='predicted')
# Plot observed values
ax.scatter(df_bayes['avexpr'], df_bayes["logpgp95"],
label='observed')
ax.legend(loc='upper left')
ax.set_title('Bayes predicted values')
ax.set_xlabel('avexpr')
ax.set_ylabel('logpgp95')
plt.show()
def log_likelihood(rng_key, params, model, *args, **kwargs):
model = handlers.condition(model, params)
model_trace = handlers.trace(model).get_trace(*args, **kwargs)
obs_node = model_trace["obs"]
return obs_node["fn"].log_prob(obs_node["value"])
def log_pred_density(rng_key, params, model, *args, **kwargs):
n = list(params.values())[0].shape[0]
log_lk_fn = vmap(
lambda rng_key, params: log_likelihood(rng_key, params, model, *args, **kwargs)
)
log_lk_vals = log_lk_fn(random.split(rng_key, n), params)
return (logsumexp(log_lk_vals, 0) - jnp.log(n)).sum()
rng_key, rng_key_ = random.split(rng_key)
print(
"Log posterior predictive density: {}".format(
log_pred_density(
rng_key_,
samples_1,
model,
x=x,
y=y,
)
)
)Log posterior predictive density: -119.95238494873047