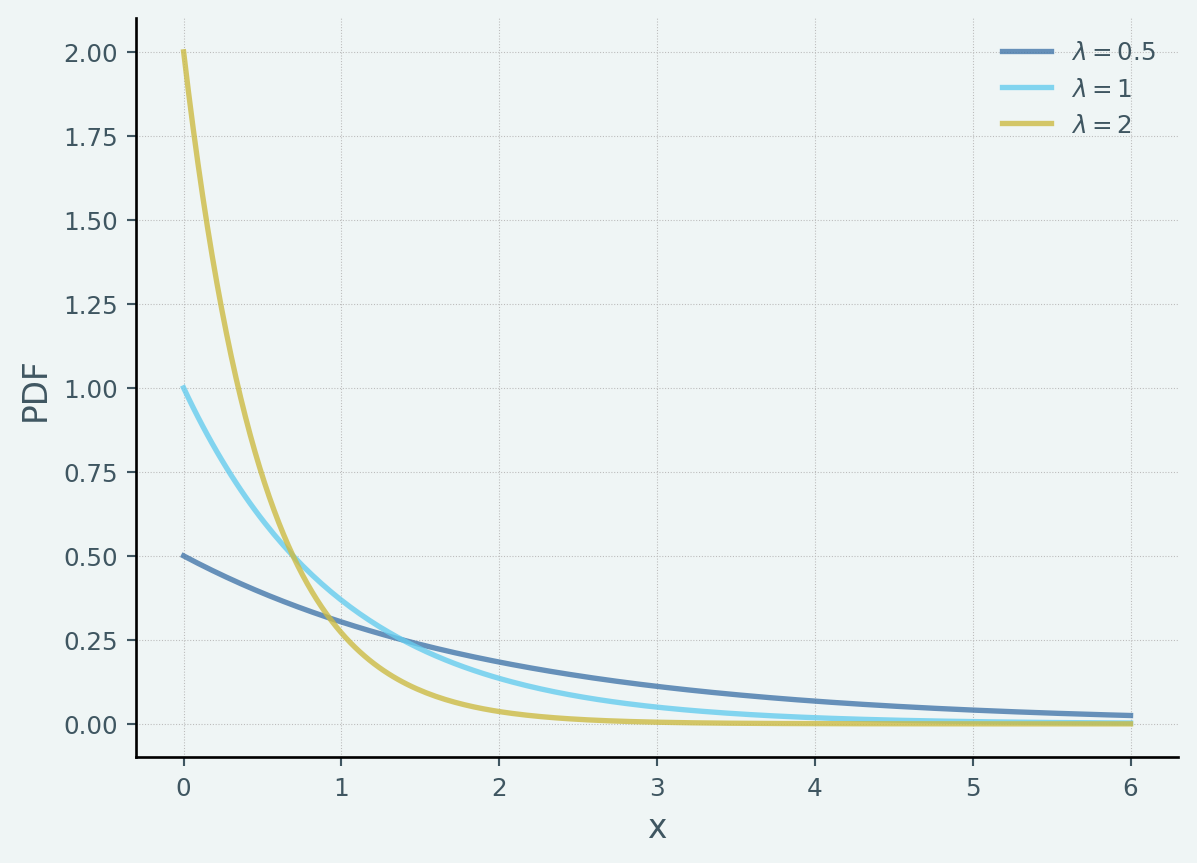
指数分布の性質
Def: 指数分布
連続確率変数 \(X\) がパラメータ \(\lambda > 0\) の指数分布に従う, \(X \sim \operatorname{Exp}(\lambda)\),のとき,その確率密度関数 \(f(x)\) は
\[
f(x) = \left\{\begin{array}{c}
\lambda \exp(-\lambda x) & (x > 0)\\
0 & \text{otherwise}
\end{array}\right.
\]
累積分布関数 \(F(x)\) は
\[
\begin{align*}
F(x)
& = \int^x_{-\infty}f(x)\,\mathrm{d}x\\
&= [1 - \exp(-\lambda x)]\mathbb 1(X >0)
\end{align*}
\]
指数分布は連続的な待ち時間分布の性質(=幾何分布の連続変数版)という特徴を持ちます.そのため後述しますが無記憶性の性質を持っています. 指数分布は,故障率が一定のシステムの偶発的な故障までの待ち時間(耐用年数や寿命)を当てはめる際に用いられたりします.
Code
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from regmonkey_style import stylewizard as sw
sw.set_templates("regmonkey_line")
fig, ax = plt.subplots()
lambda_vals = [0.5, 1, 2]
x_grid = np.linspace(0, 6, 200)
for _lambda in lambda_vals:
z = stats.expon(scale=1 / _lambda)
ax.plot(x_grid, z.pdf(x_grid), alpha=0.8, lw=2, label=f"$\lambda={_lambda}$")
ax.set_xlabel("x")
ax.set_ylabel("PDF")
plt.legend()
plt.show()
▶ 期待値の導出
\[
\begin{align*}
\mathbb E[X]
&= \int^\infty_0 x \lambda \exp(-\lambda x)\,\mathrm{d}x\\
&= \underbrace{[-x\exp(-\lambda x)]^\infty_0}_{=0} + \int^\infty_0 \exp(-\lambda x)\,\mathrm{d}x\\
&= \frac{1}{\lambda}\left[- \exp(-\lambda x)\right]^\infty_0\\
&= \frac{1}{\lambda}
\end{align*}
\]
▶ 分散の導出
\[
\begin{align*}
\mathbb E[X^2]
&= \int^\infty_0 x^2 \lambda \exp(-\lambda x)\,\mathrm{d}x\\
&= \underbrace{[-x^2\exp(-\lambda x)]^\infty_0}_{=0} + \frac{2}{\lambda}\underbrace{\int^\infty_0 x \lambda \exp(-\lambda x)\,\mathrm{d}x}_{=\mathbb E[X]}\\
&= \frac{2}{\lambda^2}
\end{align*}
\]
従って,
\[
\begin{align*}
\operatorname{Var}(X)
&= \mathbb E[X^2] - (\mathbb E[X])^2\\
&= \frac{2}{\lambda^2} - \frac{1}{\lambda^2}\\
&= \frac{1}{\lambda^2}
\end{align*}
\]
\[\tag*{\(\blacksquare\)}\]
\(\mathbb E[X] = \frac{1}{\lambda}\), \(\operatorname{Var}(x) = \frac{1}{\lambda^2}\) より, 生起までの年数が指数分布かつ希少事例(\(\lambda\) が小さい)場合,\(\mathbb [X] \pm \sigma\) が0まで伸びています. 確率が小さいことと遠い将来にしか発生しないは同じではないことがわかります.
▶ Modeの導出
最頻値(Mode)はPDF \(f_X(x)\) を最大化する \(x \in\mathcal{X}\) なので
\[
\operatorname{Mode}(X) = \arg\max_x f_X(x)
\]
\(f_X(0) = \lambda\) また \(x > 0\) の範囲で \(0 < \exp(-\lambda x) < 1\) なので,
\[
\operatorname{Mode}(X) = 0
\]
\[\tag*{\(\blacksquare\)}\]
Theorem 17.1 : Median
確率変数 \(X \sim \operatorname{Exp}(\lambda)\) について,
\[
\operatorname{Median}(X) = \frac{\log 2}{\lambda}
\]
分位点関数
\(\operatorname{Median}(X) = x^*\) としたとき,
\[
\begin{gather}
1 - \exp(-\lambda x^*) = \frac{1}{2}\\
\Rightarrow x^* = \frac{\log 2}{\lambda}
\end{gather}
\]
Theorem 17.2 : Quantile function
確率変数 \(X \sim \operatorname{Exp}(\lambda)\) について,分位点関数は
\[
Q_X(p) = \left\{
\begin{array}{rl}
-\infty \; , & \text{if} \; p = 0 \\
-\frac{\ln(1-p)}{\lambda} \; , & \text{if} \; p > 0 \; .
\end{array}\right.
\]
確率変数 \(X \sim \operatorname{Exp}(\lambda)\) のCDFを \(F_X(x)\) とすると,
\[
F_X(x) = 1 - \exp(-\lambda x)
\]
このとき分位点関数は
\[
Q_X(p) = \inf\{x\in\mathbb R\vert F_X(x) \geq p\}
\]
\(p=0\) のとき, \(Q_X(0) = -\infty\). また,\(p > 0\) のとき,
\[
Q_X(p) = F^{-1}_X(p)
\]
従って,
\[
\begin{gather}
p = 1 - \exp(-\lambda x)\\
\Rightarrow \exp(-\lambda x) = 1 - p\\
\Rightarrow x = -\frac{\log(1 - p)}{\lambda}
\end{gather}
\]
MGF
Theorem 17.3 : MGF
\(X\sim\operatorname{Exp}(\lambda)\) について,MGFは
\[
M_X(t) = \frac{\lambda}{\lambda - t}
\]
ただし,\(t < \lambda\) の範囲でのみ定義される.
\[
\begin{align*}
M_X(t) &= \int_0^{\infty} e^{tx} \cdot f_X(x) \,\mathrm{d} x\\
&= \int_0^{\infty} e^{tx}\cdot \lambda e^{-\lambda x} \mathrm{d}x\\
&= \int_0^{\infty} \lambda e^{x(t-\lambda)} \mathrm{d}x\\
&= \frac{\lambda}{t-\lambda} e^{x(t-\lambda)} \Big|_{x = 0}^{x = \infty}\\
&= \lim_{x\rightarrow \infty} \left[ \frac{\lambda}{t-\lambda} e^{x(t-\lambda)} - \frac{\lambda}{t-\lambda}\right]\\
&= \frac{\lambda}{t-\lambda} \left[ \lim_{x\rightarrow \infty} e^{x(t-\lambda)} -1 \right]
\end{align*}
\]
\(t = \lambda\) では \(M_X(t)\) が定義できないことがわかります.また,\(t > \lambda\) では
\[
\lim_{x\to\infty}e^{x(t-\lambda)}\to \infty
\]
となり,同様に定義できないことがわかります.\(t < \lambda\) においてのみ以下のようにMGFは定義できます.
\[
\begin{align*}
M_X(t) &= \frac{\lambda}{t-\lambda} \left[ \lim_{x\rightarrow \infty} e^{x(t-\lambda)} -1 \right] \\
&= \frac{\lambda}{t-\lambda} \left[ 0 - 1 \right] \\
&= \frac{\lambda}{\lambda - t}
\end{align*}
\]
ガンマ分布との関係
Theorem 17.4 ガンマ分布と指数分布
確率変数 \(X \sim \operatorname{Gam}(1, \lambda^{-1})\) は \(\operatorname{Exp}(\lambda)\) と一致する.
\(\operatorname{Gam}(a, b)\) の確率密度関数は
\[
\frac{1}{b^a\Gamma(a)}x^{a-1}\exp(-x/b)
\]
これに \(a = 1, b = \lambda^{-1}\) を代入すると
\[
\begin{align*}
\frac{1}{\lambda^{-1}\Gamma(1)}x^{1-1}\exp(-\lambda x) = \lambda\exp(-\lambda x)
\end{align*}
\]
これは指数分布 \(\operatorname{Exp}(\lambda)\) の確率密度関数と一致する.
Theorem 17.5 : 指数分布に従う確率変数の和とガンマ分布
\(\operatorname{Exp}(\lambda)\) に独立に従う確率変数 \(X_1, \cdots, X_n\) について,
\[
Z = X_1 + \cdots + X_n
\]
このとき,
\[
Z \sim \operatorname{Gam}(n, \lambda^{-1})
\]
\(Z\) についての特性関数は
\[
\begin{align*}
\phi(t) &= \left(\frac{\lambda}{\lambda - it}\right)^n\\
&= (1 - it/\lambda)^{-n}
\end{align*}
\]
従って,\(\operatorname{Gam}(n, 1/\lambda)\) の特性関数と一致する.
例として,あるシステムは5回の故障が発生すると,全面的にシステムダウンしてしまうケースを考えます. 一回の故障時間間隔 \(T_i \overset{\mathrm{iid}}{\sim} \operatorname{Exp}(1/\lambda)\) とすると,システムダウンまでの時間 \(X\) は
\[
X = T_1 + T_2 + T_3 +T_4 + T_5
\]
と表すことができ,Theorem 17.5 より
\[
X \sim \operatorname{Gam}(5, \lambda)
\]
となります.
無記憶性
Theorem 17.6 : 指数分布の無記憶性
\(s, t\) を非負の実数とし,確率変数 \(X \sim \operatorname{Exp}(\lambda)\) のとき.
\[
P(X \geq s + t\vert X \geq s) = P(X\geq t)
\]
が成立する.
\[
\begin{align*}
P(X \geq s + t\vert X \geq s)
&= \frac{P(X \geq s + t, X \geq s)}{P(X \geq s)}\\
&= \frac{P(X \geq s + t)}{P(X \geq s)}
\end{align*}
\]
\(\operatorname{Exp}(\lambda)\) の上側確率は \(P(X\geq x) = \exp(\lambda x)\) であるので,
\[
\frac{\exp(-\lambda (s + t))}{\exp(-\lambda s)} = \exp(-\lambda t) = P(X\geq t)
\]
Theorem 17.7 : 無記憶性を持つ連続型分布は指数分布のみ
\(\mathbb R_{+} = [0, \infty)\) で定義される連続型確率確率変数 \(X\) が,任意の \(s, t\geq 0\) について
\[
P(X > s + t \vert X > s) = P(X > t)
\]
を満たすとする.このとき \(X\) は指数分布に従う.
テール確率 \(S_X(t) = P(X > t), 0 \leq t < \infty\) を考えます.このとき,\(S(t)\) は
\[
\begin{gather}
S(0) = 1\\
\lim_{t\infty}S(t) = 0
\end{gather}
\]
を満たす単調非増加関数です.無記憶性の定義から
\[
\frac{S(s + t)}{S(s)} = S(t) \Rightarrow S(s + t) = S(s)S(t)
\]
両辺より \(S(s)\) を引いて \(t >0\)で割ると,
\[
\begin{align*}
\frac{S(s + t) - S(s)}{t}
&= S(s)\frac{S(t) - 1}{t}\\
&= S(s)\frac{S(t) - S(0)}{t}
\end{align*}
\]
この両辺を \(t\to 0\) と近づけると連続型確率変数なので\(S(\cdot)\) は微分可能であるので
\[
S^\prime(s) = S(s)S^\prime(0)
\]
テール確率の単調非増加性を踏まえ \(S^\prime(0) = -\lambda, (\lambda >0)\) とおくと
\[
\frac{S^\prime(s)}{S(s)} = -\lambda
\]
これを \(s\) について不定積分すると
\[
\log(S(s)) = -\lambda s + C
\]
\(S(0)=1\) より \(C= 0\). 従って, \[
S(s) = \exp(-\lambda s)
\]
従って,この確率変数の分布確率は
\[
F_X(x) = 1 - \exp(-\lambda x)
\]
となり,\(\operatorname{Exp}(\lambda)\) の分布関数と一致する.
ハザード関数
Def: ハザード関数
非負の確率変数 \(T\) のハザード関数は次のように定義される
\[
\lambda(t) = \lim_{\mathrm{d}t\rightarrow0} \frac{P\{t \le T < t + \mathrm{d}t |
T \ge t \} }{\mathrm{d}t} = \frac{f(t)}{1 - F(t)}
\]
\(t\) まで動作している条件のもとで次の瞬間に故障する確率密度を表していると解釈できます.
\[
\begin{align*}
P\{t \le T < t + dt \vert T \ge t \}
&= \frac{P\{t \le T < t + \mathrm{d}t , T \geq t\}}{P(T\geq t)}\\
&= \frac{P\{t \le T < t + \mathrm{d}t\}}{P(T\geq t)}\\
&= \frac{F(t + \mathrm{d}t) - F(t)}{1 - F(t)}
\end{align*}
\]
と展開できるので,\(\mathrm{d}t\) で割り,\(\lim_{\mathrm{d}t\to 0}\) とすることで \(\frac{f(t)}{1 - F(t)}\) が得られることがわかります.
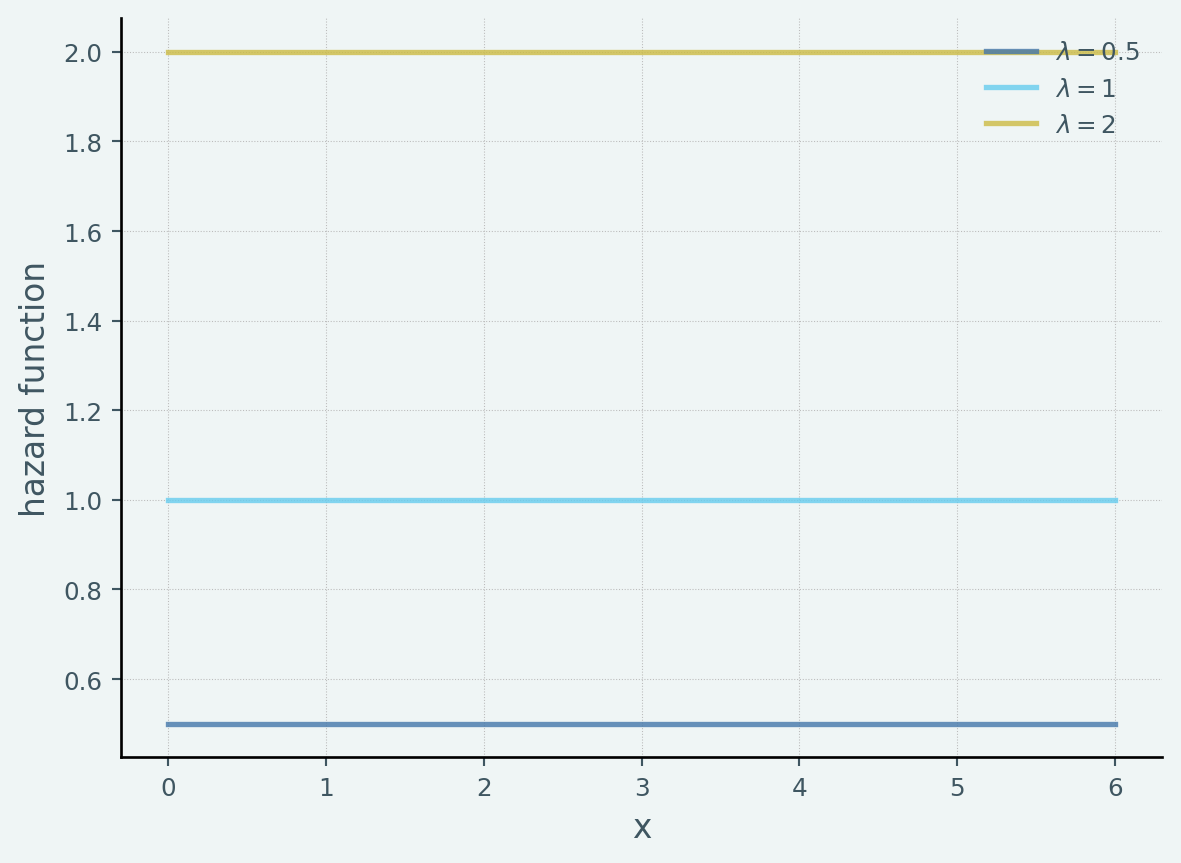
▶ 指数分布のハザード関数
\(\lambda \in \{0.2, 1, 2\}\) のパラメータを用いて各指数分布のハザード関数をplotしたのが次です.
Code
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
fig, ax = plt.subplots()
lambda_vals = [0.5, 1, 2]
x_grid = np.linspace(0, 6, 200)
for _lambda in lambda_vals:
z = stats.expon(scale=1 / _lambda)
ax.plot(x_grid, z.pdf(x_grid)/(1 - z.cdf(x_grid)), alpha=0.8, lw=2, label=f"$\lambda={_lambda}$")
ax.set_xlabel("x")
ax.set_ylabel("hazard function")
plt.legend()
plt.show()
このようにしす分布については常に \(\lambda(x) = \lambda\) で時間 \(x\) には無関係になる = 瞬間故障確率は常に一定であることがわかります.これは指数分布の無記憶性とも整合的です.
\[
\begin{align*}
\frac{f(x)}{1 - F(x)} = \frac{\lambda\exp(-\lambda x)}{\exp(-\lambda x)} = \lambda
\end{align*}
\]
のように確かめることもできます
Theorem 17.8
非負の連続型確率変数 \(X\) が \(t \geq 0\) について
\[
P(t < X \leq t + \Delta t\vert X > t) = \lambda \Delta t + o(\Delta t), \quad\lambda > 0
\]
をみたすとき, \(X\) は指数分布に従う
テール確率を \(S(x)\) と表すと
\[
\begin{align*}
P(t < X \leq t + \Delta t\vert X > t) = \frac{S(t) - S(t + \Delta t)}{S(t)}
\end{align*}
\]
従って,
\[
\frac{S(t) - S(t + \Delta t)}{S(t)}= \lambda \Delta t + o(\Delta t)
\]
両辺を \(-\Delta t\) で割ると
\[
\frac{S(t + \Delta t) - S(t)}{\Delta t}\frac{1}{S(t)}= -\lambda - \frac{o(\Delta t)}{\Delta t}
\]
\(\Delta t\to 0\) に近づけると
\[
\begin{align*}
\lim_{\Delta t\to 0}\frac{S(t + \Delta t) - S(t)}{\Delta t}\frac{1}{S(t)} &= \frac{S^\prime(t)}{S(t)}\\
\lim_{\Delta t\to 0}-\lambda - \frac{o(\Delta t)}{\Delta t} &= -\lambda
\end{align*}
\]
従って,\(S(0) = 1\) 及び単調非増加関数であるので
\[
S(t) =\exp(-\lambda t) \Rightarrow F(t) = 1 - \exp(-\lambda t)
\]
従って,\(\operatorname{Exp}(\lambda)\) の確率分布関数と一致することが分かる.