20  t分布

t 分布の性質

Def: t分布

それぞれ独立に \(Z \sim N(0, 1), X\sim\operatorname{\chi^2}(\nu)\) とするとき，

\[ T \equiv \frac{Z}{\sqrt{X/\nu}} \]

は自由度 \(m\) のt分布に従う．このとき，\(T\sim\operatorname{t}(\nu)\) と表す．

▶  確率密度関数

\(T\sim\operatorname{t}(\nu)\) のPDFは以下の形になることが知られています．

\[ \begin{align*} f_T(t) = \frac{\Gamma\left( \frac{\nu+1}{2} \right)}{\Gamma\left( \frac{\nu}{2} \right) \cdot \sqrt{\nu \pi}} \cdot \left( \frac{t^2}{\nu}+1 \right)^{-\frac{\nu+1}{2}} \end{align*} \tag{20.1}\]

Proof

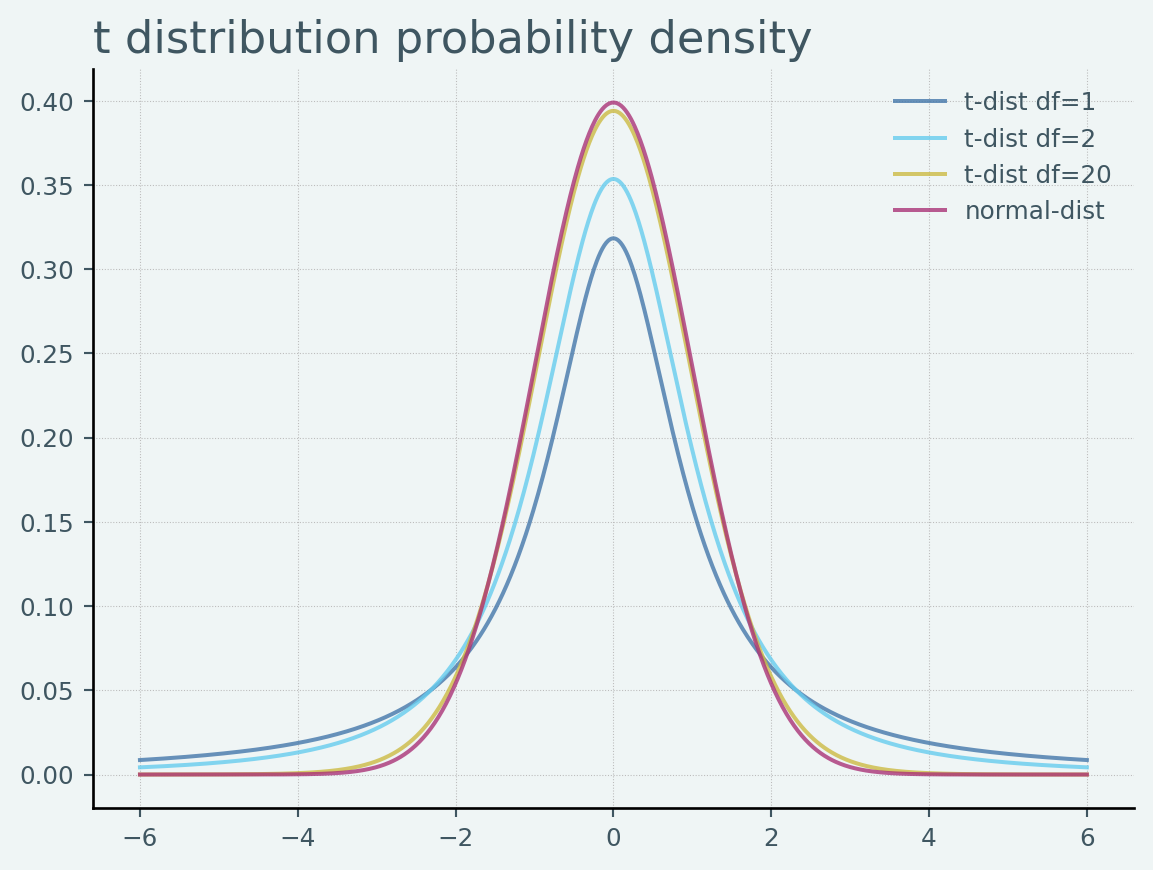
t分布の定義より，互いに独立な確率変数 \(Z \sim N(0, 1), X\sim\operatorname{\chi^2}(\nu)\) とすると

\[ T = \frac{Z}{\sqrt{X/\nu}} \]

このとき，

\[ \begin{align*} T &= \frac{Z}{\sqrt{X/\nu}}\\ W &= X \end{align*} \]

と変数変換を考える．このときJacobianは

\[ \begin{align*} Z &= T \sqrt{\frac{W}{\nu}}\\ X &= W \end{align*} \]

と表せることから

\[ \label{eq:XY-TW-jac} \begin{split} J &= \left[ \begin{matrix} \frac{\mathrm{d}X}{\mathrm{d}T} & \frac{\mathrm{d}X}{\mathrm{d}W} \\ \frac{\mathrm{d}Y}{\mathrm{d}T} & \frac{\mathrm{d}Y}{\mathrm{d}W} \end{matrix} \right] = \left[ \begin{matrix} \sqrt{\frac{W}{\nu}} & \frac{T}{2 \nu \sqrt{W/\nu}} \\ 0 & 1 \end{matrix} \right] \\ \lvert J \rvert &= \sqrt{\frac{W}{\nu}} \; . \end{split} \]

したがって，\(T, W\) についての同時確率密度関数は

\[ \begin{align*} f_{T,W}(t,w) &= f_{Z,X}(z,x) \cdot \lvert J \rvert \\[5pt] &= f_Z(z)f_X(x) \cdot \lvert J \rvert \\[5pt] &= \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{t^2w/\nu}{2}\right) \frac{1}{\Gamma(\nu/2)2^{v/2}}w^{\nu/2-1}\exp(-w/2) \sqrt{w/\nu}\\[5pt] &= \frac{1}{\sqrt{2\pi\nu}\Gamma(\nu/2)2^{\nu/2}}w^{\frac{\nu+1}{2}-1}\exp\left(-\frac{w}{2}(t^2/\nu + 1)\right) \end{align*} \]

これを用いて周辺密度関数を計算すれば良いので

\[ \begin{align*} f_T(t) &= \int_{0}^{\infty} f_{T,W}(t,w) \, \mathrm{d}w \\ &= \frac{1}{\sqrt{2 \pi \nu} \cdot \Gamma\left( \frac{\nu}{2} \right) \cdot 2^{\nu/2}} \cdot \int_{0}^{\infty} w^{\frac{\nu+1}{2}-1} \cdot \mathrm{exp}\left[ -\frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) w \right] \, \mathrm{d}w \\ &= \frac{1}{\sqrt{2 \pi \nu} \cdot \Gamma\left( \frac{\nu}{2} \right) \cdot 2^{\nu/2}} \cdot \frac{\Gamma\left( \frac{\nu+1}{2} \right)}{\left[ \frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) \right]^{(\nu+1)/2}} \cdot \int_{0}^{\infty} \frac{\left[ \frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) \right]^{(\nu+1)/2}}{\Gamma\left( \frac{\nu+1}{2} \right)} \cdot w^{\frac{\nu+1}{2}-1} \cdot \mathrm{exp}\left[ -\frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) w \right] \, \mathrm{d}w \end{align*} \]

このとき，

\[ \int_{0}^{\infty} \frac{\left[ \frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) \right]^{(\nu+1)/2}}{\Gamma\left( \frac{\nu+1}{2} \right)} \cdot w^{\frac{\nu+1}{2}-1} \cdot \mathrm{exp}\left[ -\frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) w \right] \, \mathrm{d}w = 1 \]

はガンマ分布の密度関数と考えることができるので

\[ \begin{align*} f_T(t) &= \frac{1}{\sqrt{2 \pi \nu} \cdot \Gamma\left( \frac{\nu}{2} \right) \cdot 2^{\nu/2}} \cdot \frac{\Gamma\left( \frac{\nu+1}{2} \right)}{\left[ \frac{1}{2}\left( \frac{t^2}{\nu}+1 \right) \right]^{(\nu+1)/2}} \\ &= \frac{\Gamma\left( \frac{\nu+1}{2} \right)}{\Gamma\left( \frac{\nu}{2} \right) \cdot \sqrt{\nu \pi}} \cdot \left( \frac{t^2}{\nu}+1 \right)^{-\frac{\nu+1}{2}} \end{align*} \]

import numpy as np
from scipy.stats import t
from scipy.stats import norm
import matplotlib.pyplot as plt
from regmonkey_style import stylewizard as sw

sw.set_templates("regmonkey_line")
fig, ax = plt.subplots(1, 1)

ddof = [1, 2, 20]
x = np.linspace(-6, 6, 1000)

for df in ddof:
    ax.plot(x, t.pdf(x, df), label= f't-dist df={df}', alpha=0.8)
ax.plot(x, norm.pdf(x), label= f'normal-dist', alpha=0.8)

ax.set_title("t distribution probability density")
ax.legend()
plt.show()

t分布は，標準正規分布の代用品的な位置づけをされるときがありますが，正規分布と同様に密度関数は \(x=0\) について対称です．また，上図のように自由度 \(m\) が大きくなればなるほど正規分布に近づいていくという性質もあります．

期待値

Theorem 20.1

自由度 \(\nu\) の標準的なスチューデントのt分布に従う確率変数 \(X\) の期待値は \(\nu>1\) の場合にのみ定義され

\[ \mathbb E[X] = \left\{\begin{array}{cc} 0 & (n > 1)\\ \text{not defined} & \text{otherwise} \end{array}\right. \]

Proof

\[ \begin{align*} \mathbb E[X] &= \int_{-\infty}^\infty xf_X(x) \,\mathrm{d}x\\ &= \int_{-\infty}^0 xf_X(x) \,\mathrm{d}x + \int_{0}^\infty xf_X(x) \,\mathrm{d}x\\ &= -\int_{\infty}^0 (-t)f_X(-t) \,\mathrm{d}t + \int_{0}^\infty xf_X(x) \,\mathrm{d}x\\ &= -\int^{\infty}_0 tf_X(-t) \,\mathrm{d}t + \int_{0}^\infty xf_X(x) \,\mathrm{d}x \end{align*} \]

このとき，\(\int_{0}^\infty xf_X(x) \,\mathrm{d}x\) が定義できるならば，\(y=0\) 軸との対称性より \(\mathbb E[X] = 0\) といえます． 条件を確かめてみると， \(c = \frac{\Gamma\left( \frac{\nu+1}{2} \right)}{\Gamma\left( \frac{\nu}{2} \right)}\) とおくと

\[ \begin{align*} \int_{0}^\infty xf_X(x) \,\mathrm{d} &= \lim_{u\to\infty}\int^u_0 xc\left(1 + \frac{x^2}{n}\right)^{-\frac{n+1}{2}}\,\mathrm{d}x\\ &= c \lim_{u\to\infty}\left[-\frac{n}{n-1}\left(1 + \frac{x^2}{n}\right)^{-\frac{n-1}{2}}\right]^u_0\\ &= -\frac{cn}{n-1}\left\{\lim_{u\to\infty}\left(1 + \frac{u^2}{n}\right)^{-\frac{n-1}{2}} -1\right\} \end{align*} \]

したがって，\(n > 1\) のときにfiniteになる = 定義されることがわかります．

標準コーシー分布との関係

Def: 標準コーシー分布

確率変数 \(X\) が標準コーシー分布に従うとき，その確率密度関数 \(f_X(x)\) は

\[ f_x(x) = \frac{1}{\pi}\frac{1}{x^2+1} \]

と表される．

Equation 20.1 に対して \(\nu = 1\) を代入すると

\[ \begin{align*} f_T(t) &= \frac{\Gamma\left( \frac{1+1}{2} \right)}{\Gamma\left( \frac{1}{2} \right) \cdot \sqrt{1 \pi}} \cdot \left( \frac{t^2}{1}+1 \right)^{-\frac{1+1}{2}}\\ &= \frac{1}{\sqrt{\pi}\sqrt{\pi}}\frac{1}{t^2+1}\\ &= \frac{1}{\pi}\frac{1}{t^2+1}\ \end{align*} \]

となるので，自由度 1 のt分布がコーシー分布と一致することがわかります．

Refernces

• LibreTexts Statistics > The Student t Distribution