コルモゴロフ・スミルノフ検定の性質
\(X_1,\cdots, X_n\) を独立に分布関数 \(F(x)\) に従う確率変数とします.この確率変数が特定の分布関数 \(F_0(x)\) に従うかを検定する問題を考えます:
\[
H_0: F(x) = F_0(x), H_1: \exists x_0 \in \mathbb R \text{ such that }F(x) \neq F_0(x)
\]
この問題の検定統計量として
\[
D_n = \sup_{x} \vert F_n(x) - F_0(x)\vert
\]
を用いた検定をコルモゴロフ・スミルノフ検定といいます.\(F_n(x)\) は経験分布関数です.
Example 22.1
確率変数 \(X \sim \operatorname{U}(0,1)\) を \(Y = -log(X)\) と変数変換すると
\[
Y \sim \operatorname{Exp}(1)
\]
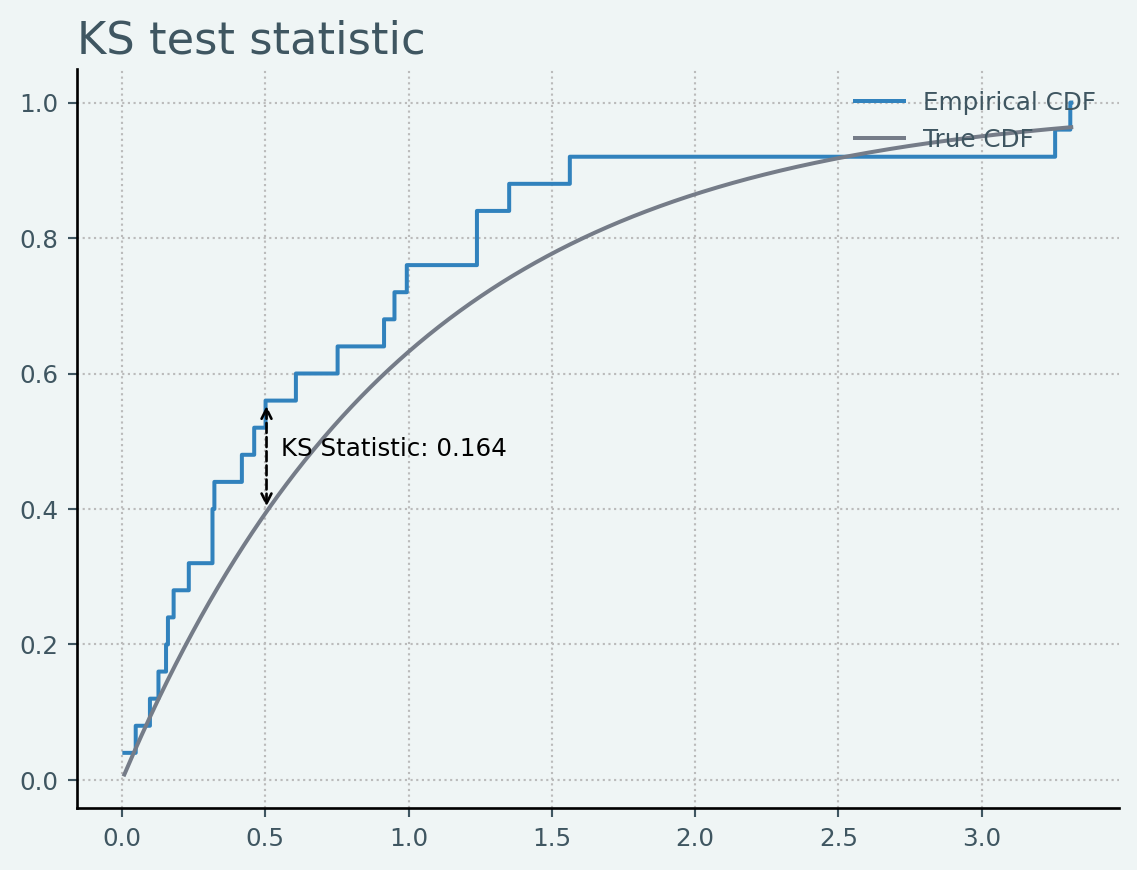
に従います.25個の標準一様分布に従う乱数を発生させ,それに基づいてKS test statisticを計算すると以下のようになります.
Code
import numpy as np
from statsmodels.distributions.empirical_distribution import ECDF
from scipy import stats
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
from regmonkey_style.config import CONFIG
from regmonkey_style import stylewizard as sw
sw.set_templates("regmonkey_twoline")
np.random.seed(2222)
# DGP
N = 25
sample = -np.log(np.random.uniform(0, 1, N))
ecdf = ECDF(sample)
x = np.linspace(min(sample), max(sample), 1000)
true_cdf = stats.expon.cdf(x)
ecdf_values = ecdf(x)
# compute statistic
sup_idx, ks_statistic = np.argmax(np.abs(true_cdf - (ecdf_values))), np.max(
np.abs(true_cdf - (ecdf_values))
)
sup_x = x[sup_idx]
fig, ax = plt.subplots()
ax.step(x, ecdf_values, label="Empirical CDF")
ax.plot(x, true_cdf, label="True CDF")
ax.annotate(
"",
xy=(sup_x, min(stats.expon.cdf(sup_x), ecdf(sup_x))),
xytext=(sup_x, max(stats.expon.cdf(sup_x), ecdf(sup_x))),
arrowprops=dict(
arrowstyle="<->", color="black", linestyle="dashed"
),
)
ax.text(
sup_x + 0.05,
(true_cdf[sup_idx] + ecdf_values[sup_idx]) / 2,
f"KS Statistic: {ks_statistic:.3f}",
color="black",
ha="left"
)
ax.set_title("KS test statistic")
ax.legend()
plt.show()
scipy.stats.ks_1samp でexactにテストをしてみると
stats.ks_1samp(sample, stats.expon(0).cdf, method='exact')
KstestResult(statistic=np.float64(0.16519761568776414), pvalue=np.float64(0.45428250331574216), statistic_location=np.float64(0.5022002367852737), statistic_sign=np.int8(1))
Def: 経験分布関数
\(n\) 個の実数値データ \(D = \{x^{(i)}\in\mathbb R\vert i=1,\cdots, n\}\) が与えられたとき,経験分布 \(\operatorname{Emp}(D)\) の確率関数 \(f_n(x)\) は次のように定義される
\[
\begin{gather}
f_n(x) = \frac{1}{n}\sum_{i=1}^n\delta(x - x^{(i)})\\
\text{where }\delta(\cdot) \text{ : Dirac delta function}
\end{gather}
\]
累積分布関数(経験分布関数) \(F_X(x)\) は次のように定義される
\[
\begin{align*}
F_n(x)
&= \frac{1}{n}\sum_{i=1}^n\int^x_{-\infty}\delta(z - x^{(i)})\,\mathrm{d}z\\
&= \frac{1}{n}\mathbb 1(x^{(i)\leq x})
\end{align*}
\]
LLN(大数の法則)より,任意の \(x\in\mathbb R\) について,
\[
F_n(x) \to \mathbb E \mathbb 1(X_i \leq x) = P(X_i\leq x) = F(x)
\]
が成立します.次に,KS Testの統計量が帰無仮説で設定した \(F\) に依存しないことを示します.
Theorem 22.1
\(F(x)\) が連続のとき,
\[
\sup_{x\in\mathbb R} \vert F_n(x) - F(x)\vert
\tag{22.1}\]
の分布は \(F\) に依存しない.
累積分布関数 \(F\) の逆関数を次のように定義します
\[
F^{-1}(y) = \min \{x: F(x)\leq y\}
\]
\(F^{-1}\) を用いて Equation 22.1 を次のように変形します
\[
\begin{align*}
P(\sup_{x\in\mathbb R} \vert F_n(x) - F(x)\vert \leq t)
= P(\sup_{y\in [0, 1]} \vert F_n(F^{-1}(y)) - y\vert \leq t)
\end{align*}
\]
経験分布関数 \(F_n\) について
\[
\begin{align*}
F_n(F^{-1}(y))
&= \frac{1}{n}\sum \mathbb 1(X_i \leq F^{-1}(y))\\
&= \frac{1}{n}\sum \mathbb 1(F(X_i) \leq y)
\end{align*}
\]
従って,
\[
P(\sup_{y\in [0, 1]} \vert F_n(F^{-1}(y)) - y\vert \leq t)
= P\left(\sup_{y\in [0, 1]} \left\vert \frac{1}{n}\sum \mathbb 1(F(X_i) \leq y) - y\right\vert \leq t\right)
\]
任意の分布の累積分布関数は標準一様分布に従うので,
\[
F(X_i) \sim \operatorname{U}(0, 1)
\]
\(U_i = F(X_i) \ \ \text{for } i \in \{1, \cdots, n\}\) とすると,
\[
P(\sup_{y\in [0, 1]} \vert F_n(F^{-1}(y)) - y\vert \leq t)
= P\left(\sup_{y\in [0, 1]} \left\vert \frac{1}{n}\sum \mathbb 1(U_i \leq y) - y\right\vert \leq t\right)
\]
以上より, Equation 22.1 の分布は \(F\) に依存しないことが示されました.
ここからKS Test統計量を統計的仮説検定のフレームワークに乗せるためには,得られた統計量の値が \(H_0\) の下でどのように評価することができるのか?を知る必要があります. 固定された \(x\) においてCLTより以下のことがわかります
\[
\sqrt{n}(F_n(x) - F(x)) \overset{\mathrm{d}}{\to} N\big(0, F(x)(1 - F(x))\big)
\]
これを用いて
\[
\sqrt{n}\sup \vert F_n(x) - F(x)\vert
\]
が収束する分布を次に確認します.
Theorem 22.2 : KS統計量の収束分布
\[
P\big(\sqrt{n}\sup_{x\in\mathbb R} \vert F_n(x) - F(x)\vert \leq t\big) \overset{\mathrm{d}}{\to} H(t)
\]
\(H(t)\) はKolmogorov-Smirnov分布でその累積分布関数は以下の形になります
\[
F_H(t) = 1 - 2\sum_{i=1}^\infty (-1)^{i-1}\exp(-2i^2t)
\]
\(F_0\) を帰無仮説で設定した分布としたとき,十分大きい \(n\) のもとで \(F_n\) は \(F\) に収束するので検定統計量に基づく判断は,十分小さい \(\delta\) を選び
\[
\sup_x \vert F_n(x) - F_0(x)\vert > \delta
\]
これで判断できれば良いとなります.これに対して,\(\sqrt{n}\) を両辺に乗じると
\[
D_n = \sqrt{n}\sup_x \vert F_n(x) - F_0(x)\vert > \sqrt{n}\delta
\]
もし \(H_0\) が不成立ならば
\[
D_n > \sqrt{n}\delta \to \infty \quad\text{as } n \to \infty
\]
従って,Decision ruleは
\[
\delta =
\left\{\begin{array}{cc}
H_0 & D_n \leq c\\
H_1 & D_n > c\\
\end{array}\right.
\]
このDecision ruleのもとでの有意水準 \(\alpha\) は
\[
\alpha = P(\delta \neq H_0\vert H_0) = P(D_n > c \vert H_0) \approx 1 - H(c)
\]
\(H(c)\) を計算するのは困難な場合が多いので,有意水準 \(\alpha\) に対応した \(c\) の数値として
\[
\begin{align*}
x_\alpha &= [-(1/2)\log(\alpha/2)]^{1/2} \quad \text{(棄却点)}\\
c &= x_\alpha/\sqrt{n}
\end{align*}
\]
として計算されます.
また,標本におけるKS統計量の計算も
\[
D = \max_{1 \le i \le N} \left( F(Y_{i}) -
\frac{i-1} {N}, \frac{i}{N} - F(Y_{i}) \right)
\]
として標本における各点における帰無仮説の分布との距離のupper boundをベースに計算されます.
コルモゴロフ・スミルノフ検定の注意点
KS Testは分布によらない推測法というメリットはありますが,帰無仮説の分布を指定する必要がありますし,また次の注意点があります.
- 連続型確率分布の検定のみしか使えない
- テール部分と比べ分布の中心付近での距離に対してsensitive = テール分布の違いには鈍感
- 帰無仮説の分布をlocation, shapeなどのパラメータを全て指定しないと,同じ分布族を帰無仮説に指定していても棄却されてしまう
このような注意点に加え, Anderson-Darling testやCramer Von-Mises testといった改良型の検定手法があるので,KS Testはあまり利用されることはありません.