30  Bias and Variance

Bias and Variance in Prediction

未知のパラメーターの推定量に焦点を当てた統計的推定とことなり，教師あり機械学習の予測では \(x\) が与えられたときに \(y\) を良く予測できる関数 \(h\)

\[ \begin{align*} &y = h(x) + \epsilon\\ &\text{where } \mathbb E[\epsilon \vert x] = 0 \end{align*} \]

を学習することを目指します．予測関数の良さについては決定理論(decision theory)で議論されるものですが，一旦L2距離で良さを判断する場合，良い関数は \(\mathbb E[y\vert x]\) となります．この関数の学習を目指して，

\[ D = \{x^{(i)}, y^{(i)}\}_{i=1}^n \]

をtraining datasetとして，\(\hat f_D\) という関数を構築したとします．母集団からランダムサンプリング された \(S\) にはノイズ \(\epsilon_i\) が含まれており，\(S\) を用いて学習した \(\hat f_D\) は確率的に変動する側面があります．その上で同じ母集団からi.i.dでサンプリングされた未知のデータセット \(\{x^{*}, y^{*}\}\) においても \(x\) を特徴量として用いることで 精度良く \(y\) を予測することができること = 汎化誤差(generalization error)が小さい \(\hat f_D\) が望ましい予測関数となります．

汎化誤差を \(y\) と \(\hat f_D\) のL2距離と考え，\(x^*\) で条件づけた場合，

\[ \begin{align*} &\operatorname{MSE}(\hat f_D)\\[5pt] &= \mathbb E_{D, y^*}[(y^* - \hat f_D(x^*))^2]\\[5pt] &= \mathbb E_{D, y^*}[(h(x^*) + \epsilon - \hat f_D(x^*))^2]\\[5pt] &= \mathbb E_{y^*}[\epsilon^2] + \mathbb E_D[(h(x^*) -\hat f_D(x^*))^2]\\[5pt] &= \mathbb E_D[\epsilon^2] + \underbrace{\mathbb E_D[h(x^*) -\hat f_D(x^*)]^2}_{=\text{bias and constant}} + \operatorname{Var}(h(x^*) -\hat f_D(x^*))\\[5pt] &= \underbrace{\operatorname{Var}(\epsilon)}_{\text{irreducible error}} + \text{Bias}(\hat f_D)^2 + \operatorname{Var}(\hat f_D) \end{align*} \tag{30.1}\]

上式の第３項のVarianceは予測関数 \(f\) の特定のtraing data集合 \(D\) の選び方に関する敏感さを表していると解釈されます．

▶  regession with gauss basis function

上記の議論を踏まえると，Bias, Varianceをバランス良く小さくするモデルがMSEの意味で良い予測モデルということになります．

経験則的に，柔軟性のある複雑なモデルはBiasは小さいがVarianceが大きく，逆に柔軟性の低いモデルはBiasが大きいがVarianceが小さいことが知られています．

以下の例では，

\[ \begin{align*} y_i &= \sin(2\pi x_i) + \epsilon_i\\ \epsilon_i &\overset{\mathrm{iid}}{\sim} N(0, 0.5^2)\\ x_i &\overset{\mathrm{iid}}{\sim} \operatorname{Uniform}(0, 1) \end{align*} \]

というData Generating Processのもとで \(N_{train} = 25\) からなるsampleを生成し，そのsample生成を100回繰り返す処理を考えます．つまり，

• それぞれのsample sizeは \(N_{train} = 25\)
• sample数は \(L = 100\)

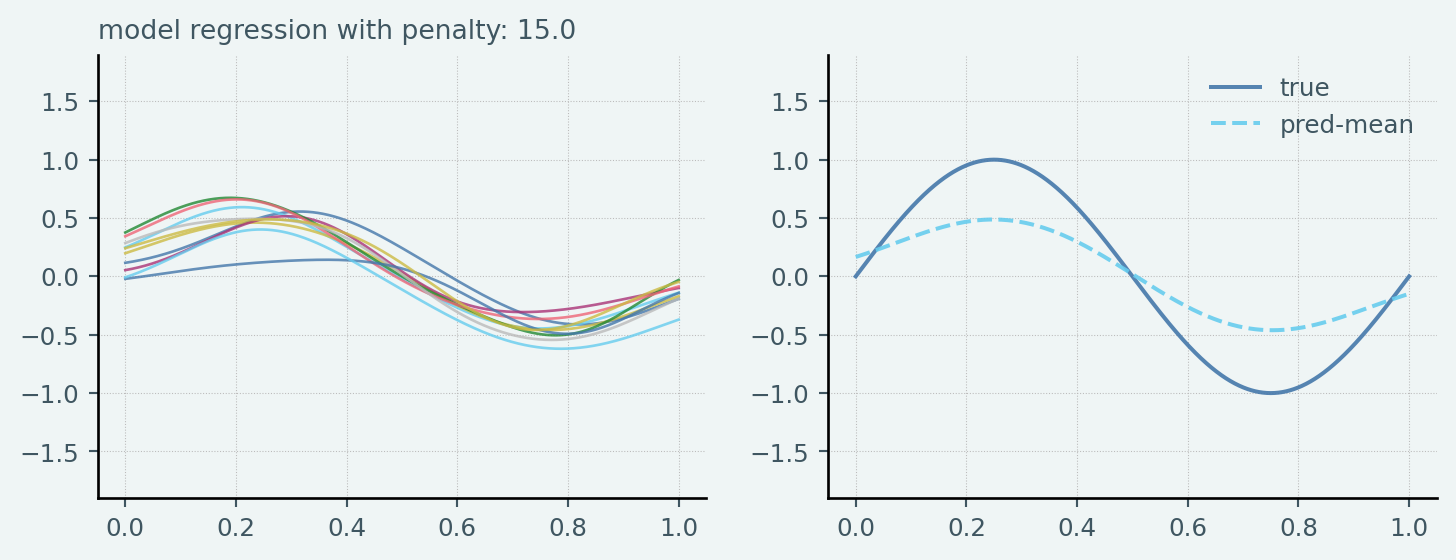
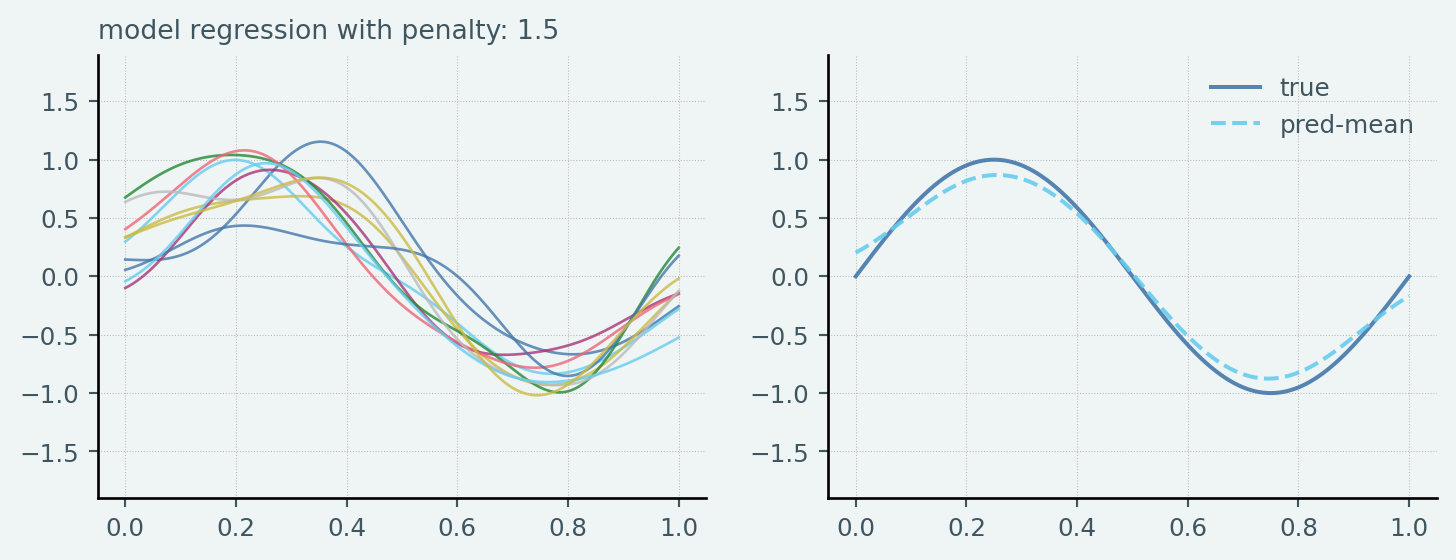
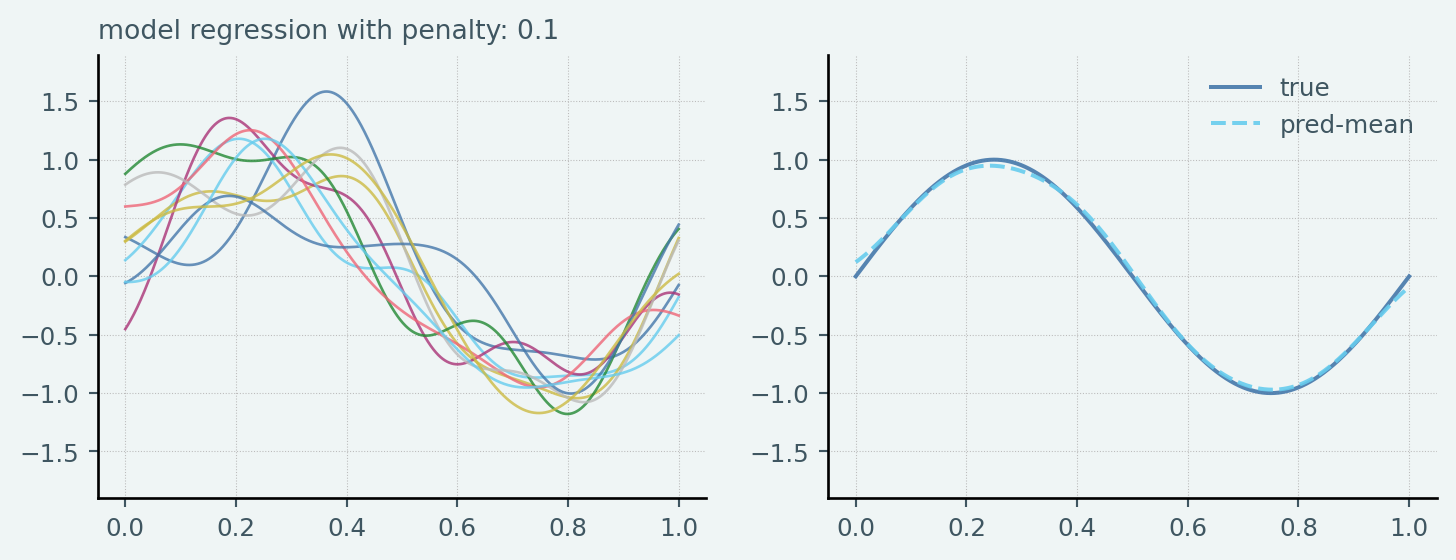
ということです．24個のガウス基底を基底関数と用いたRidge Linear Regressionをそれぞれのsampleに対して実行し，その結果得られた各予測モデル(100個の予測モデル)の予測結果についてPythonで確認してみました．

なお，Ridge penaltyは \([0.1, 1.5, 15]\) と恣意的に設定しています．なおTest datasetのsample sizeは \(N_{test} = 1000\) としています

import numpy as np
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt

import regmonkey_style.stylewizard as sw

sw.set_templates("regmonkey_line")


## create data function
def true_func(x):
    return np.sin(2 * np.pi * x)


def generate_data(func, sample_size, std, domain=[0, 1]):
    x = np.random.uniform(domain[0], domain[1], sample_size)
    t = func(x) + np.random.normal(scale=std, size=x.shape)
    return x, t


def create_gauss_basis(x, gauss_mean, gauss_var):
    if x.ndim == 1:
        x = x[:, None]
    else:
        assert x.ndim == 2
    basis = [np.ones(len(x))]
    for m in gauss_mean:
        gauss_transfomred = np.exp(-0.5 * np.square(x - m) / gauss_var)
        basis.append(gauss_transfomred.flatten())
    return np.asarray(basis).transpose()


## Generate Data
np.random.seed(1212)
gauss_basis_mean = np.linspace(0, np.pi / 2, 24)
gauss_basis_var = 0.01
penalty_list = [15, 1.5, 0.1]

x_test = np.linspace(0, 1, 1000)
X_model_test = create_gauss_basis(x_test, gauss_basis_mean, gauss_basis_var)
y_test = true_func(x_test)

x_train, y_train = generate_data(true_func, 25 * 100, 0.5)
x_train, y_train = x_train.reshape(100, 25), y_train.reshape(100, 25)


for penalty in penalty_list:
    y_list = []
    fig, axes = plt.subplots(1, 2, figsize=(9, 3))
    for i in range(100):
        X_model_train = create_gauss_basis(
            x_train[i, :], gauss_basis_mean, gauss_basis_var
        )
        clf = Ridge(alpha=penalty)
        clf.fit(X_model_train, y_train[i, :])
        y_pred = clf.predict(X_model_test)
        y_list.append(y_pred)

    for y in y_list[:10]:
        axes[0].plot(x_test, y, alpha=0.8, linewidth=1, label=f"penalty: {penalty:.2f}")
    axes[0].set_title(f"model regression with penalty: {penalty:.1f}", fontsize=10)
    for ax in axes:
        ax.set_ylim(-1.9, 1.9)
    axes[1].plot(x_test, y_test, label="true")
    axes[1].plot(
        x_test, np.asarray(y_list).mean(axis=0), linestyle="--", label="pred-mean"
    )
    axes[1].legend()
plt.show()

Bias-Variance Decompositionをシミュレーション標本で計算する場合は Equation 30.1 をシミュレーション標本と対応させれば良いので

\[ \begin{align*} \overline{f}(x) &= \frac{1}{L}\sum_l^L\hat f^{(l)}(x)\\ \operatorname{Bias}^2 &= \frac{1}{N_{test}}\sum_{n} \{\overline{f}(x_n) - h(x_n)\}^2\\ \operatorname{Variance} &= \frac{1}{N_{test}}\sum_{n}\frac{1}{L}\sum_l\left\{\hat f^{(l)}(x_n) - \overline{f}(x_n)\right\}^2 \end{align*} \]

この考えに基づいて ridge penalty に対するBias, Variance, MSEをそれぞれplotすると以下のようにトレードオフ関係が確認できます

"""
 * Computes the bias-variance decomposition for a given list of penalty values.
 * 
 * @param penalty_list - A list of penalty values.
 * @returns An array of bias and variance values corresponding to each penalty value.
"""
from multiprocessing import Pool

penalty_list = np.linspace(0.1, 8, 500)
bias_list = []
variance_list = []
h_test = true_func(x_test)

x_train, y_train = generate_data(true_func, 25 * 100, 0.5)
x_train, y_train = x_train.reshape(100, 25), y_train.reshape(100, 25)


def compute_bias_variance(penalty):
    y_list = []
    for i in range(100):
        X_model_train = create_gauss_basis(
            x_train[i, :], gauss_basis_mean, gauss_basis_var
        )
        clf = Ridge(alpha=penalty)
        clf.fit(X_model_train, y_train[i, :])
        y_pred = clf.predict(X_model_test)
        y_list.append(y_pred)
    y_list = np.asanyarray(y_list)
    bias_term = np.mean((h_test - np.mean(y_list, axis=0)) ** 2)
    variance_term = np.mean(np.mean((y_list - np.mean(y_list, axis=0)) ** 2, axis=0))

    return bias_term, variance_term


with Pool() as pool:
    results = pool.map(compute_bias_variance, penalty_list)

bias_list, variance_list = zip(*results)

import plotly.graph_objects as go

# Plot bias vs penalty
fig = go.Figure()
fig.add_trace(go.Scatter(x=penalty_list, y=bias_list, mode="lines", name="Bias"))
fig.add_trace(
    go.Scatter(x=penalty_list, y=variance_list, mode="lines", name="Variance")
)
fig.add_trace(
    go.Scatter(
        x=penalty_list,
        y=np.asarray(bias_list) + np.asarray(variance_list),
        mode="lines",
        name="Total",
    )
)
fig.update_layout(
    title="Bias-Variance decomposition", xaxis_title="Penalty", yaxis_title="Value"
)
fig.show()

Example 30.1 線形クラスにおけるBias and Variance

True functionを

\[ f(x) = \pmb{\theta}^Tx \]

と定義し，\(\pmb{\theta}\) は未知であるとします．Training dataset \(D\) を用いて，

\[ \hat f_D(x) = \widehat{\pmb{\theta}}_D^Tx \]

を学習したとします．このとき，未知のデータセット \(\pmb{S} = \{(x^*, y^*)\}\) において，

\[ \begin{align*} \text{Bias}(\hat f_D) &= \mathbb E[\hat f_D(x) - f(x) \vert \pmb{S}]\\ &= \mathbb E[\widehat{\pmb{\theta}}_D^Tx - \pmb{\theta}^Tx\vert \pmb{S}]\\ &= \mathbb E[\widehat{\pmb{\theta}}_D - \pmb{\theta}\vert \pmb{S}]^Tx\\ &= \text{Bias}(\widehat{\pmb{\theta}}_D)^Tx \end{align*} \]

同様に

\[ \begin{align*} &\operatorname{Var}(\hat f_D)\\ &= \mathbb E[(\hat f_D(x) - f(x))^2 \vert \pmb{S}]\\ &= \mathbb E[(\widehat{\pmb{\theta}}_D^Tx - \pmb{\theta}^Tx)^2\vert \pmb{S}]\\ &= \mathbb E[((\widehat{\pmb{\theta}}_D^T - \pmb{\theta}^T)x)^T((\widehat{\pmb{\theta}}_D^T - \pmb{\theta}^T)x)\vert \pmb{S}]\\ &= \mathbb E[x^T(\widehat{\pmb{\theta}}_D - \pmb{\theta})(\widehat{\pmb{\theta}}_D - \pmb{\theta})^Tx\vert \pmb{S}]\\ &= x^T\operatorname{Var}(\widehat{\pmb{\theta}})x \end{align*} \]

なお，最後の式変形は \(a\) を定数としたときに \(\operatorname{Var}(a - X) = \operatorname{Var}(X)\) を用いています．

🍵 Green Tea Break

予測におけるBias-Variance分解は Overfitting，Underfitting という結びつけて考えることができます．

▶  Overfitting

training dataにおける予測精度はとても良いがtest dataにおける予測精度がとても悪い予測モデルに対してOverfittingという評価をします．これは予測モデルがtraining dataのノイズを拾いすぎてしまったときに発生します．

Overfittingは表現力(capacity)の高いモデルを用いたときに発生する可能性が高いです．実際に発生したときは，

• high bias and high variance
• low bias and high variance

いずれも考えることができますが，基本的にはhigh varianceを疑いアクションをとるという対処方針となります，対処方法として，

• 正則化
• より大きいデータセットの活用
• inputeとして用いる特徴量の数を少なくする
• より表現力が狭められたモデルを学習モデルに用いる
• BoostingよりBagging

といったことをトライすることが推奨されます．

▶  Underfitting

Underfittingとは，training dataにおいても十分な学習ができていない状況を指す概念です． モデルの表現力が低い場合に起きることが多く，またhigh biasの状況と関連しているケースが多いです．この場合，traing dataset自体にfitできていないので，さらなるデータ収集することは費用対効果に見合いません．

• 罰則項の緩和
• 特徴量の拡充
• より表現力のあるモデルのトライ
• Boosting

が推奨されます．

▶  Rule of thumbs

汎化性能が悪い場合に，まずbias-varianceのどちらの要因が重きを占めているのか？を考えることが重要です．その判別方法として経験則的に知られているステップとして，

• Training data errorが大きい場合は，もしモデルがトレーニングデータ自体にうまくフィットできないということになるので，そのモデルはhigh biasを持っている可能性が高いと判断する
• Cross validation errorとprediction erro in training datasetの差は、モデルや推定量の分散として扱うことができるので，Cross validation errorが高い場合は overfitting の状態と判断する

Training dataset errorに比べCross validation errorが高いときに，線形モデルからneural networkモデルへ変更することはあまり意味のない（むしろ状況を悪化させる）となるケースが多いというアクションになります．

Decomposition of Expected Test Error

上では未知のデータセット \(\{x^*, y^*\}\) について \(\{x^*\}\) コントロールしたときのBias-Variance Decompositionを確認しましたが 未知のデータセット \((\pmb{x}, y)\) とtraining dataset \(D\) についてのexptected decompositonを確認していきます．

なお，Expected Prediction functionについて以下のnotationを導入します

\[ \bar{f} = E_{D} \left[ \hat f_D \right] = \int\limits_D \hat f_D \Pr(D) \partial D \]

\(\bar{f}\) は \(D\) の確率で重みづけたそれぞれの予測関数のweighted averageと理解できます．

\[ \begin{align*} &\mathbb E_{\pmb x, y, D}[(\hat f_D(\pmb x) - y)^2]\\ &= \mathbb E_{\pmb x, y, D}[(\hat f_D(\pmb x) - \bar{f}(\pmb x) + \bar{f}(\pmb x) - y)^2]\\ &= \underbrace{\mathbb E_{\pmb x, D}[(\hat f_D(\pmb x) - \bar{f}(\pmb x))^2]}_{\text{Variance}} + \mathbb E_{\pmb x, y}[(\bar{f}(\pmb x) - y)^2] \end{align*} \tag{30.2}\]

なお途中の式変形において次の性質を利用しています

\[ \begin{align*} &\mathbb E_{\mathbf{x}, y, D} \left[\left(\hat f_{D}(\mathbf{x}) - \bar{f}(\mathbf{x})\right) \left(\bar{f}(\mathbf{x}) - y\right)\right] \\ &= \mathbb E_{\mathbf{x}, y} \left[E_{D} \left[ \hat f_{D}(\mathbf{x}) - \bar{f}(\mathbf{x})\right] \left(\bar{f}(\mathbf{x}) - y\right) \right] \because{\text{LIE}}\\ &= \mathbb E_{\mathbf{x}, y} \left[ \left( E_{D} \left[ \hat f_{D}(\mathbf{x}) \right] - \bar{f}(\mathbf{x}) \right) \left(\bar{f}(\mathbf{x}) - y \right)\right] \\ &= \mathbb E_{\mathbf{x}, y} \left[ \left(\bar{f}(\mathbf{x}) - \bar{f}(\mathbf{x}) \right) \left(\bar{f}(\mathbf{x}) - y \right)\right] \\ &= \mathbb E_{\mathbf{x}, y} \left[ 0 \right] \\ &= 0 \end{align*} \]

次に，Equation 30.2 の第二項について考えます．

\[ \begin{align*} &\mathbb E_{\pmb x, y}[(\bar{f}(\pmb x) - y)^2]\\ &= \mathbb E_{\pmb x, y}[(\bar{f}(\pmb x) - h(\pmb x) + h(\pmb x) - y)^2]\\ &= \mathbb E_{\pmb x}[(\bar{f}(\pmb x) - h(\pmb x))^2] + \mathbb E_{\pmb x, y}[(h(\pmb x) - y)^2]\\ &= \mathbb E_{\pmb x}[\text{Bias}^2(\pmb{x})] + \mathbb E_{\pmb x}[\mathbb E[\epsilon^2 \vert \pmb{x}]]\\ &= \mathbb E[\text{Bias}^2] + \mathbb E[\epsilon^2] \end{align*} \]

以上より

\[ \mathbb E_{\pmb x, y, D}[(\hat f_D(\pmb x) - y)^2] = \mathbb E[\text{Variance of }\hat f_D] + \mathbb E[\text{Bias}^2] + \mathbb E[\epsilon^2] \]