複素数の性質
Def: 複素数
2つの実数 \(a, b\) を用いて
\[
z = a + bi
\]
と表される数 \(z\) を複素数という.\(a\) を上の複素数の実部,\(b\) を虚部と呼ぶ. 複素数全体の集合は一般に \(\mathbb C\) と表される.
複素数 \(z = a + bi\) の実数の組 \((a, b)\) について,
\[
\begin{align*}
a &= \text{Re}\, z\\
b &= \text{Im}\, z
\end{align*}
\]
と表したりします.それぞれ,real part, imaginary partの略と理解できます.
▶ 複素数の加減乗除
\(z_1 = a + bi, z_2 = c + di\) としたとき,四則演算は以下のように計算されます
\[
\begin{align*}
z_1 + z_2 &= (a + c) + (b + d)i\\
z_1 - z_2 &= (a - c) + (b - d)i\\
z_1z_2 &= ac + (ad + bc)i + bdi^2\\
&= (ac - bd) + (ad + bc)i \quad \because i^2 =-1\\
\frac{z_1}{z_2}
&= \frac{a + bi}{c + di}\\
&= \frac{a + bi}{c + di}\frac{c - di}{c - di}\\
&= \frac{(a + bi)(c - di)}{c^2+d^2}\\
&= \frac{(ac + bd) + (bc - ad)i}{c^2+d^2}
\end{align*}
\]
Def: 共役複素数
複素数 \(z = a+bi\) に対し,
\[
\bar z = a - bi
\]
を \(z\) の共役複素数(きょうやくふくそすう)と呼ぶ.
共役複素数は,複素数平面上で実軸に関して対称移動させたものと解釈することができます.また,定義より自明ですが 複素数と共役複素数について,和と積が実数になるという特徴もあります.
Theorem C.1
2つの複素数 \(z_1, z_2\) について,次が成り立つ
\[
\begin{align*}
\overline{z_1 + z_2} &= \bar z_1 + \bar z_2\\
\overline{z_1z_2} &= \bar z_1\bar z_2
\end{align*}
\]
\(z_1 = a_1 + b_1i, z_2 = a_2 + b_2i\) としたとき,
\[
\begin{align*}
\overline{z_1 + z_2}
&= \overline{(a_1 + a_2) + (b_1 +b_2)i}\\
&= (a_1 + a_2) - (b_1 +b_2)i\\
&= a_1 - b_1i + a_2 - b_2i\\
&= \bar z_1 + \bar z_2
\end{align*}
\]
積については
\[
\begin{align*}
\overline{z_1z_2}
&= \overline{(a_1a_2 - b_1b_2) + (a_1b_2 + a_2b_1)i}\\
&= (a_1a_2 - b_1b_2) - (a_1b_2 + a_2b_1)i\\
&= a_1a_2 - (a_1b_2 + a_2b_1)i + b_1b_2i^2\\
&= (a_1 - b_1i)(a_2 - b_2i)\\
&= \bar z_1\bar z_2
\end{align*}
\]
Def: 複素数の絶対値
複素数 \(z = a + bi\) の絶対値 \(\vert z\vert\) は次のように計算される:
\[
\vert z \vert = \sqrt{a^2 + b^2}
\]
定義より,\((a, b) = (0, 0)\) のときは,\(\vert z\vert =0\).逆に \(\vert z\vert =0\) ならば,
\[
a^2 + b^2 =0
\]
を満たす実数の組は \((0, 0)\) しか存在しないので,\(z = 0\) となります.
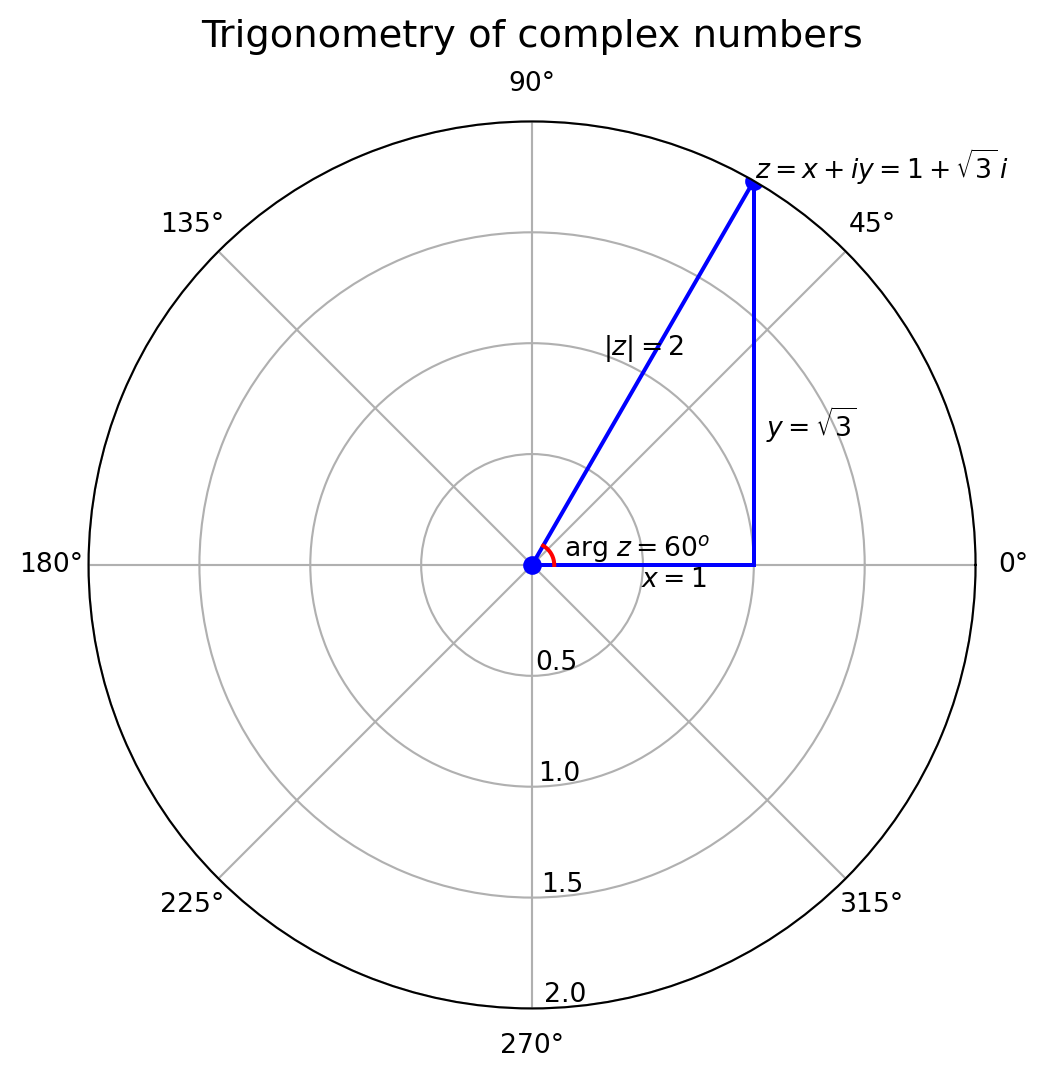
複素平面
複素数 \(z = x + yi\) が与えられたとき,2つの実数の組 \((x, y)\) が与えられた状況とも解釈できます. また,2つの実数の組 \((x, y)\) が与えられた状況とは,\(xy\)-平面上の点を与えられる状況とも考えることができます. つまり,複素数が与えられたとき,
とする \(xy\)-平面を考えることができます.\(z = 1 + \sqrt{3}\) を描いてみると,
Code
import matplotlib.pyplot as plt
import numpy as np
pi = np.pi
# Set parameters
r = 2
theta = pi/3
x = r * np.cos(theta)
x_range = np.linspace(0, x, 1000)
theta_range = np.linspace(0, theta, 1000)
# Plot
fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111, projection='polar')
ax.plot((0, theta), (0, r), marker='o', color='b') # Plot r
ax.plot(np.zeros(x_range.shape), x_range, color='b') # Plot x
ax.plot(theta_range, x / np.cos(theta_range), color='b') # Plot y
ax.plot(theta_range, np.full(theta_range.shape, 0.1), color='r') # Plot theta
ax.margins(0) # Let the plot starts at origin
ax.set_title("Trigonometry of complex numbers", va='bottom',
fontsize='x-large')
ax.set_rmax(2)
ax.set_rticks((0.5, 1, 1.5, 2)) # Less radial ticks
ax.set_rlabel_position(-88.5) # Get radial labels away from plotted line
ax.text(theta, r+0.01 , r'$z = x + iy = 1 + \sqrt{3}\, i$') # Label z
ax.text(theta+0.2, 1 , r'$\vert z\vert = 2$') # Label r
ax.text(0-0.2, 0.5, '$x = 1$') # Label x
ax.text(0.5, 1.2, r'$y = \sqrt{3}$') # Label y
ax.text(0.25, 0.15, r'$\text{arg } z = 60^o$') # Label theta
ax.grid(True)
plt.show()
複素数が \(xy\)-平面上の点で表すことができるということは,原点からの長さと角度 \((r, \theta)\) によって点を表現できることになります. このとき,以下のように表します:
\[
\begin{align*}
r & = \vert z\vert\\
\theta &= \operatorname{arg}z = \arctan \left(\frac{y}{x}\right)
\end{align*}
\]
このことから次の定義が導けます.
Def: 複素数の極形式
複素平面上の点 \(z = x + yi\) は極座標を用いて次のように表せる:
\[
\begin{align*}
&z = r(\cos \theta + i\sin\theta)\\
&\text{where } r = \vert z\vert, \theta = \operatorname{arg} z
\end{align*}
\]
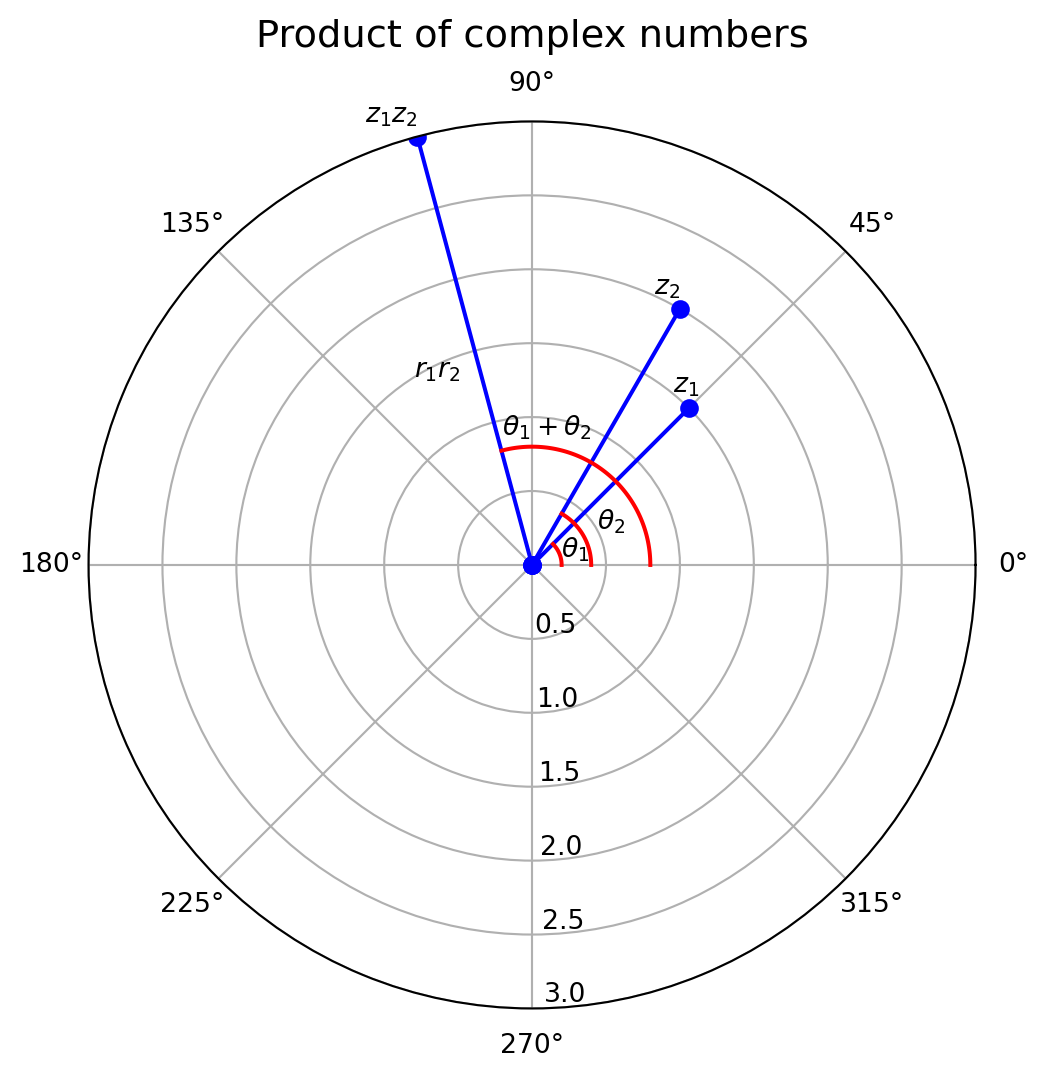
▶ 複素数の積と複素平面
2つの複素数 \(z_1 = r_1(\cos\theta_1 + i\sin\theta_1), z_2 = r_2(\cos\theta_2 + i\sin\theta_2)\) に対して,その積は
\[
\begin{align*}
z_1z_2
=& r_1r_2(\cos\theta_1 + i\sin\theta_1)(\cos\theta_2 + i\sin\theta_2)\\
=& r_1r_2\{(\cos\theta_1\cos\theta_2 - \sin\theta_1\sin\theta_2) \\
& + i(\sin\theta_1\cos\theta_2 + \cos\theta_1\sin\theta_2)\}\\
=& r_1r_2\{\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)\} \because{\text{加法定理}}
\end{align*}
\]
\(xy\)-平面で確認すると以下のようになります
Code
import matplotlib.pyplot as plt
import numpy as np
pi = np.pi
# Set parameters
r_1 = 1.5
r_2 = 2
theta_1 = pi / 4
theta_2 = pi / 3
x_1 = r_1 * np.cos(theta_1)
x_2 = r_2 * np.cos(theta_2)
theta_range = np.linspace(0, theta, 1000)
# Plot
fig = plt.figure(figsize=(6, 6))
ax = plt.subplot(111, projection="polar")
ax.plot((0, theta_1), (0, r_1), marker="o", color="b")
ax.plot((0, theta_2), (0, r_2), marker="o", color="b")
ax.plot((0, theta_1 + theta_2), (0, r_1 * r_2), marker="o", color="b")
ax.margins(0) # Let the plot starts at origin
ax.set_title("Product of complex numbers", va="bottom", fontsize="x-large")
ax.set_rmax(3)
ax.set_rticks((0.5, 1, 1.5, 2, 2.5, 3)) # Less radial ticks
ax.set_rlabel_position(-88.5) # Get radial labels away from plotted line
ax.text(theta_1 + 0.1, r_1 + 0.01, r"$z_1$")
ax.text(theta_2 + 0.1, r_2 + 0.01, r"$z_2$")
ax.text(theta_1 + theta_2 + 0.1, r_1 * r_2 + 0.2, r"$z_1z_2$")
ax.text(theta_1 + theta_2 + 0.3, (r_1 * r_2) / 2, r"$r_1r_2$")
theta1_range = np.linspace(0, theta_1, 100)
theta2_range = np.linspace(0, theta_2, 100)
theta3_range = np.linspace(0, theta_1 + theta_2, 100)
ax.plot(theta1_range, np.full(theta1_range.shape, 0.2), color="r") # Plot theta
ax.plot(theta2_range, np.full(theta2_range.shape, 0.4), color="r") # Plot theta
ax.plot(theta3_range, np.full(theta3_range.shape, 0.8), color="r") # Plot theta
ax.text(0.25, 0.2, r"$\theta_1$") # Label theta
ax.text(0.5, 0.5, r"$\theta_2$") # Label theta
ax.text(1.8, 0.9, r"$\theta_1 + \theta_2$") # Label theta
ax.grid(True)
plt.show()
📘 REMARKS
2つの複素数 \(z_1, z_2\) に対して,
\[
\begin{align*}
\vert z_1z_2\vert &= \vert z_1\vert \cdot \vert z_2\vert\\
\operatorname{arg}(z_1z_2) &= \operatorname{arg} z_1 + \operatorname{arg} z_2
\end{align*}
\]
2つ以上の複素数の積についても,繰り返すことによって以下の関係性を得ます.
\[
\prod_i^nz_i = r_1r_2\cdots r_n\left\{\cos\left(\sum_i\theta_i\right) + i\sin\left(\sum_i\theta_i\right)\right\}
\]
これはド・モアブルの公式と呼ばれているものです.
Theorem C.2 : ド・モアブルの公式
\(n\in\mathbb Z\) としたとき
\[
(\cos\theta + i\sin\theta)^n = \cos n\theta + i\sin n\theta
\]
\(n \geq 0\) は自明なので,ここでは \(n < 0\) の場合を示す.
\[
(\cos\theta + i\sin\theta)^n = \frac{1}{(\cos\theta + i\sin\theta)^{-n}}
\]
\(-n > 0\) より
\[
\begin{align*}
\frac{1}{(\cos\theta + i\sin\theta)^{-n}}
&= \frac{1}{\cos (-n\theta) + i\sin (-n\theta)}\\
&= \frac{1}{\cos (-n\theta) + i\sin (-n\theta)}\frac{\cos (-n\theta) - i\sin (-n\theta)}{\cos (-n\theta) - i\sin (-n\theta)}\\
&= \cos (-n\theta) - i\sin (-n\theta)\\
&= \cos (n\theta) + i\sin (n\theta)
\end{align*}
\]
従って,\(n\in \mathbb Z\) でド・モアブルの公式が成立することが分かる.
オイラーの公式
Def: オイラーの公式
\[
\begin{align*}
\exp(i\theta) &= \cos\theta + i\sin\theta\\
\exp(-i\theta) &= \cos\theta - i\sin\theta
\end{align*}
\]
\(\cos x, \sin x, \exp(ix)\) をマクローリン展開します.
\[
\begin{align*}
\sin(x) =& x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - \cdots + (-1)^n\frac{1}{(2n+1)!}x^{2n+1} + \cdots\\
\cos(x) =& 1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 - \cdots + (-1)^n\frac{1}{(2n)!}x^{2n} + \cdots\\
\exp(ix)=& 1 + ix - \frac{1}{2!}x^2 + i\frac{1}{3!}x^3 + \cdots + i^n\frac{1}{n!}x^n + \cdots\\
=& \left(1 - \frac{1}{2!}x^2 + \frac{1}{4!}x^4 + \cdots \right)\\
&+ \left( - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - \cdots \right)
\end{align*}
\]
実部・虚部を比較すると,
\[
\exp(i\theta) = \cos\theta + i\sin\theta
\]
を得ます.また,\(\cos\theta = \cos(-\theta), \sin\theta = -\sin(-\theta)\) より,
\[
\exp(-i\theta) = \cos\theta - i\sin\theta
\]
▶ オイラーの公式と加法定理
オイラーの公式より加法定理を確認することができます.
\[
\begin{align*}
\cos(\alpha+\beta) + i\sin(\alpha+\beta)
=& \exp(i(\alpha+\beta))\\
=& \exp(i\alpha)\exp(i\beta)\\
=& (\cos\alpha\cos\beta - \sin\alpha\sin\beta)\\
&+ i(\cos\alpha\sin\beta + \sin\alpha\cos\beta)
\end{align*}
\]
実部と虚部を比較すると
\[
\begin{align*}
\cos(\alpha+\beta) &= \cos\alpha\cos\beta - \sin\alpha\sin\beta\\
\sin(\alpha+\beta) &= \sin\alpha\cos\beta + \cos\alpha\sin\beta
\end{align*}
\]
同様に
\[
\begin{align*}
\cos(\alpha-\beta) + i\sin(\alpha-\beta)
=& \exp(i(\alpha-\beta))\\
=& \exp(i\alpha)\exp(-i\beta)\\
=& (\cos\alpha\cos\beta + \sin\alpha\sin\beta)\\
&+ i(\sin\alpha\cos\beta - \cos\alpha\sin\beta )
\end{align*}
\]
従って,
\[
\begin{align*}
\cos(\alpha-\beta) &= \cos\alpha\cos\beta + \sin\alpha\sin\beta\\
\sin(\alpha-\beta) &= \sin\alpha\cos\beta - \cos\alpha\sin\beta
\end{align*}
\]
▶ 三角関数の微分との関係
\(\theta\) について,\(\exp(i\theta)\) を微分すると
\[
\begin{align*}
(\exp(i\theta))^\prime
&= i\exp(i\theta)\\
&= i(\cos\theta + i\sin\theta)\\
&= -\sin\theta + i\cos\theta
\end{align*}
\]
同様に
\[
\begin{align*}
(\cos\theta + i\sin\theta)^\prime
&= \frac{\,\mathrm{d}}{\,\mathrm{d}\theta}\cos\theta + \frac{\,\mathrm{d}}{\,\mathrm{d}\theta}i\sin\theta
\end{align*}
\]
実部と虚部を比較することで,三角関数の微分の公式を得ることができます.
▶ 三角関数の表現
オイラーの公式より,三角関数を次のように表せます.
\[
\begin{align*}
\cos\theta &= \frac{\exp(i\theta)+\exp(-i\theta)}{2}\\
\sin\theta &= \frac{\exp(i\theta)-\exp(-i\theta)}{2i}
\end{align*}
\]
これを用いると以下の積分が簡単に計算できます.
\[
\begin{split}
\begin{aligned}
\int \cos(\theta) \sin(\theta) \, \mathrm{d}\theta
&=
\int
\frac{(e^{i\theta} + e^{-i\theta})}{2}
\frac{(e^{i\theta} - e^{-i\theta})}{2i}
\, \mathrm{d}\theta \\
&=
\frac{1}{4i}
\int
e^{2i\theta} - e^{-2i\theta}
\, d\theta \\
&=
\frac{1}{4i}
\bigg( \frac{-i}{2} e^{2i\theta} - \frac{i}{2} e^{-2i\theta} + C_1 \bigg) \\
&=
-\frac{1}{8}
\bigg[ \bigg(e^{i\theta}\bigg)^2 + \bigg(e^{-i\theta}\bigg)^2 - 2 \bigg] + C_2 \\
&=
-\frac{1}{8} (e^{i\theta} - e^{-i\theta})^2 + C_2 \\
&=
\frac{1}{2} \bigg( \frac{e^{i\theta} - e^{-i\theta}}{2i} \bigg)^2 + C_2 \\
&= \frac{1}{2} \sin^2(\theta) + C_2
\end{aligned}
\end{split}
\]
従って,
\[
\int^{2\pi}_0 \cos(\theta) \sin(\theta) \, \mathrm{d}\theta = 0
\]