カイ2乗分布の性質
\(i \in \{1, \cdots, n\}\) について \(Z_i \overset{\mathrm{iid}}{\sim} N(0, 1)\) のとき,
\[
X = \sum_i Z_i^2
\]
とすると,自由度 \(n\) の中心カイ2乗分布に従うとされます,\(X \sim \operatorname{\chi^2}(n)\). 母分散の区間推定や適合度や独立性の検定の際に使用されたりします.
Def: 中心カイ2乗分布
連続確率変数 \(X\) が自由度 \(n\) の中心カイ2乗分布に従うとき,その確率密度関数 \(f(x)\) は
\[
f(x) = \frac{1}{2^{n/2}\Gamma(n/2)}x^{n/2-1}\exp(-x/2), \quad (x > 0)
\]
Code
from scipy import stats
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from regmonkey_style import stylewizard as sw
sw.set_templates("regmonkey_line")
fig, axes = plt.subplots(1, 2, figsize=(8.8, 6))
dof = [1, 2, 3, 4, 6]
x_grid = np.linspace(0, 15, 100)
for _n in dof:
z = stats.chi2(df=_n)
axes[0].plot(x_grid, z.pdf(x_grid), alpha=0.8, lw=2, label=f"dof={_n}")
axes[1].plot(x_grid, z.cdf(x_grid), alpha=0.8, lw=2, label=f"dof={_n}")
axes[0].set_ylabel("PDF")
axes[1].set_ylabel("CDF")
for ax in axes:
ax.set_ylim(0, 1.05)
ax.set_xlim(0, 12)
ax.set_xlabel("x")
axes[0].set_title("PDF of chi-squared distribution", fontsize=14)
axes[1].set_title("CDF of chi-squared distribution", fontsize=14)
axes[1].legend()
plt.show()
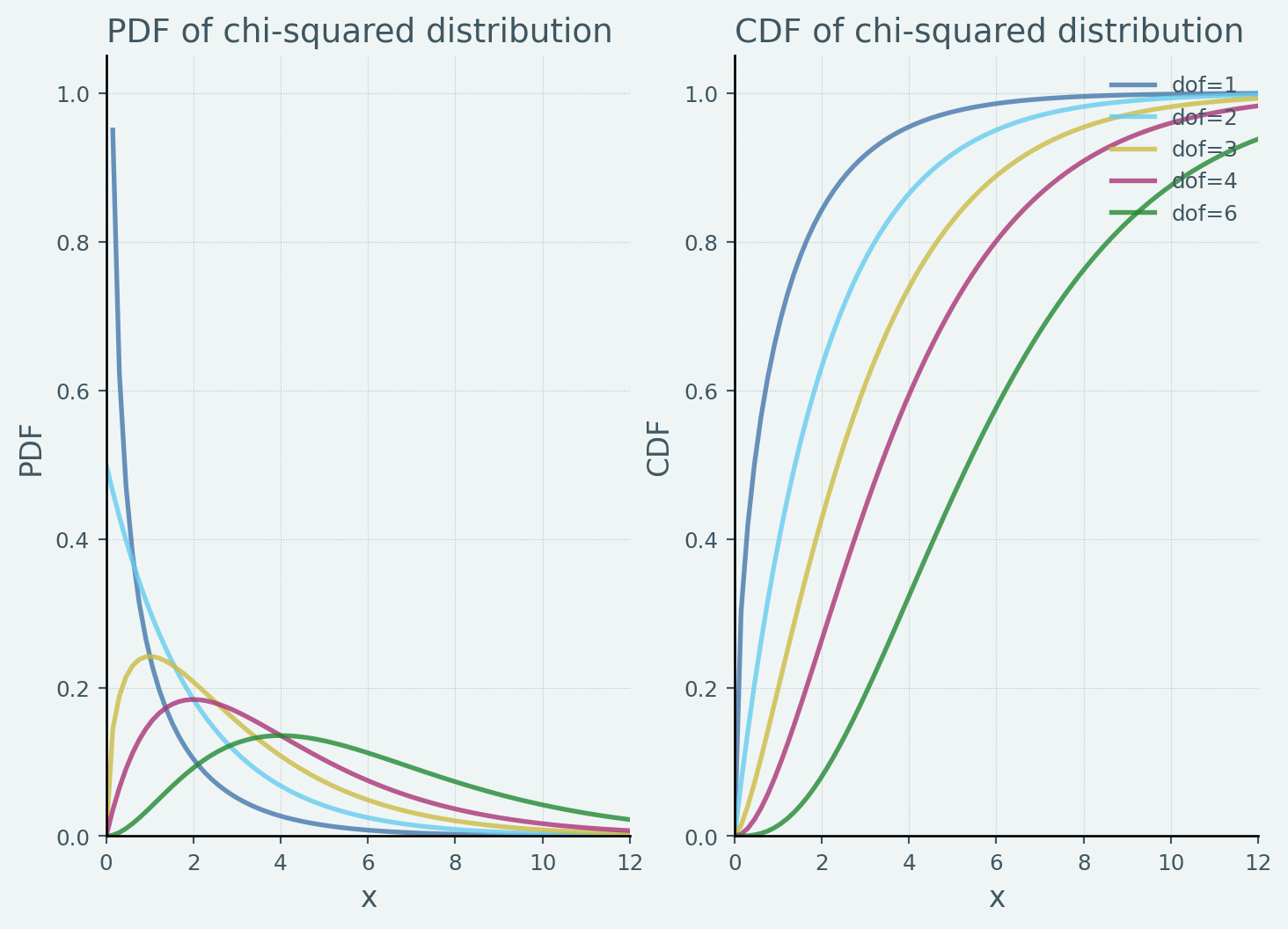
確率密度関数に着目すると自由度 \(n > 2\) について最頻値は,\(x = n-2\) の点となることがわかります.
▶ 期待値の導出
\(X \sim \operatorname{\chi^2}(n)\) の期待値は
\[
\begin{align*}
\mathbb E[X]
&= \int^\infty_0 x \frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}\exp(-x/2)\,\mathrm{d}x\\
&= 2\frac{n}{2}\int^\infty_0\frac{1}{2^{\frac{n}{2}+1}\Gamma(\frac{n}{2}+1)}x^{(\frac{n}{2}+1)-1}\exp(-x/2)\,\mathrm{d}x\\
&= n
\end{align*}
\]
または,標準正規分布に独立に従う\(n\) 個の確率変数の二乗和として計算することもできます.
\[
\begin{align*}
Z&\overset{\mathrm{iid}}{\sim} N(0, 1)\\
\mathbb E[X]
&= \mathbb E[Z_1^2 + \cdots + Z_n^2]\\
&= \mathbb E[Z_1^2] + \cdots + \mathbb E[Z_n^2]\\
&= \operatorname{Var}(Z_1) + \cdots + \operatorname{Var}(Z_n)\\
&= n
\end{align*}
\]
▶ 分散の導出
\(X \sim \operatorname{\chi^2}(n)\) について
\[
\begin{align*}
\mathbb E[X^2]
&= \int^\infty_0 x^2 \frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}\exp(-x/2)\,\mathrm{d}x\\
&= 2^2\frac{n}{2}\frac{n+2}{2}\int^\infty_0\frac{1}{2^{\frac{n}{2}+2}\Gamma(\frac{n}{2}+2)}x^{(\frac{n}{2}+2)-1}\exp(-x/2)\,\mathrm{d}x\\
&= n(n+2)
\end{align*}
\]
従って,
\[
\begin{align*}
\operatorname{Var}(X)
&= \mathbb E[X^2] - \mathbb E[X]^2\\
&= n(n+2) - n^2\\
&= 2n
\end{align*}
\]
または,標準正規分布に独立に従う\(n\) 個の確率変数の二乗和の性質を利用して計算することもできます. 標準正規分布の尖度は \(3\) であるので,
\[
\begin{align*}
\operatorname{Var}(X)
&=\operatorname{Var}(Z_1^2 + \cdots + Z_n^2)\\
&=\operatorname{Var}(Z_1^2) + \cdots + \operatorname{Var}(Z_n^2)\\
&= n (\mathbb E[Z_i^4] - \mathbb E[Z_i^2]^2)\\
&= n(3-1)\\
&=2n
\end{align*}
\]
▶ MGFの導出
\(X \sim \operatorname{\chi^2}(n)\) について
\[
\begin{align*}
M_X(t)
&= \int^\infty_0 \exp(tx) \frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}\exp(-x/2)\,\mathrm{d}x\\
&= \int^\infty_0\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}\exp(-x(1-2t)/2)\,\mathrm{d}x
\end{align*}
\]
ここで \(x = \frac{1}{1-2t}z\) と変数変換すると
\[
\begin{align*}
&\int^\infty_0\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}x^{\frac{n}{2}-1}\exp(-x(1-2t)/2)\,\mathrm{d}x \\
&= [1 - 2t]^{-\frac{n}{2}-1}(1 - 2t)\int^\infty_0\frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}z^{\frac{n}{2}-1}\exp(-z/2)\,\mathrm{d}z\\
&= [1 - 2t]^{-\frac{n}{2}}
\end{align*}
\]
なお,\(x > 0\) より
\[
\begin{align*}
\frac{1}{1-2t}z > 0 \Rightarrow t < \frac{1}{2}
\end{align*}
\]
▶ 特性関数の導出
カイ2乗分布の再生性
Theorem 19.1
確率変数 \(X_1, \cdots, X_k\) について \(X_i \overset{\mathrm{iid}}{\sim} \operatorname{\chi^2}(n_i)\) とする.このとき, \(Y = \textstyle\sum_{i=1}^k X_i\) と変数を定義すると
\[
Y \sim \operatorname{\chi^2}(\textstyle\sum_{i=1}^k n_i)
\]
MGFを用いると
\[
\begin{align*}
M_Y(t)
&= \textstyle\prod M_{X_i}(t)\\[5pt]
&= \textstyle\prod [1 - 2t]^{-n_i/2}\\[5pt]
&= \textstyle\prod [1 - 2t]^{-\sum n_i/2}
\end{align*}
\]
これは \(\operatorname{\chi^2}(\textstyle\sum_{i=1}^k n_i)\) のMGFと一致する.
他の確率分布との関係
Theorem 19.2 : 標準正規分布と中心カイ2乗分布
確率変数 \(Z\sim N(0, 1)\) について,\(U = Z^2\) としたとき
\[
U \sim \operatorname{\chi^2}(1)
\]
\(U = Z^2\) は平方変換なので PDFは \(u \geq 0\) について
\[
\begin{align*}
f_U(u)
&= \frac{\,\mathrm{d}}{\,\mathrm{d}u} P(Z \in \{z\vert -\sqrt{u} \leq z \sqrt{u} \})\\
&= \frac{\,\mathrm{d}}{\,\mathrm{d}u} \int^{\sqrt{u}}_{-\sqrt{u}} \frac{1}{2\pi}\exp\left(-\frac{z^2}{2}\right)\,\mathrm{d}z\\
&= \frac{1}{2}\frac{1}{\sqrt{u}}\left[\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{u}{2}\right) + \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{u}{2}\right)\right]\\
&= \frac{1}{\sqrt{2\pi}}u^{-\frac{1}{2}}\exp\left(-\frac{u}{2}\right)\\
&= \frac{1}{2^{1/2}\Gamma(1/2)}u^{-\frac{1}{2}}\exp\left(-\frac{u}{2}\right)
\end{align*}
\]
\(u < 0\) については \(f_u(u) = 0\) であるので,\(U\) のPDFは \(\operatorname{\chi^2}(1)\) のPDFと一致することが示せました.
Theorem 19.3
確率変数 \(Z_i \overset{\mathrm{iid}}{\sim} N(0, 1), i = 1, 2, 3, \cdots, n\) について,
\[
Y = \textstyle\sum_{i=1}^n Z_i^2
\]
としたとき,\(Y \sim \operatorname{\chi^2}(n)\)
\(Z_i^2 \sim \operatorname{\chi^2}(1)\) であるので,
\[
M_{Z_i}(t) = [1 - 2t]^{-\frac{1}{2}}
\]
\(\{Z_i\}_{i=1}^n\) は仮定より互いに独立なので,
\[
\begin{align*}
M_Y(t)
&= \prod_{i=1}^n M_{Z_i}(t)\\
&= \prod_{i=1}^n [1 - 2t]^{-\frac{1}{2}}\\
&= [1 - 2t]^{-\frac{n}{2}}
\end{align*}
\]
これは \(\operatorname{\chi^2}(n)\) のMGFと一致するので \(Y \sim \operatorname{\chi^2}(n)\)
Theorem 19.4 正規分布に従う確率変数の不偏分散
確率変数 \(X_i \overset{\mathrm{iid}}{\sim} N(\mu, \sigma^2), i = 1, \cdots, n\) について
\[
\begin{align*}
\overline{X} &= \frac{1}{n}\sum X_i\\
S^2 &= \frac{1}{n} \sum (X_i - \overline{X})^2
\end{align*}
\]
としたとき,
\[
(n-1)\frac{S^2}{\sigma^2} \sim \operatorname{\chi^2}(n-1)
\]
▶ Assumption
\[
\begin{align*}
\overline{X} &= \frac{1}{n}\sum X_i\\
S^2 &= \frac{1}{n} \sum (X_i - \overline{X})^2\\
\Rightarrow &\overline{X} \perp S^2
\end{align*}
\]
▶ Proof
\[
\begin{align*}
\sum \left(\frac{X_i - \mu}{\sigma}\right)^2
&= \frac{1}{\sigma}\sum \left(X_i - \overline{X} + \overline{X} - \mu\right)^2\\
&= \frac{1}{\sigma}\sum (X_i - \overline{X})^2 + \left(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\right)^2\\
&= \frac{n-1}{\sigma}S^2 + \left(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\right)^2
\end{align*}
\]
このとき,
\[
\begin{gather}
\sum \left(\frac{X_i - \mu}{\sigma}\right)^2 \sim \operatorname{\chi^2}(n)\\
\left(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\right)^2 \sim \operatorname{\chi^2}(1)\\[5pt]
\overline{X} \perp S^2
\end{gather}
\]
であるので,
\[
\frac{n-1}{\sigma}S^2 \sim \operatorname{\chi^2}(n-1)
\]