26  M-Estimator

M-estimatorの「M」はmaximum-likelihood-typeを意味しており，M-estimatorはMLEを一般化した推定量です．

M-Estimator

Def: M-estimator

\((x_i, y_i)\) を母集団からのサイズ \(n\) のi.i.d ランダムサンプリングとする．このとき，

\[ \begin{align*} &\hat\beta = \arg\min_{\beta} \sum_{i=1}^n \rho(x_i, y_i;\beta)\\ &\text{where } \rho \text{ is some suitably chosen function} \end{align*} \] として推定量を考えるとき，これをM-estimatorと呼ぶ．

\(\rho(\cdot)\) はロス関数(一般的には非負の関数)とも呼ばれたりします．この形状を操作することで，M-estimatorは

• MLE
• ロバスト推定量
• ベイズ事前分布に基づく推定量

に対応させることができます．

\[ \begin{gather} \frac{\mathrm{d}}{\mathrm{d \theta}} \rho(x_i;\theta) = 0\\ \sum_i \varphi(x_i;\theta) = 0 \text{という形で表されることが多い} \end{gather} \]

から導出される方程式を核関数(以下, \(\varphi(\cdot)\) で表記)とよんだりします．

▶  標本平均とMedianとM-estimator

標本平均 \(\overline{X}\) もM-estimatorの枠組みで理解でき，

\[ \begin{align*} \rho(x-\mu) &= (x-\mu)^2\\ \varphi(x-\mu) &= (x-\mu) \end{align*} \]

に対応します．また，メディアンは

\[ \begin{align*} \rho(x-a) &= \vert x-a\vert \\ \varphi(x-a) &= -\mathbb 1(x < a) + \mathbb 1(x > a) \end{align*} \]

に対応します．

Example 26.1 : 正規分布パラメーターについてのMLE

確率変数 \(x_i\sim N(\mu, \sigma^2)\) について，\(\theta = (\mu, \sigma^2)\) を推定したいとします．このとき，

\[ \begin{align*} \hat\theta &= \arg\max \sum_{i=1}^n\log(\phi(x_i; \theta))\\ &= \arg\max \sum_{i=1}^n \left(-\frac{(x_i-\mu)^2}{2\sigma^2} - \frac{1}{2}\log\sigma^2- \frac{1}{2}\log(2\pi)\right) \end{align*} \]

\(\mu, \sigma^2\) についてFOCを整理すると，

\[ \begin{align*} &\sum_{i=1}^n \frac{x_i - \hat\mu}{\hat\sigma^2} = 0\\ &\sum_{i=1}^n \left(\frac{(x_i - \hat\mu)^2}{2(\hat\sigma^2)^2} - \frac{1}{2\hat\sigma^2}\right) = 0 \end{align*} \]

つまり，

\[ \begin{align*} &\sum_{i=1}^n(x_i - \hat\mu) = 0\\ &\sum_{i=1}^n[(x_i - \hat\mu)^2 - \hat\sigma^2] = 0 \end{align*} \]

これをM-estimatorと対応させるならば，\(\rho(x_i; \theta) = -\log(\phi(x_i))\) と尤度に基づいたロス関数を用いた問題と理解できます．

また，\(\mu\) に焦点をあてるならば，推定量は核関数が \(\varphi(x; \theta)= x-\mu\) となります． 核関数の形状より，データ \(x\) が非常に大きくなると，核関数 \(\varphi(x; \theta)\) も非常に大きくなってしまいます． 結果として，外れ値 \(x_{outlier}\) が存在すると，M推定量が一つの \(\varphi(x_{outlier}; \theta)\) に振り回されてしまい， ロバスト推定にならないことがわかります．

平均の推定と核関数の形状

import numpy as np
from regmonkey_style import stylewizard as sw

sw.set_templates("regmonkey_line")
np.random.seed(42)

mu, sigma = 0, 1 # mean and standard deviation
X_0 = np.random.normal(mu, sigma, 1000)
X_1 = np.append(X_0, [100, 200, 50])

print(
    """X_0: sample mean = {:.2f}, median = {:.2f}\nX_1: sample mean = {:.2f}, median = {:.2f}
      """.format(
        np.mean(X_0), np.median(X_0), np.mean(X_1), np.median(X_1)
    )
)

X_0: sample mean = 0.02, median = 0.03
X_1: sample mean = 0.37, median = 0.03
      

というOutlier混入データ X_1 について，核関数の形状をコントロールするとどのように推定されるのか確認していきます．

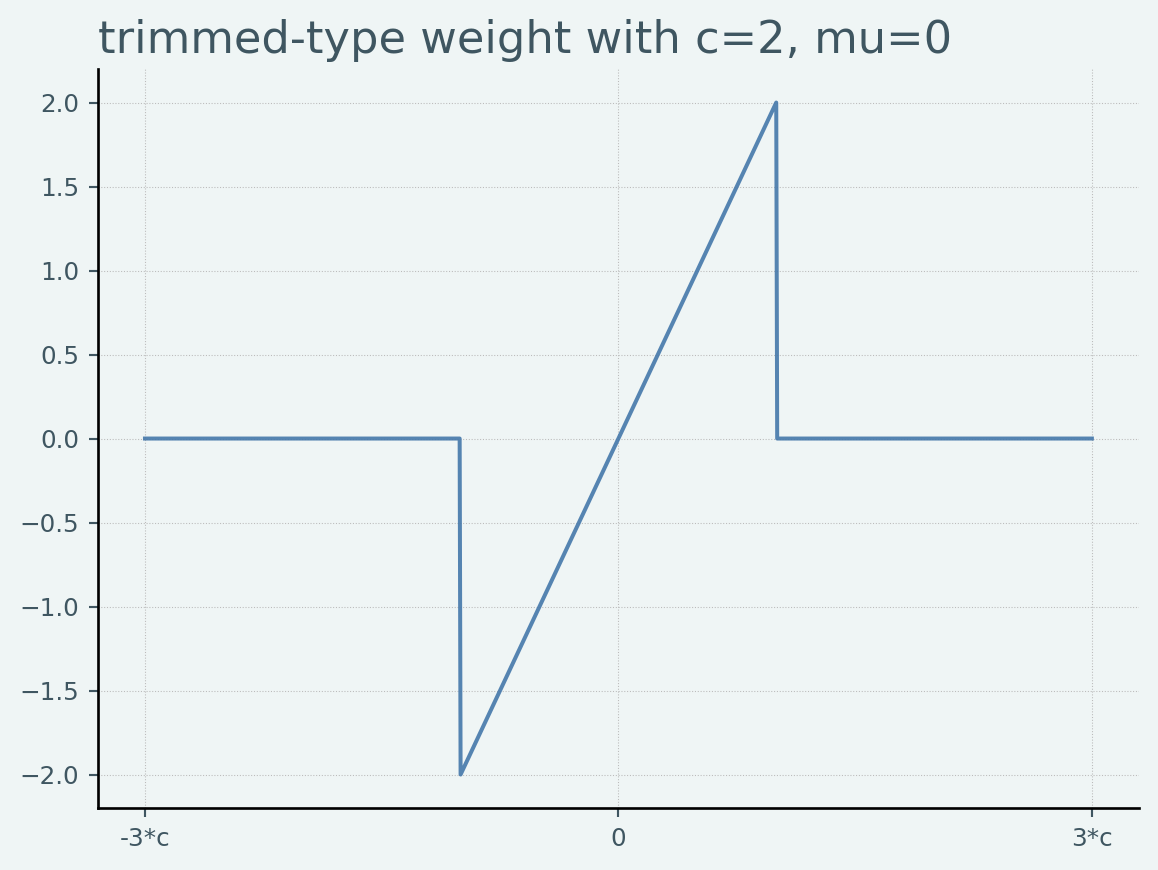
刈り込み型

\[ \varphi(x-\mu) = \left\{\begin{array}{c} x - \mu & \vert x-\mu\vert \leq c\\ 0 & \vert x-\mu\vert > c \end{array}\right. \]

という核関数を刈り込み型(trimmed type)と呼びます． ある閾値 \(c\) 以上のデータは使用しないことを意味し，刈り込み型平均の計算と対応します．

from scipy import stats
import statsmodels.api as sm
import matplotlib.pyplot as plt

## plot func
def plot_weights(support, weights_func, xlabels, xticks, title):
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(support, support * weights_func(support))
    ax.set_xticks(xticks)
    ax.set_xticklabels(xlabels)
    ax.set_title(title)
    return ax

## M-estimator instance
norms = sm.robust.norms

## 可視化
c = 2
support = np.linspace(-3 * c, 3 * c, 1000)
trimmed = norms.TrimmedMean(c=c)
plot_weights(support, trimmed.weights, ["-3*c", "0", "3*c"], [-3 * c, 0, 3 * c], title='trimmed-type weight with c=2, mu=0')

▶  Pythonでの推定

from plotly import express as px

def fit_trimmed_mean(c):
    return (
        sm.RLM(X_1, np.ones(len(X_1)), sm.robust.norms.TrimmedMean(c)).fit().params[0]
    )


c_range = np.linspace(0.01, 200, 50)
robust_means = list(map(fit_trimmed_mean, c_range))
fig = px.line(
    x=c_range,
    y=robust_means,
    markers="x",
    title='trimmed robust regressioon',
    labels={'x': 'c-values', 'y':'estimated mean'}
)
fig.show()

X_1 のうち，outliers [100, 200, 50] を除去した平均が \(0.02\), outliers込の平均が \(0.37\) であることを考えると，適切な \(c\) の設定によって，outlier-robustな平均の推定ができています．また，cのレベルに応じて，loss functionで考慮されるサンプルが増えていくのは刈り込み平均の水準変化と対応していることがわかります．

一方，数値計算上小さすぎるcを選択すると，何も除去されていない平均が推定値として返されてしまっている点に注意が必要です．

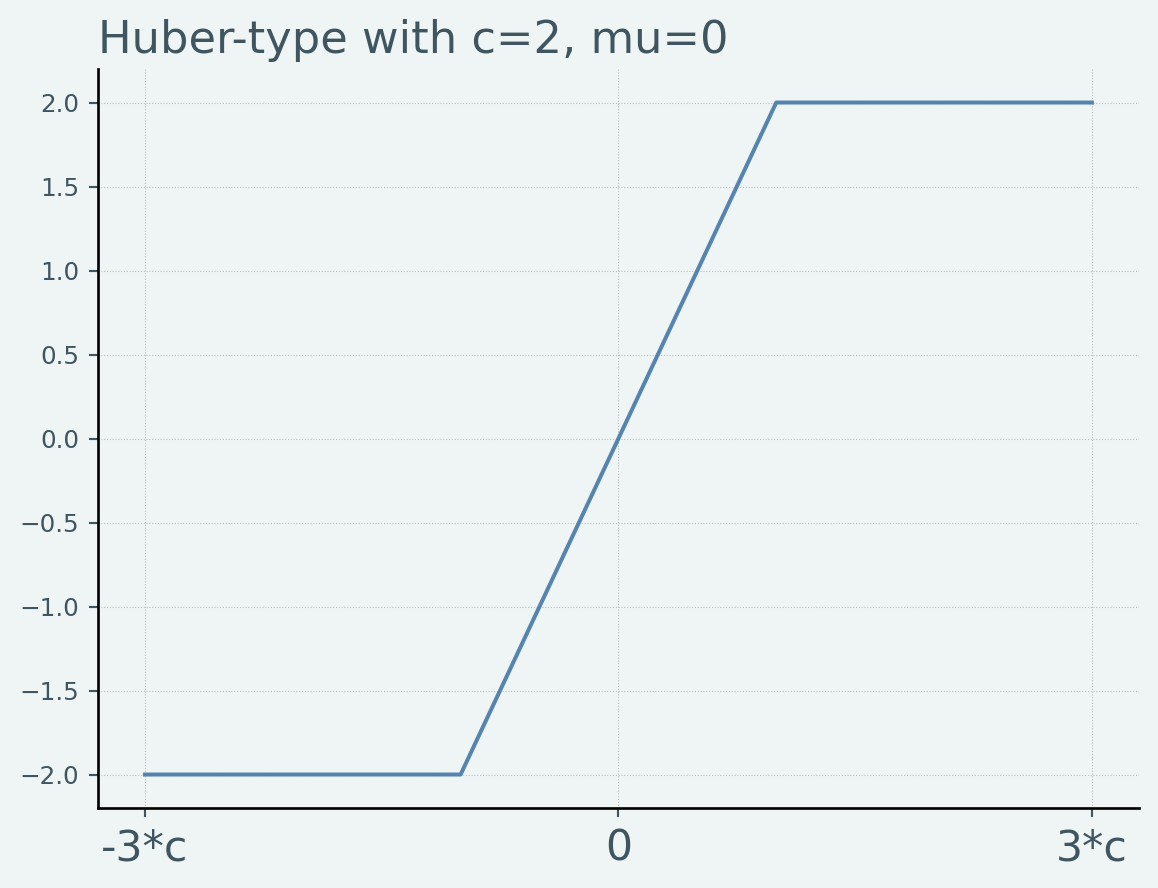
フーバー型

\[ \varphi(x-\mu) = \left\{\begin{array}{c} -c & x -\mu < -c\\ x - \mu & \vert x-\mu\vert \leq c\\ c & x-\mu > c \end{array}\right. \]

という核関数をフーバー型と呼びます．閾値 \(c\) より離れたデータを全く使わない刈り込み型と比べ，影響度は弱めるがある程度は使うことを意図した核関数といえます．フーバー型は凸最適化の解になるので，推定値を得やすいという利点があります．

ただし，

\[ \lim_{\vert x\vert\to\infty}\varphi(x) \neq 0 \]

であるので，Outlierの影響が必ずしもゼロになるわけではない = 最降下(redescending)の性質を持たない点に注意してください．

## 可視化
c = 2
support = np.linspace(-3 * c, 3 * c, 1000)
huber_type = np.clip(support, -c, c)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(support, huber_type)
ax.set_xticks([-3 * c, 0, 3 * c],)
ax.set_xticklabels(["-3*c", "0", "3*c"], fontsize=16)
ax.set_title('Huber-type with c=2, mu=0')
plt.show()

▶  Pythonでの推定

def fit_huber_mean(c):
    return (
        sm.RLM(X_1, np.ones(len(X_1)), sm.robust.norms.HuberT(t=c)).fit().params[0]
    )


c_range = np.linspace(0.01, 200, 50)
robust_means = list(map(fit_huber_mean, c_range))
fig = px.line(
    x=c_range,
    y=robust_means,
    markers="x",
    title='Huber type robust regressioon',
    labels={'x': 'c-values', 'y':'estimated mean'}
)
fig.show()

trimmed mean regressionと比べ，滑らかな推定曲線となっています．cの水準の設定に応じてoutlierの影響が弱められていますが，少なからず影響が残ってしまう点に注意してください．

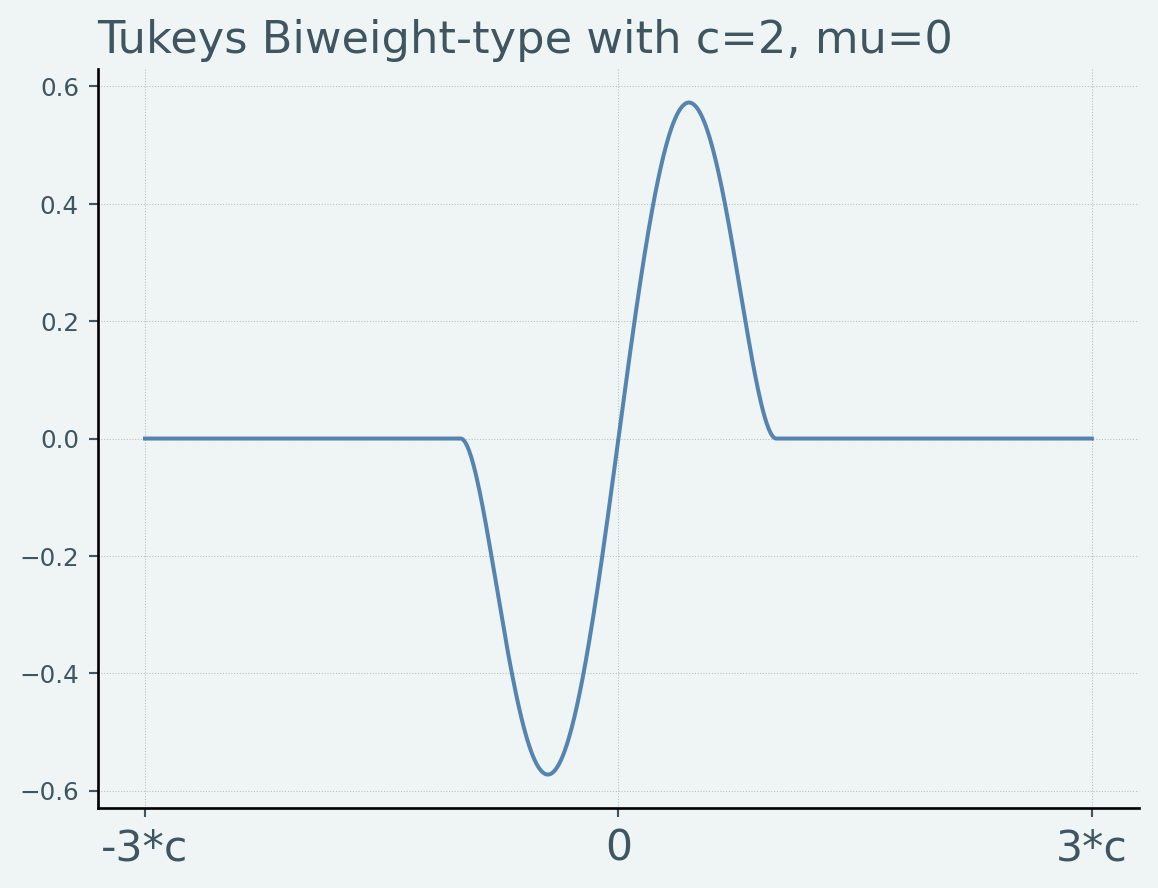
Tukey’s Biweight型

\[ \varphi(x-\mu) = \left\{\begin{array}{c} (x-\mu)\left\{1 - \left(\frac{x-\mu}{c}\right)^2\right\}^2 & \vert x - \mu \vert \leq c\\ 0 & \vert x - \mu \vert > c \end{array}\right. \]

という核関数をTukey’s Biweight型と呼びます．平均 \(\mu\) から離れていくと，核関数の関与が段々と増えていき，あるところからは減り，最終的には 0 になるという性質があります．つまり，最降下の性質を持つ核関数です．

望ましい性質をもっているので，非常によく使われる核関数です．

def tukeys_biweight(x, mu, c):
    x2 = np.clip(x-mu, -c, c)
    return x2 * (1 - (x2/c)**2) ** 2

## 可視化
c = 2
support = np.linspace(-3 * c, 3 * c, 1000)
tukey_kernel = tukeys_biweight(support, 0, c)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(support, tukey_kernel)
ax.set_xticks([-3 * c, 0, 3 * c],)
ax.set_xticklabels(["-3*c", "0", "3*c"], fontsize=16)
ax.set_title('Tukeys Biweight-type with c=2, mu=0')
plt.show()

▶  Pythonでの推定

def fit_tukeysbiwieght_mean(c):
    return (
        sm.RLM(X_1, np.ones(len(X_1)), sm.robust.norms.TukeyBiweight(c=c)).fit().params[0]
    )


c_range = np.linspace(0.01, 200, 50)
robust_means = list(map(fit_tukeysbiwieght_mean, c_range))
fig = px.line(
    x=c_range,
    y=robust_means,
    markers="x",
    title='tukeys biwieght type robust regressioon',
    labels={'x': 'c-values', 'y':'estimated mean'}
)
fig.show()

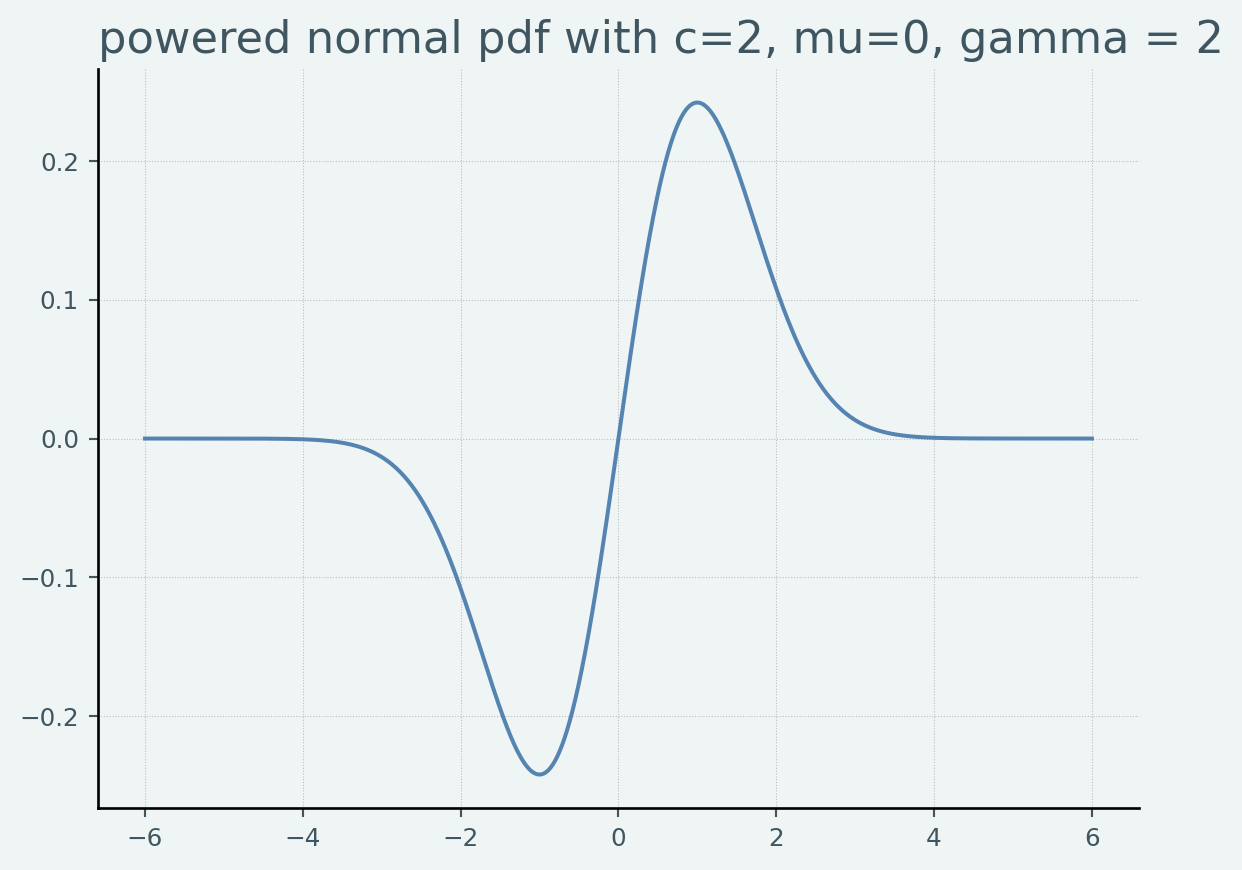
重み付き型

正規分布の密度関数のベキ乗 \(\phi(x_i;\mu,\sigma)^\gamma, (\gamma > 0)\) を重みとして核関数を表現すると

\[ \varphi(x-\mu) = \phi(x_i;\mu,\theta)^\gamma(x-\mu) \]

\(x\) よりも \(\exp(-x^2)\) のほうが早く 0 に近づくので，\(\lim_{x\to\infty} \phi(x_i;\mu,\sigma)^\gamma(x-\mu) = 0\) という性質を持っており，Outlierに強い推定が期待できます．標準偏差 \(\sigma\) については，正規化された中央絶対偏差 \(\operatorname{MADN}\) などがよく使われます．

実際に計算する場合は, \(\sigma_{MADN}\) をMADNとすると

\[ \varphi(x-\mu) = \frac{\phi(x_i;\mu,\sigma_{MADN})^\gamma}{\sum_{i=1}^n \phi(x_i;\mu,\sigma_{MADN})^\gamma}(x-\mu) \]

という形になります．

from scipy.stats import norm

def norml_power_weight(x, mu, sigma, gamma):
    weight = norm.pdf(x, mu, sigma) ** gamma
    return weight * (x - mu) 

## 可視化
c = 2
support = np.linspace(-3 * c, 3 * c, 1000)
normal_power_kernel = norml_power_weight(support, 0, 1, 1)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(support, normal_power_kernel)
ax.set_title('powered normal pdf with c=2, mu=0, gamma = 2')
plt.show()

尤度型

from statsmodels.miscmodels.tmodel import TLinearModel

stats_tmodel = TLinearModel(X_1, np.ones(len(X_1))).fit()
print(stats_tmodel.params[0])

running Tmodel initialize
Optimization terminated successfully.
         Current function value: 1.481456
         Iterations: 127
         Function evaluations: 236
0.006243405777405073